ทฤษฎีบทเบย์อธิบายพร้อมตัวอย่าง – คู่มือฉบับสมบูรณ์

บทนำ

ทฤษฎีบทเบย์คืออะไร?

ทฤษฎีบทของเบย์ใช้สำหรับการคำนวณความน่าจะเป็นแบบมีเงื่อนไขซึ่งสัญชาตญาณมักจะล้มเหลว แม้ว่าจะใช้กันอย่างแพร่หลายในความน่าจะเป็น แต่ทฤษฎีบทก็ถูกนำไปใช้ในด้านการเรียนรู้ของเครื่องด้วย การใช้งานในการเรียนรู้ของเครื่องรวมถึงการปรับโมเดลเข้ากับชุดข้อมูลการฝึกอบรมและการพัฒนาโมเดลการจัดหมวดหมู่

ความน่าจะเป็นแบบมีเงื่อนไขคืออะไร?

ความน่าจะเป็นแบบมีเงื่อนไขมักจะถูกกำหนดให้เป็นความน่าจะเป็นของเหตุการณ์หนึ่งเมื่อเกิดเหตุการณ์อื่น

• ถ้า A และ B เป็นสองเหตุการณ์ ความน่าจะเป็นแบบมีเงื่อนไขของฉันจะถูกกำหนดให้เป็น P(A ที่กำหนด B) หรือ P(A|B)
• ความน่าจะเป็นแบบมีเงื่อนไขสามารถคำนวณได้จากความน่าจะเป็นร่วมกัน (A | B) = P(A, B) / P(B)

• ความน่าจะเป็นแบบมีเงื่อนไขไม่สมมาตร ตัวอย่างเช่น P(A | B) != P(B | A)

วิธีอื่นๆ ในการคำนวณความน่าจะเป็นแบบมีเงื่อนไขรวมถึงการใช้ความน่าจะเป็นแบบมีเงื่อนไขอื่นๆ เช่น

P(A|B) = P(B|A) * P(A) / P(B)

ย้อนกลับยังใช้

P(B|A) = P(A|B) * P(B) / P(A)

วิธีการคำนวณนี้มีประโยชน์เมื่อยากต่อการคำนวณความน่าจะเป็นร่วม มิฉะนั้น เมื่อมีความน่าจะเป็นแบบมีเงื่อนไขย้อนกลับ การคำนวณด้วยวิธีนี้จะกลายเป็นเรื่องง่าย

การคำนวณความน่าจะเป็นแบบมีเงื่อนไขแบบอื่นนี้เรียกว่า Bayes Rule หรือ Bayes Theorem มันถูกตั้งชื่อตามบุคคลที่บรรยายครั้งแรกว่า “สาธุคุณโธมัส เบย์”

สูตรของทฤษฎีบทเบย์

ทฤษฎีบทเบย์เป็นวิธีการคำนวณความน่าจะเป็นแบบมีเงื่อนไขเมื่อไม่มีความน่าจะเป็นร่วมกัน บางครั้ง ตัวส่วนไม่สามารถเข้าถึงได้โดยตรง ในกรณีเช่นนี้ วิธีอื่นในการคำนวณคือ:

P(B) = P(B|A) * P(A) + P(B|ไม่ใช่ A) * P(ไม่ใช่ A)

นี่คือสูตรของทฤษฎีบทเบย์ซึ่งแสดงการคำนวณอื่นของ P(B)

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|ไม่ใช่ A) * P(ไม่ใช่ A)

สูตรข้างต้นสามารถอธิบายได้ด้วยวงเล็บรอบตัวส่วน

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|ไม่ใช่ A) * P(ไม่ใช่ A))

นอกจากนี้ หากเรามี P(A) แล้ว P(ไม่ใช่ A) ก็สามารถคำนวณได้เป็น

P(ไม่ใช่ A) = 1 – P(A)

ในทำนองเดียวกัน ถ้าเรามี P(ไม่ใช่ B|ไม่ใช่ A) ก็สามารถคำนวณ P(B|ไม่ใช่ A) ได้เป็น

P(B|ไม่ใช่ A) = 1 – P(ไม่ใช่ B|ไม่ใช่ A)

ทฤษฎีบทเบย์ของความน่าจะเป็นแบบมีเงื่อนไข

ทฤษฎีบทเบย์ประกอบด้วยคำศัพท์หลายคำซึ่งมีการตั้งชื่อตามบริบทของการประยุกต์ใช้ในสมการ

ความน่าจะเป็นหลังหมายถึงผลลัพธ์ของ P(A|B) และความน่าจะเป็นก่อนหน้าหมายถึง P(A)

• P(A|B): ความน่าจะเป็นภายหลัง
• P(A): ความน่าจะเป็นก่อนหน้า

ในทำนองเดียวกัน P(B|A) และ P(B) จะเรียกว่าความน่าจะเป็นและหลักฐาน

• P(B|A): ความน่าจะเป็น
• P(B): หลักฐาน.

ดังนั้น ทฤษฎีบทเบย์ของความน่าจะเป็นแบบมีเงื่อนไขสามารถปรับปรุงใหม่ได้ดังนี้:

หลัง = โอกาส * ก่อนหน้า / หลักฐาน

หากเราต้องคำนวณความน่าจะเป็นที่จะมีไฟเนื่องจากมีควัน เราจะใช้สมการต่อไปนี้:

P(ไฟ|ควัน) = P(ควัน|ไฟ) * P(ไฟ) / P(ควัน)

โดยที่ P(ไฟ) มาก่อน P(ควัน|ไฟ) คือความน่าจะเป็น และ P(ควัน) เป็นหลักฐาน

ภาพประกอบของทฤษฎีบทเบย์

มีการ อธิบาย ตัวอย่าง ทฤษฎีบทเบย์ เพื่อแสดงการใช้ทฤษฎีบทเบย์ในปัญหา

ปัญหา

มีกล่องสามกล่องที่มีข้อความว่า A B และ C รายละเอียดของกล่องคือ

• กล่อง A ประกอบด้วยลูกบอลสีแดง 2 ลูกและสีดำ 3 ลูก
• กล่อง B ประกอบด้วยลูกบอลสีแดง 3 ลูกและสีดำ 1 ลูก
• และกล่อง C ประกอบด้วยลูกบอลสีแดง 1 ลูกและลูกบอลสีดำ 4 ลูก

ทั้งสามกล่องเหมือนกันโดยมีความน่าจะเป็นเท่ากันที่จะหยิบขึ้นมา ดังนั้นความน่าจะเป็นที่ลูกบอลสีแดงถูกหยิบขึ้นมาจากกล่อง A เป็นเท่าไหร่?

สารละลาย

ให้ E หมายถึงเหตุการณ์ที่หยิบลูกบอลสีแดง และ A, B และ C แสดงว่าหยิบลูกบอลจากกล่องของตน ดังนั้นความน่าจะเป็นแบบมีเงื่อนไขจะเป็น P(A|E) ซึ่งจำเป็นต้องคำนวณ

ความน่าจะเป็นที่มีอยู่ P(A) = P(B) = P (C) = 1 / 3 เนื่องจากกล่องทั้งหมดมีความน่าจะเป็นที่จะถูกหยิบเท่ากัน

P(E|A) = จำนวนลูกสีแดงในกล่อง A / จำนวนลูกในกล่อง A = 2 / 5

ในทำนองเดียวกัน P(E|B) = 3 / 4 และ P(E|C) = 1 / 5

จากนั้นหลักฐาน P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0.45

ดังนั้น P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0.45 = 0.296

ตัวอย่างทฤษฎีบทเบย์

ทฤษฎีบทเบย์ให้ความน่าจะเป็นของ "เหตุการณ์" ด้วยข้อมูลที่กำหนดใน "การทดสอบ"

• มีความแตกต่างระหว่าง "เหตุการณ์" และ "การทดสอบ" เช่น มีการทดสอบโรคตับที่แตกต่างจากการเป็นโรคตับจริง ๆ คือ เหตุการณ์
• เหตุการณ์ที่เกิดขึ้นได้ยากอาจมีอัตราการบวกลวงที่สูงกว่า

ตัวอย่างที่ 1

ความน่าจะเป็นที่ผู้ป่วยจะเป็นโรคตับหากติดสุราเป็นเท่าใด

ในที่นี้ “การเป็นคนติดเหล้า” คือ “การทดสอบ” (การทดสอบสารสีน้ำเงิน) สำหรับโรคตับ

• A คือเหตุการณ์เช่น "ผู้ป่วยเป็นโรคตับ"

ตามบันทึกก่อนหน้านี้ของคลินิกระบุว่า 10% ของผู้ป่วยที่เข้าคลินิกกำลังเป็นโรคตับ

ดังนั้น P(A)=0.10

• B คือการทดสอบสารสีน้ำเงินว่า "ผู้ป่วยติดสุรา"

บันทึกก่อนหน้านี้ของคลินิกพบว่า 5% ของผู้ป่วยที่เข้าคลินิกมีแอลกอฮอล์

ดังนั้น P(B)=0.05

• นอกจากนี้ 7% ของผู้ป่วยที่ได้รับการวินิจฉัยว่าเป็นโรคตับ เป็นผู้ติดสุรา ค่านี้กำหนด B|A: ความน่าจะเป็นของผู้ป่วยที่ติดสุรา เนื่องจากมีโรคตับอยู่ที่ 7%

ตาม สูตรทฤษฎีบทเบ ย์

P(A|B) = (0.07 * 0.1)/0.05 = 0.14

ดังนั้นสำหรับผู้ป่วยที่ติดสุรา โอกาสในการเป็นโรคตับอยู่ที่ 0.14 (14%)

ตัวอย่าง2

• ไฟอันตรายหายาก (1%)
• แต่ควันเป็นเรื่องปกติธรรมดา (10%) เนื่องจากบาร์บีคิว
• และ 90% ของไฟอันตรายทำให้เกิดควัน

ความน่าจะเป็นที่จะเกิดอัคคีภัยเมื่อมีควันเป็นเท่าใด

การคำนวณ

P(ไฟ|ควัน) =P(ไฟ) P(ควัน|ไฟ)/P(ควัน)

= 1% x 90%/10%

= 9%

ตัวอย่างที่ 3

โอกาสที่ฝนตกในตอนกลางวันเป็นอย่างไร? โดยที่ Rain หมายถึงฝนตกในตอนกลางวัน และ Cloud หมายถึงตอนเช้ามีเมฆมาก

โอกาสที่ฝนจะตกมีเมฆเขียนว่า P(ฝน|เมฆ)

P(ฝน|เมฆ) = P(ฝน) P(เมฆ|ฝน)/P(เมฆ)

P(ฝน) คือ ความน่าจะเป็นของฝน = 10%

P(Cloud|Rain) คือ ความน่าจะเป็นของเมฆ โดยที่ Rain เกิดขึ้น = 50%

P(Cloud) คือความน่าจะเป็นของคลาวด์ = 40%

P(ฝน|เมฆ) = 0.1 x 0.5/0.4 = .125

ดังนั้น มีโอกาสเกิดฝน 12.5%

แอปพลิเคชั่น

การประยุกต์ใช้ทฤษฎีบท Bayes หลายอย่างมีอยู่ในโลกแห่งความเป็นจริง การใช้งานหลักบางประการของทฤษฎีบทคือ:

1. การสร้างแบบจำลองสมมติฐาน

ทฤษฎีบท Bayes พบการประยุกต์ใช้อย่างกว้างขวางในการเรียนรู้ของเครื่องที่นำไปใช้ และสร้างความสัมพันธ์ระหว่างข้อมูลกับแบบจำลอง แมชชีนเลิร์นนิงประยุกต์ใช้กระบวนการทดสอบและวิเคราะห์สมมติฐานต่างๆ ในชุดข้อมูลที่กำหนด

เพื่ออธิบายความสัมพันธ์ระหว่างข้อมูลกับแบบจำลอง ทฤษฎีบทเบย์ได้จัดเตรียมแบบจำลองความน่าจะเป็น

P(h|D) = P(D|h) * P(h) / P(D)

ที่ไหน,

P(h|D): ความน่าจะเป็นหลังของสมมติฐาน

P(h): ความน่าจะเป็นก่อนหน้าของสมมติฐาน

การเพิ่มขึ้นของ P(D) จะทำให้ค่า P(h|D) ลดลง ในทางกลับกัน หาก P(h) และความน่าจะเป็นของการสังเกตข้อมูลที่ให้สมมติฐานเพิ่มขึ้น ความน่าจะเป็นของ P(h|D) จะเพิ่มขึ้น

2. ทฤษฎีบทเบย์สำหรับการจำแนกประเภท

วิธีการจัดประเภทเกี่ยวข้องกับการติดฉลากของข้อมูลที่กำหนด สามารถกำหนดเป็นการคำนวณความน่าจะเป็นแบบมีเงื่อนไขของป้ายชื่อคลาสที่ได้รับตัวอย่างข้อมูล

P(คลาส|ข้อมูล) = (P(ข้อมูล|คลาส) * P(คลาส)) / P(ข้อมูล)

โดยที่ P(class|data) คือความน่าจะเป็นของคลาสที่ได้รับจากข้อมูลที่ให้มา

การคำนวณสามารถทำได้สำหรับแต่ละชั้นเรียน คลาสที่มีความน่าจะเป็นมากที่สุดสามารถกำหนดให้กับข้อมูลที่ป้อนได้

การคำนวณความน่าจะเป็นแบบมีเงื่อนไขไม่สามารถทำได้ภายใต้เงื่อนไขของตัวอย่างจำนวนน้อย ดังนั้นการประยุกต์ใช้ทฤษฎีบทเบย์โดยตรงจึงไม่สามารถทำได้ วิธีแก้ปัญหาสำหรับแบบจำลองการจัดประเภทอยู่ในการคำนวณแบบง่าย

• Naive Bayes ลักษณนาม

ทฤษฎีบทเบย์ถือว่าตัวแปรอินพุตขึ้นอยู่กับตัวแปรอื่นซึ่งทำให้การคำนวณมีความซับซ้อน ดังนั้น สมมติฐานจะถูกลบออกและทุกตัวแปรอินพุตถือเป็นตัวแปรอิสระ ด้วยเหตุนี้ โมเดลจึงเปลี่ยนจากโมเดลความน่าจะเป็นแบบมีเงื่อนไขขึ้นอยู่กับอิสระ ในที่สุดก็ลดความซับซ้อนลง

การทำให้เข้าใจง่ายของทฤษฎีบทเบย์นี้เรียกว่าอ่าวไร้เดียงสา มีการใช้กันอย่างแพร่หลายสำหรับการจัดหมวดหมู่และการทำนายแบบจำลอง

• Bayes Optimal Classifier

นี่คือแบบจำลองความน่าจะเป็นประเภทหนึ่งที่เกี่ยวข้องกับการคาดคะเนตัวอย่างใหม่ที่ได้รับจากชุดข้อมูลการฝึกอบรม ตัวอย่างหนึ่งของ Bayes Optimal Classifier คือ “การจำแนกประเภทที่น่าจะเป็นไปได้มากที่สุดของอินสแตนซ์ใหม่จากข้อมูลการฝึกคืออะไร”

การคำนวณความน่าจะเป็นแบบมีเงื่อนไขของอินสแตนซ์ใหม่จากข้อมูลการฝึกสามารถทำได้โดยใช้สมการต่อไปนี้

P(vj | D) = ผลรวม {h ใน H} P(vj | hi) * P(hi | D)

โดยที่ vj เป็นอินสแตนซ์ใหม่ที่จะจัดประเภท

H คือเซตของสมมติฐานสำหรับการจำแนกอินสแตนซ์

สวัสดีเป็นสมมติฐานที่กำหนด

P(vj | hi) คือความน่าจะเป็นหลังของ vi จากสมมติฐาน hi และ

P(hi | D) คือความน่าจะเป็นหลังของสมมติฐาน hi จากข้อมูล D

3. การใช้ทฤษฎีบทเบย์ในการเรียนรู้ของเครื่อง

การประยุกต์ใช้ทฤษฎีบท Bayes ที่พบบ่อยที่สุดในการเรียนรู้ของเครื่องคือการพัฒนาปัญหาการจำแนกประเภท แอปพลิเคชันอื่นๆ ที่มากกว่าการจัดหมวดหมู่นั้นรวมถึงการเพิ่มประสิทธิภาพและแบบจำลองทั่วไป

• การเพิ่มประสิทธิภาพแบบเบย์

เป็นงานที่ท้าทายเสมอในการค้นหาข้อมูลที่ส่งผลให้ต้นทุนต่ำสุดหรือสูงสุดของฟังก์ชันวัตถุประสงค์ที่กำหนด การเพิ่มประสิทธิภาพ Bayesian ขึ้นอยู่กับทฤษฎีบท Bayes และให้แง่มุมสำหรับการค้นหาปัญหาการปรับให้เหมาะสมทั่วโลก วิธีการนี้รวมถึงการสร้างแบบจำลองความน่าจะเป็น (ฟังก์ชันตัวแทน) การค้นหาผ่านฟังก์ชันการได้มา และการเลือกตัวอย่างตัวเลือกสำหรับการประเมินฟังก์ชันวัตถุประสงค์จริง

ในแมชชีนเลิร์นนิงที่ประยุกต์ใช้ การเพิ่มประสิทธิภาพแบบเบย์ใช้เพื่อปรับแต่งไฮเปอร์พารามิเตอร์ของโมเดลที่มีประสิทธิภาพดี

• เครือข่ายความเชื่อแบบเบย์

ความสัมพันธ์ระหว่างตัวแปรอาจกำหนดได้โดยใช้แบบจำลองความน่าจะเป็น พวกเขายังใช้สำหรับการคำนวณความน่าจะเป็น แบบจำลองความน่าจะเป็นแบบมีเงื่อนไขทั้งหมดอาจไม่สามารถคำนวณความน่าจะเป็นได้เนื่องจากมีข้อมูลจำนวนมาก Naive Bayes ทำให้วิธีการคำนวณง่ายขึ้น ยังมีอีกวิธีหนึ่งที่แบบจำลองได้รับการพัฒนาบนพื้นฐานของการพึ่งพาอาศัยกันแบบมีเงื่อนไขที่ทราบระหว่างตัวแปรสุ่มและความเป็นอิสระตามเงื่อนไขในกรณีอื่นๆ เครือข่ายแบบเบย์จะแสดงการพึ่งพาและความเป็นอิสระนี้ผ่านแบบจำลองกราฟความน่าจะเป็นที่มีขอบตรง การขึ้นต่อกันแบบมีเงื่อนไขที่ทราบจะแสดงเป็นขอบตรง และการเชื่อมต่อที่ขาดหายไปแสดงถึงความเป็นอิสระแบบมีเงื่อนไขในแบบจำลอง

4. การกรองสแปมแบบเบย์

การกรองสแปมเป็นอีกหนึ่งการประยุกต์ใช้ทฤษฎีบทเบย์ มีเหตุการณ์สองเหตุการณ์:

• เหตุการณ์ A: ข้อความเป็นสแปม
• ทดสอบ X: ข้อความมีคำบางคำ (X)

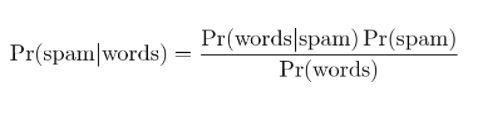
ด้วยการประยุกต์ใช้ทฤษฎีบท Bayes จะสามารถคาดการณ์ได้ว่าข้อความนั้นเป็นสแปมหรือไม่เมื่อได้รับ "ผลการทดสอบ" การวิเคราะห์คำในข้อความสามารถคำนวณโอกาสในการเป็นข้อความสแปม ด้วยการฝึกอบรมตัวกรองที่มีข้อความซ้ำ ๆ การปรับปรุงข้อเท็จจริงที่ว่าความน่าจะเป็นที่จะมีคำบางคำในข้อความจะเป็นสแปม

การประยุกต์ใช้ทฤษฎีบทเบย์พร้อมตัวอย่าง

ผู้ผลิตตัวเร่งปฏิกิริยาผลิตอุปกรณ์สำหรับทดสอบข้อบกพร่องในตัวเร่งปฏิกิริยาด้วยไฟฟ้า (EC) ผู้ผลิตตัวเร่งปฏิกิริยาอ้างว่าการทดสอบมีความน่าเชื่อถือ 97% หาก EC มีข้อบกพร่องและเชื่อถือได้ 99% เมื่อไม่มีที่ติ อย่างไรก็ตาม 4% ของ EC ดังกล่าวอาจคาดว่าจะมีข้อบกพร่องเมื่อส่งมอบ กฎของเบย์ถูกนำมาใช้เพื่อตรวจสอบความน่าเชื่อถือที่แท้จริงของอุปกรณ์ ชุดเหตุการณ์พื้นฐานคือ

A : EC มีข้อบกพร่อง; A': EC ไม่มีที่ติ; B: EC ได้รับการทดสอบว่ามีข้อบกพร่อง B': EC ได้รับการทดสอบแล้วว่าไม่มีที่ติ

ความน่าจะเป็นจะเป็น

B/A: EC คือ (ทราบว่า) เสีย และทดสอบแล้วว่าเสีย P(B/A) = 0.97,

B'/A: EC (ทราบว่า) มีข้อบกพร่อง แต่ทดสอบแล้วไม่มีที่ติ P(B'/A)=1-P(B/A)=0.03,

B/A': EC คือ (ทราบว่า) เสีย แต่ทดสอบแล้วว่าเสีย P(B/A') = 1- P(B'/A')=0.01

B'/A: = EC คือ (ที่รู้กันว่า) ไร้ที่ติ และผ่านการทดสอบไร้ที่ติ P(B'/A') = 0.99

ความน่าจะเป็นที่คำนวณโดยทฤษฎีบทเบย์คือ:

ความน่าจะเป็นของการคำนวณแสดงให้เห็นว่ามีความเป็นไปได้สูงที่จะปฏิเสธ EC ที่ไร้ตำหนิ (ประมาณ 20%) และมีความเป็นไปได้น้อยที่จะระบุ EC ที่บกพร่อง (ประมาณ 80%)

บทสรุป

คุณลักษณะที่โดดเด่นที่สุดประการหนึ่งของทฤษฎีบทเบย์คือจากอัตราส่วนความน่าจะเป็นเพียงไม่กี่อัตรา สามารถรับข้อมูลจำนวนมหาศาลได้ ด้วยวิธีความน่าจะเป็น ความน่าจะเป็นของเหตุการณ์ก่อนหน้าสามารถเปลี่ยนเป็นความน่าจะเป็นภายหลังได้ แนวทางของทฤษฎีบทเบย์สามารถนำไปใช้ในด้านสถิติ ญาณวิทยา และตรรกะอุปนัย

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับ Bayes Theorem, AI และแมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's Executive PG Program ใน Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง มากกว่า 30 กรณี การศึกษาและการมอบหมายงาน, สถานะศิษย์เก่า IIIT-B, โครงการหลักที่ปฏิบัติได้จริงมากกว่า 5 โครงการและความช่วยเหลือด้านงานกับบริษัทชั้นนำ