Что такое байесовское мышление? Введение и теорема

Статистическая теорема, сформулированная английским статистиком и философом Томасом Байесом в 1700-х годах, продолжает оставаться путеводной звездой для ученых и аналитиков во всем мире. Сегодня байесовское мышление находит применение в медицине, науке, технике и некоторых других дисциплинах и продолжает сильно влиять на наше мировоззрение и результирующие действия.

Идея Томаса Байеса была поразительно проста. Согласно Байесу, вероятность того, что гипотеза верна, зависит от двух условий: насколько она обоснована на том, что мы уже знаем (априорные знания), и насколько хорошо она соответствует новым данным. Таким образом, байесовское мышление отличается от традиционной проверки гипотез тем, что первое включает предварительное знание, прежде чем делать поспешные выводы.

Имея в виду предварительное введение, давайте более подробно рассмотрим байесовскую статистику.

Байесовская статистика

Проще говоря, байесовская статистика применяет вероятности к статистическим задачам для обновления предыдущих убеждений в свете новых данных. Вероятность выражает степень уверенности в конкретном событии.

Степень уверенности может быть основана на предыдущих знаниях о событии, основанных на личных предположениях или результатах предыдущих экспериментов. Байесовская статистика использует теорему Байеса для вычисления вероятностей. Теорема Байеса, в свою очередь, описывает условную вероятность события на основе новых данных и предшествующей информации, связанной с событием.

Имея это в виду, давайте освежим в памяти фундаментальную концепцию условной вероятности, прежде чем мы углубимся в теорему Байеса.

Условная возможность

Условная вероятность может быть определена как вероятность события или результата, основанная на возникновении предыдущего события или результата. Он рассчитывается путем умножения вероятности предшествующего события на вероятность последующего или условного события.

Давайте рассмотрим пример, чтобы лучше понять концепцию .

• Событие А заключается в том, что семья, планирующая прогулку, отправляется на пикник. Вероятность того, что семья поедет на пикник, составляет 80%.
• Событие Б состоит в том, что в тот день, когда семья отправится на пикник, пойдет дождь. Прогноз погоды говорит, что вероятность осадков в день пикника составляет 60%.
• Следовательно, вероятность (P) того, что семья поедет на пикник и пойдет дождь, вычисляется следующим образом:

P (Пикник и дождь) = P (Дождь | Пикник) P (Пикник) = (0,60) * (0,80) = 0,48

В приведенном выше примере условная вероятность рассматривает два события A и B во взаимосвязи друг с другом, то есть вероятность того, что семья пойдет на пикник и в тот же день пойдет дождь.

Следовательно, условная вероятность отличается от безусловной вероятности, поскольку последняя относится к вероятности возникновения события независимо от того, произошло ли какое-либо другое событие или события или присутствуют какие-либо другие условия.

Формула условной вероятности

Формула условной вероятности исходит из правила умножения вероятности:

P (A и B) или P (AUB) = P (B при заданном A) или P (B | A) * P (A)

В приведенном выше уравнении P (A и B) — это совместная вероятность, относящаяся к вероятности одновременного возникновения двух или более событий. Это также пишется как P (A, B).

Вот как вывести уравнение условной вероятности из правила умножения:

Шаг 1: Запишите правило умножения.

Р (А и В) = Р (В | А) * Р (А)

Шаг 2: Разделите обе части уравнения на P (A).

Р (А и В) / Р (А) = Р (В | А) * Р (А) / Р (А)

Шаг 3: Отмените P (A) в правой части уравнения.

Р (А и В) / Р (А) = Р (В | А)

Шаг 4: Перепишите уравнение.

Р(А и В) = Р(В|А)/Р(А)

Таким образом, формула условной вероятности имеет вид:

Р(А и В) = Р(В|А)/Р(А)

Теорема Байеса

Используя теорему Байеса, мы можем обновить наши убеждения и убеждения, основываясь на новых и релевантных доказательствах. Например, если мы пытаемся вычислить вероятность того, что данный человек болен раком, мы обычно предполагаем, что это процент населения, больного раком. Однако, если мы введем дополнительные доказательства, например, рассматриваемый человек является постоянным курильщиком, мы можем обновить наше восприятие (и, следовательно, вероятность), поскольку вероятность заболевания раком выше, если человек является курильщиком. Следовательно, мы используем как наши предварительные знания, так и дополнительные доказательства, чтобы улучшить наши оценки.

Формула теоремы Байеса

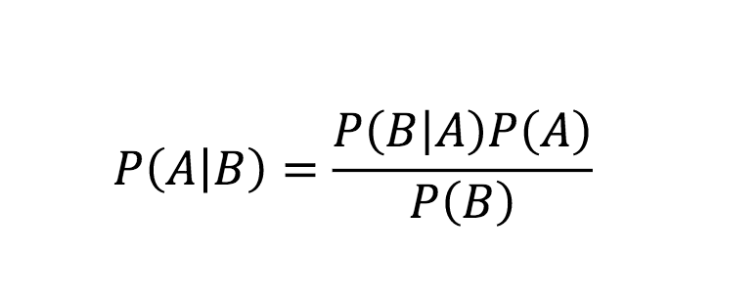
Источник

Приведенное выше уравнение является правилом Байеса. Теперь давайте рассмотрим пошаговый вывод уравнения теоремы Байеса.

Шаг 1: Рассмотрим два события, А и В. А — это событие, вероятность которого мы хотим рассчитать, а В — дополнительное свидетельство, связанное с А.

Шаг 2: Запишите связь между совместной вероятностью и условной вероятностью событий A и B.

Р (А, В) = Р (А | В) * Р (В) = Р (В, А) = Р (В | А) * Р (А)

Шаг 3: Установите два условия условной вероятности равными друг другу.

Р (А | В) * Р (В) = Р (В | А) * Р (А)

Шаг 4: Разделите обе части уравнения на P (B).

Р (А | В) * Р (В) / Р (В) = Р (В | А) * Р (А) / Р (В)

Шаг 5: Отмените P (B) в левой части уравнения.

Р (А | В) = Р (В | А) * Р (А) / Р (В)

Таким образом, мы получаем формулу теоремы Байеса следующим образом:

Р (А | В) = Р (В | А) * Р (А) / Р (В)

Понимание терминов в уравнении теоремы Байеса

Р (А | В) = Р (В | А) * Р (А) / Р (В)

• P(A|B) называется апостериорной вероятностью или вероятностью, которую мы пытаемся оценить. Основываясь на предыдущем примере, апостериорная вероятность будет вероятностью того, что у человека рак, при условии, что этот человек регулярно курит.
• P (B | A) называется правдоподобием , имея в виду вероятность обнаружения дополнительных свидетельств с учетом нашей исходной гипотезы. В приведенном выше примере вероятность — это вероятность того, что человек курит, при условии, что у него рак.
• P(A) — априорная вероятность или вероятность нашей гипотезы без каких-либо дополнительных доказательств или информации. В приведенном выше примере априорная вероятность — это вероятность наличия рака.
• P(B) — предельная вероятность или общая вероятность наблюдения свидетельства. В контексте приведенного выше примера предельная вероятность — это вероятность быть курильщиком.

Простой пример для понимания теоремы Байеса

Используя некоторые гипотетические числа в предыдущем примере, мы увидим эффект применения теоремы Байеса.

Предположим, что вероятность заболеть раком равна 0,06, то есть 6% людей болеют раком. Теперь предположим, что вероятность быть курильщиком составляет 0,20, или 20% людей курят, а 30% людей, больных раком, курят. Итак, P (Курильщик | Рак) = 0,30.

Изначально вероятность заболеть раком составляет просто 0,06 (ранее). Но, используя новые данные, мы можем рассчитать P (Рак | Курильщик) = P ((Курильщик | Рак) * P (Рак)) / P (Курильщик) = (0,30 * 0,06) / (0,20) = 0,09.

Изучайте онлайн- курсы по науке о данных в лучших университетах мира. Участвуйте в программах Executive PG, Advanced Certificate Programs или Master Programs, чтобы ускорить свою карьеру.

Путь вперед: освойте концепции статистики для карьеры в науке о данных или машинном обучении

Учебная платформа upGrad для высших учебных заведений EdTech оказала влияние на более чем 500 000 работающих профессионалов по всему миру благодаря множеству курсов и иммерсивному обучению. С более чем 40 000 слушателей в более чем 85 странах отраслевые курсы upGrad гарантированно помогут вам продвинуться по карьерной лестнице в выбранной вами области.

Магистр наук в области науки о данных - это 18-месячный курс, в ходе которого приобретаются ключевые навыки в области статистики, прогнозного анализа, машинного обучения, аналитики больших данных, визуализации данных и т. д.

Основные моменты программы:

• Степень магистра в Ливерпульском университете Джона Мура и Executive PGP в IIIT Bangalore.
• Более 500 часов контента, более 60 тематических исследований и проектов, более 20 живых сессий, более 14 языков и инструментов программирования.
• Отраслевые сети, сеансы разрешения сомнений и поддержка обучения

Расширенная программа сертификации в области машинного обучения и глубокого обучения — это строгий 6-месячный курс с возможностями для общения с коллегами, практическими проектами, отраслевым наставничеством и всесторонней помощью в карьере.

Основные моменты программы:

• Престижное признание от IIIT Bangalore
• Более 240 часов контента, более 5 тематических исследований и проектов, более 24 живых сессий, охват 12 языков программирования, инструментов и библиотек.
• Групповые коуч-сессии 1:8 и менторские сессии 1:1 с отраслевыми экспертами

Заключение

Байесовское мышление лежит в основе нескольких областей человеческого мышления, исследований и убеждений, хотя большинство из нас этого не осознает. От скрининга рака и глобального потепления до денежно-кредитной политики , оценки рисков и страхования — байесовское мышление является фундаментальным. Считается, что даже знаменитый британский математик Алан Тьюринг использовал байесовский подход для взлома немецкого кода Enigma во время Второй мировой войны.

Зарегистрируйтесь в upGrad и узнайте больше об основных статистических концепциях и многом другом!