Полиномиальная регрессия: важность, пошаговая реализация

Введение

В этой обширной области машинного обучения, какой алгоритм был бы первым, который большинство из нас изучило бы? Да, это линейная регрессия. В основном, будучи первой программой и алгоритмом, которые можно было бы изучить в первые дни программирования машинного обучения, линейная регрессия имеет собственное значение и силу с линейным типом данных.

Что, если набор данных, с которым мы сталкиваемся, не является линейно разделимым? Что, если модель линейной регрессии не может вывести какую-либо связь между независимыми и зависимыми переменными?

Существует еще один тип регрессии, известный как полиномиальная регрессия. В соответствии со своим названием, полиномиальная регрессия представляет собой алгоритм регрессии, который моделирует взаимосвязь между зависимой переменной (y) и независимой переменной (x) в виде полинома n-й степени. В этой статье мы поймем алгоритм и математику полиномиальной регрессии, а также ее реализацию в Python.

Что такое полиномиальная регрессия?

Как было определено ранее, полиномиальная регрессия — это особый случай линейной регрессии, в котором полиномиальное уравнение с указанной степенью (n) соответствует нелинейным данным, которые образуют криволинейную связь между зависимыми и независимыми переменными.

y= b 0 +b 1 x 1 + b 2 x 1 2 + b 3 x 1 3 +…… b n x 1 n

Здесь,

y - зависимая переменная (выходная переменная)

x1 — независимая переменная (предикторы)

b 0 — смещение

b 1 , b 2 , ….b n — веса в уравнении регрессии.

По мере того, как степень полиномиального уравнения ( n ) становится выше, полиномиальное уравнение становится более сложным, и существует вероятность того, что модель имеет тенденцию к переобучению, что будет обсуждаться в следующей части.

Сравнение уравнений регрессии

Простая линейная регрессия ===> y= b0+b1x

Множественная линейная регрессия ===> y= b0+b1x1+ b2x2+ b3x3+…… bnxn

Полиномиальная регрессия ===> y= b0+b1x1+ b2x12+ b3x13+…… bnx1n

Из приведенных выше трех уравнений мы видим, что в них есть несколько тонких отличий. Простая и множественная линейная регрессия отличаются от уравнения полиномиальной регрессии тем, что имеют степень только 1. Множественная линейная регрессия состоит из нескольких переменных x1, x2 и так далее. Хотя уравнение полиномиальной регрессии имеет только одну переменную x1, оно имеет степень n, которая отличает его от двух других.

Необходимость полиномиальной регрессии

Из приведенных ниже диаграмм видно, что на первой диаграмме линейная линия пытается соответствовать заданному набору нелинейных точек данных. Понятно, что прямой линии становится очень трудно сформировать связь с этими нелинейными данными. Из-за этого, когда мы обучаем модель, функция потерь увеличивается, что приводит к высокой ошибке.

С другой стороны, когда мы применяем полиномиальную регрессию, ясно видно, что линия хорошо соответствует точкам данных. Это означает, что полиномиальное уравнение, которое соответствует точкам данных, устанавливает некоторую связь между переменными в наборе данных. Таким образом, для таких случаев, когда точки данных расположены нелинейным образом, нам требуется модель полиномиальной регрессии.

Реализация полиномиальной регрессии в Python

Отсюда мы построим модель машинного обучения в Python, реализующую полиномиальную регрессию. Мы сравним результаты, полученные с помощью линейной регрессии и полиномиальной регрессии. Давайте сначала разберемся с проблемой, которую мы собираемся решить с помощью полиномиальной регрессии.

описание проблемы

В этом случае рассмотрим случай стартапа, который хочет нанять нескольких кандидатов из компании. В компании есть разные вакансии на разные должности. В стартапе есть подробная информация о зарплате для каждой должности в предыдущей компании. Таким образом, когда кандидат упоминает свою предыдущую зарплату, HR стартапа должен сверить ее с имеющимися данными. Таким образом, у нас есть две независимые переменные: Позиция и Уровень. Зависимая переменная (выход) — это заработная плата , которая должна быть предсказана с использованием полиномиальной регрессии.

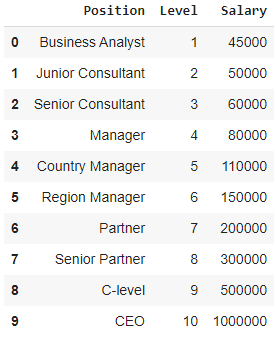
Визуализируя приведенную выше таблицу в виде графика, мы видим, что данные носят нелинейный характер. Другими словами, по мере повышения уровня зарплата увеличивается с большей скоростью, что дает нам кривую, как показано ниже.

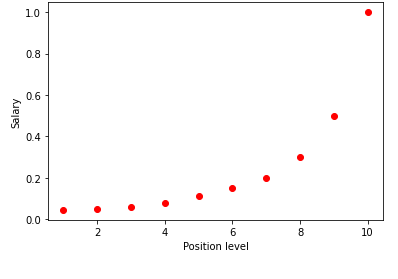
Шаг 1: Предварительная обработка данныхПервым шагом в создании любой модели машинного обучения является импорт библиотек. Здесь у нас есть только три основные библиотеки для импорта. После этого набор данных импортируется из моего репозитория GitHub, и назначаются зависимые переменные и независимые переменные. Независимые переменные хранятся в переменной X, а зависимая переменная хранится в переменной y.

импортировать numpy как np

импортировать matplotlib.pyplot как plt

импортировать панд как pd

набор данных = pd.read_csv('https://raw.githubusercontent.com/mk-gurucharan/Regression/master/PositionSalaries_Data.csv')

X = набор данных.iloc[:, 1:-1].значения

y = набор данных.iloc[:, -1].значения

Здесь в термине [:, 1:-1] первое двоеточие означает, что должны быть взяты все строки, а термин 1:-1 означает, что столбцы, которые должны быть включены, находятся от первого столбца до предпоследнего столбца, который задается выражением -1.

Шаг 2: Модель линейной регрессииНа следующем шаге мы построим модель множественной линейной регрессии и используем ее для прогнозирования данных о заработной плате на основе независимых переменных. Для этого класс LinearRegression импортируется из библиотеки sklearn. Затем он подгоняется к переменным X и y в целях обучения.

из sklearn.linear_model импортировать линейную регрессию

регрессор = линейная регрессия ()

regressor.fit(X, y)

После того, как модель построена, визуализируя результаты, мы получаем следующий график.

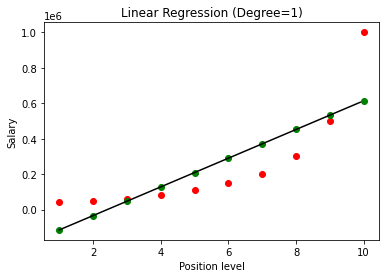
Как ясно видно, при попытке подобрать прямую линию к нелинейному набору данных нет никакой связи, полученной моделью машинного обучения. Таким образом, нам нужно перейти к полиномиальной регрессии, чтобы получить связь между переменными.

Шаг 3: Модель полиномиальной регрессииНа следующем этапе мы подгоним модель полиномиальной регрессии к этому набору данных и визуализируем результаты. Для этого мы импортируем еще один класс из модуля sklearn с именем PolynomialFeatures, в котором мы указываем степень строящегося полиномиального уравнения. Затем класс LinearRegression используется для подгонки полиномиального уравнения к набору данных.

из sklearn.preprocessing импортировать PolynomialFeatures

из sklearn.linear_model импортировать линейную регрессию

poly_reg = PolynomialFeatures (степень = 2)

X_poly = poly_reg.fit_transform(X)

lin_reg = Линейная регрессия()

lin_reg.fit(X_poly, у)

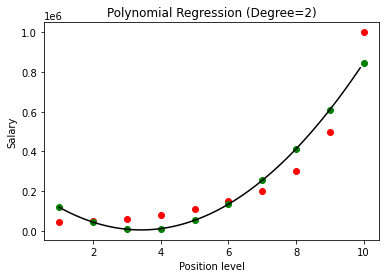
В приведенном выше случае мы задали степень полиномиального уравнения равной 2. При построении графика мы видим, что есть своего рода полученная кривая, но все же есть большое отклонение от реальных данных (красный цвет). ) и прогнозируемые точки кривой (зеленые). Таким образом, на следующем шаге мы увеличим степень многочлена до более высоких чисел, таких как 3 и 4, а затем сравним их друг с другом.

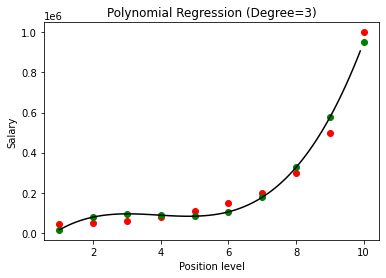
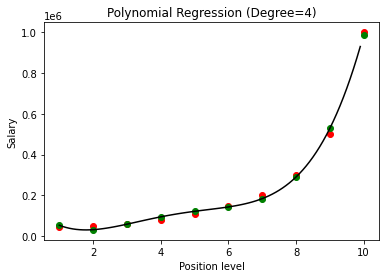
Сравнивая результаты полиномиальной регрессии со степенями 3 и 4, мы видим, что по мере увеличения степени модель хорошо обучается на данных. Таким образом, мы можем сделать вывод, что более высокая степень позволяет полиномиальному уравнению более точно соответствовать обучающим данным. Тем не менее, это идеальный случай переобучения. Таким образом, становится важным выбрать значение n точно, чтобы предотвратить переоснащение.

Что такое переоснащение?

Как следует из названия, переобучением называется ситуация в статистике, когда функция (или в данном случае модель машинного обучения) слишком близко подходит к набору ограниченных точек данных. Это приводит к плохой работе функции с новыми точками данных.

В машинном обучении, если говорят, что модель подходит для заданного набора точек обучающих данных, то, когда та же модель вводится в совершенно новый набор точек (скажем, набор тестовых данных), она очень плохо работает на нем, поскольку модель переобучения плохо обобщала данные и переобучает только точки обучающих данных.

В полиномиальной регрессии есть большая вероятность того, что модель переобучится на обучающих данных по мере увеличения степени полинома. В приведенном выше примере мы видим типичный случай переобучения в полиномиальной регрессии, который можно исправить только методом проб и ошибок для выбора оптимального значения степени.

Читайте также: Идеи проекта машинного обучения

Заключение

В заключение, полиномиальная регрессия используется во многих ситуациях, когда существует нелинейная связь между зависимыми и независимыми переменными. Хотя этот алгоритм страдает чувствительностью к выбросам, его можно исправить, обработав их перед подбором линии регрессии. Таким образом, в этой статье мы познакомились с концепцией полиномиальной регрессии вместе с примером ее реализации в программировании на Python для простого набора данных.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, 5+ практических проектов и помощь в трудоустройстве в ведущих фирмах.

Изучите курс машинного обучения в лучших университетах мира. Заработайте программы Masters, Executive PGP или Advanced Certificate Programs, чтобы ускорить свою карьеру.

Что вы подразумеваете под линейной регрессией?

Линейная регрессия — это тип прогнозирующего численного анализа, с помощью которого мы можем найти значение неизвестной переменной с помощью зависимой переменной. Это также объясняет связь между одной зависимой и одной или несколькими независимыми переменными. Линейная регрессия — это статистический метод демонстрации связи между двумя переменными. Линейная регрессия строит линию тренда из набора точек данных. Линейную регрессию можно использовать для создания модели прогнозирования на основе, казалось бы, случайных данных, таких как диагнозы рака или цены на акции. Существует несколько методов расчета линейной регрессии. Обычный метод наименьших квадратов, который оценивает неизвестные переменные в данных и визуально преобразует их в сумму вертикальных расстояний между точками данных и линией тренда, является одним из наиболее распространенных.

Каковы недостатки линейной регрессии?

В большинстве случаев регрессионный анализ используется в исследованиях для установления наличия связи между переменными. Однако корреляция не подразумевает причинно-следственной связи, поскольку связь между двумя переменными не означает, что одна из них вызывает появление другой. Даже линия в базовой линейной регрессии, которая хорошо соответствует точкам данных, может не гарантировать взаимосвязь между обстоятельствами и логическими результатами. Используя модель линейной регрессии, вы можете определить, существует ли какая-либо корреляция между переменными. Дополнительные исследования и статистический анализ потребуются для определения точного характера связи и того, является ли одна переменная причиной другой.

Каковы основные предположения линейной регрессии?

В линейной регрессии есть три ключевых предположения. Зависимая и независимая переменные должны, прежде всего, иметь линейную связь. Диаграмма рассеяния зависимых и независимых переменных используется для проверки этой взаимосвязи. Во-вторых, мультиколлинеарность между независимыми переменными в наборе данных должна быть минимальной или нулевой. Это означает, что независимые переменные не связаны между собой. Значение должно быть ограничено, что определяется требованиями домена. Гомоскедастичность – третий фактор. Предположение о том, что ошибки распределены равномерно, является одним из наиболее существенных предположений.