Начало работы с отрицательной биномиальной регрессией: пошаговое руководство

Техника отрицательной биномиальной регрессии используется для моделирования счетных переменных. Метод почти аналогичен методу множественной регрессии. Однако есть разница в том, что в случае отрицательной биномиальной регрессии зависимая переменная, то есть Y, следует отрицательному биномиальному распределению. Поэтому значения переменной могут быть неотрицательными целыми числами, такими как 0, 1, 2.

Этот метод также является расширением регрессии Пуассона, которое делает послабление в предположении, что среднее значение равно дисперсии. Одна из традиционных моделей биномиальной регрессии, определяемая как «NB2», основана на смешанном распределении гаммы Пуассона.

Метод регрессии Пуассона обобщается добавлением переменной гамма-шума. Эта переменная имеет среднее значение, равное единице, а также параметр масштаба, равный «v».

Вот несколько примеров отрицательной биномиальной регрессии:

• Администрация школы провела исследование, чтобы изучить посещаемость старшеклассников из двух школ. Факторы, которые могут повлиять на посещаемость, могут включать дни, когда младшие школьники отсутствовали в школе. Кроме того, программа, в которой они были зачислены.
• Исследователь из исследования, связанного со здоровьем, провел исследование того, сколько пожилых людей посетили больницу за последние 12 месяцев. Исследование было основано на индивидуальных характеристиках и планах медицинского страхования, которые покупали пожилые люди.

Пример отрицательной биномиальной регрессии

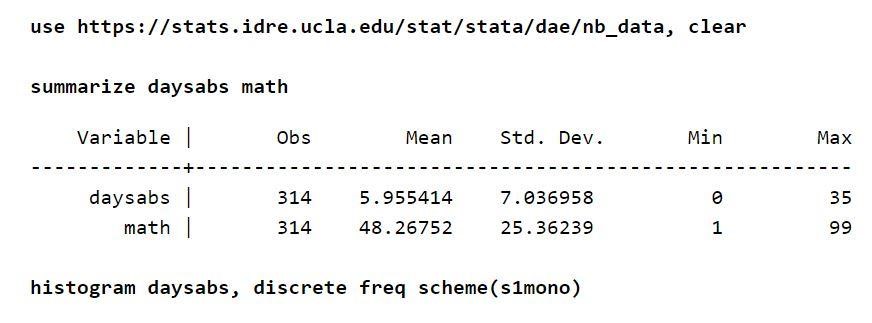
Предположим, что в списке посещаемости около 314 учеников средней школы. Данные взяты из двух городских школ и сохранены в файле с именем nb_data.dta. Интересная переменная отклика в этом примере — дни отсутствия, которые называются выходными днями. Присутствует одна переменная, «математика», которая определяет оценку по математике для каждого учащегося. Есть еще одна переменная, которая называется «prog». Эта переменная указывает программу, в которой зачислены студенты.

Источник

Каждая из переменных имеет около 314 наблюдений. Следовательно, распределения между переменными также разумны. Кроме того, учитывая переменную результата, безусловное среднее значение ниже дисперсии.

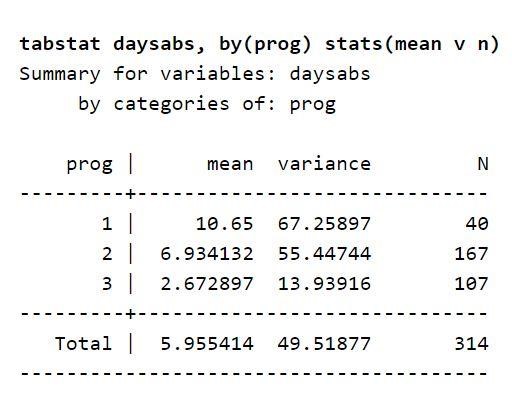
Теперь сосредоточьтесь на описании переменной, рассматриваемой в наборе данных. В таблице указано среднее количество дней, когда учащийся отсутствовал в школе по каждому типу программы. Это говорит о том, что программа переменного типа может предсказывать дни, когда учащийся отсутствовал в школе. Вы также можете использовать его для прогнозирования переменной результата. Это связано с тем, что среднее значение переменной результата зависит от переменной prog. Кроме того, значения дисперсии выше, чем на каждом уровне переменной prog. Эти значения называются дисперсиями и средними. Существующие различия предполагают наличие сверхдисперсии, в связи с чем целесообразным будет использование отрицательной биномиальной модели.

Источник

Исследователь может рассмотреть несколько методов анализа для этого типа исследования. Эти методы описаны ниже. Вот несколько методов анализа, которые пользователь может использовать для анализа регрессионной модели:

1. Отрицательная биномиальная регрессия

Метод отрицательной биномиальной регрессии следует использовать при наличии слишком разбросанных данных. Это означает, что значение условной дисперсии больше или превышает значение условного среднего. Метод считается обобщенным методом регрессии Пуассона. Это связано с тем, что оба метода имеют одинаковую структуру среднего. Но в отрицательной биномиальной регрессии есть дополнительный параметр, используемый для моделирования сверхдисперсии. Доверительные интервалы считаются более узкими, чем регрессия страсти, когда условное распределение чрезмерно разбросано по переменной результата.

2. Регрессия Пуассона

При моделировании данных подсчета используется метод регрессии Пуассона. Для моделирования переменных подсчета в регрессии Пуассона можно использовать множество расширений.

3. МНК-регрессия

Результаты подсчета переменных иногда логарифмически преобразовываются, а затем анализируются с помощью метода регрессии МНК. Однако иногда возникают проблемы, связанные с методом МНК-регрессии. Этими проблемами могут быть потеря данных из-за создания любого неопределенного значения путем рассмотрения журнала нулевого значения. Кроме того, он может быть сгенерирован из-за отсутствия моделирования рассредоточенных данных.

4. Модели с нулевым накачиванием

Эти типы моделей пытаются учесть все лишние нули в модели.

Анализ с использованием отрицательной биномиальной регрессии

Команда «nbreg» используется для оценки модели отрицательной биномиальной регрессии. Перед переменной «prog» стоит «i». Наличие «i» указывает на то, что переменная имеет тип factor, т. е. категориальная переменная. Они должны быть включены в модель в качестве индикаторных переменных.

• Вывод модели начинается с журнала итераций. Он начинается с подгонки модели Пуассона, за которой следует нулевая модель, а затем модель отрицательного бинома. Метод использует оценку максимального правдоподобия и продолжает повторяться до тех пор, пока не произойдет изменение значения окончательного журнала. Вероятность журнала используется для сравнения моделей.
• Следующая информация находится в заголовочном файле.
• Информация о коэффициентах отрицательной биномиальной регрессии находится чуть ниже заголовка. Коэффициенты генерируются для каждой переменной вместе с ошибками, такими как p-значения, z-показатели. Также существует доверительный интервал 95% для всех коэффициентов. Коэффициент для «математической» переменной равен -0,006, что означает, что она статистически значима. Результат означает, что при увеличении переменной «math» на одну единицу ожидаемое количество дней отсутствия уменьшается на значение 0,006. Кроме того, значение индикаторной переменной 2. prog представляет собой ожидаемую разницу в подсчете журнала между двумя группами (группа 2 и контрольная группа).
• Выполняется оценка параметра для логарифмического перераспределения, а затем отображается непреобразованное значение. В модели Пуассона значение равно нулю.
• Под таблицей коэффициентов находится информация о правдоподобии теста отношения. Модель можно дополнительно понять с помощью команд «поля».

Процесс выполнения отрицательного биномиального регрессионного анализа в Python

Необходимые пакеты для выполнения процесса регрессии необходимо импортировать из Python. Эти пакеты перечислены ниже:

• импортировать statsmodels.api как sm
• импортировать matplotlib.pyplot как plt
• импортировать numpy как np
• от patsy import dmatrics
• импортировать панд как pd

Соображения относительно отрицательной биномиальной регрессии

Есть несколько вещей, которые следует учитывать при применении метода анализа отрицательной биномиальной регрессии. Это включает:

• При наличии небольших выборок метод отрицательной биномиальной регрессии не рекомендуется.
• Иногда присутствуют лишние нули, которые могут быть причиной сверхдисперсии. Эти нули могут быть сгенерированы из-за процесса добавления генерации данных. В таких случаях рекомендуется использовать метод нулевой модели.
• Если в процессе формирования данных не учитываются нули, то в таких случаях рекомендуется использовать метод модели с усечением нулями.
• Существует переменная воздействия, связанная с данными подсчета. Переменная обозначает время, когда есть шанс, что событие может произойти. Эта переменная необходима для включения в модель отрицательной биномиальной регрессии. Это делается с помощью опции exp().
• Переменная результата не может быть отрицательным значением в модели анализа отрицательной биномиальной регрессии. Кроме того, переменная экспозиции не может иметь значение 0.
• Команду «glm» также можно использовать для запуска метода анализа отрицательной биномиальной регрессии. Это можно сделать через ссылку журнала, а также семейство биномов.
• Для получения остатков требуется команда «glm». Это делается для того, чтобы проверить, есть ли какие-либо другие предположения в модели отрицательной биномиальной регрессии.
• Существуют различные меры псевдо-R-квадрата. Однако каждая мера предоставляет информацию, аналогичную информации, предоставляемой R-квадратом в регрессии МНК.

Вывод

В статье обсуждалась тема отрицательной биномиальной регрессии . Мы видели, что он почти аналогичен методу множественных регрессий и представляет собой обобщенную форму распределения Пуассона. Существует несколько применений метода. Этот метод также можно применять с помощью языка программирования python или в R.

Также представлено несколько тематических исследований, которые показывают его применение в таких исследованиях, как старение. Кроме того, классическими моделями регрессии, которые можно использовать для данных подсчета, являются регрессия Пуассона, отрицательная биномиальная регрессия и геометрическая регрессия. Эти методы принадлежали к семейству линейных моделей и были включены почти во все статистические пакеты, такие как система R.

Если вы хотите преуспеть в машинном обучении и хотите изучить область данных, вы можете проверить курс Executive PG Program in Machine Learning & AI, предлагаемый upGrad. Итак, если вы работаете профессионалом, который мечтает стать экспертом в области машинного обучения, приходите и получите опыт обучения у экспертов. Более подробную информацию можно получить через наш веб-сайт. По любым вопросам наша команда может помочь вам быстро.

Повысьте свою карьеру в области машинного обучения и искусственного интеллекта

Подать заявку на получение исполнительной сертификации в Ai-ml от IIITB