Изучите наивный алгоритм Байеса для машинного обучения [с примерами]
Опубликовано: 2021-02-25Оглавление
Введение
В математике и программировании одни из самых простых решений обычно являются самыми мощными. Наивный алгоритм Байеса является классическим примером этого утверждения. Несмотря на сильное и быстрое продвижение и развитие в области машинного обучения, этот алгоритм наивного Байеса по-прежнему остается одним из наиболее широко используемых и эффективных алгоритмов. Наивный алгоритм Байеса находит применение в различных задачах, включая задачи классификации и задачи обработки естественного языка (NLP).
Математическая гипотеза теоремы Байеса служит фундаментальной концепцией этого наивного байесовского алгоритма. В этой статье мы рассмотрим основы теоремы Байеса, алгоритма наивного Байеса, а также его реализацию на Python с примером задачи в реальном времени. Наряду с этим мы также рассмотрим некоторые преимущества и недостатки наивного байесовского алгоритма по сравнению с его конкурентами.
Основы вероятности
Прежде чем мы приступим к пониманию теоремы Байеса и наивного байесовского алгоритма, давайте освежим наши знания об основах вероятности.
Как мы все знаем по определению, для данного события A вероятность его возникновения определяется как P(A). В теории вероятности два события А и В называются независимыми событиями, если наступление события А не влияет на вероятность наступления события В, и наоборот. С другой стороны, если одно событие изменяет вероятность другого, то они называются зависимыми событиями.
Давайте познакомимся с новым термином под названием условная вероятность . В математике условная вероятность для двух событий A и B, определяемая как P (A | B), определяется как вероятность возникновения события A при условии, что событие B уже произошло. В зависимости от отношения между двумя событиями A и B относительно того, являются ли они зависимыми или независимыми, условная вероятность рассчитывается двумя способами.
- Условная вероятность двух зависимых событий A и B определяется как P (A | B) = P (A и B) / P (B)
- Выражение для условной вероятности двух независимых событий A и B имеет вид: P (A | B) = P (A)
Зная математику вероятности и условной вероятности, давайте теперь перейдем к теореме Байеса.

Теорема Байеса
В статистике и теории вероятностей теорема Байеса, также известная как правило Байеса, используется для определения условной вероятности событий. Другими словами, теорема Байеса описывает вероятность события на основе предварительного знания условий, которые могут иметь отношение к событию.
Чтобы понять это проще, учтите, что нам нужно знать, что вероятность того, что цена дома очень высока. Если мы знаем о других параметрах, таких как наличие поблизости школ, медицинских магазинов и больниц, то мы можем сделать более точную оценку того же самого. Это именно то, что делает теорема Байеса.
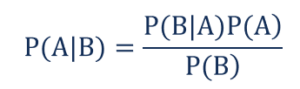
Такой,
- P(A|B) – условная вероятность возникновения события A при условии, что произошло событие B, также известное как апостериорная вероятность .
- P(B|A) – условная вероятность наступления события B при условии, что событие A произошло, также известная как вероятность правдоподобия .
- P(A) – вероятность наступления события A, также известная как априорная вероятность.
- P(B) – вероятность наступления события B, также известная как предельная вероятность.
Предположим, у нас есть простая задача машинного обучения с «n» независимыми переменными, а зависимая переменная, которая является выходом, является логическим значением (True или False). Предположим, что независимые атрибуты являются категориальными по своей природе, давайте рассмотрим 2 категории для этого примера. Следовательно, с этими данными нам нужно рассчитать значение вероятности правдоподобия, P (B | A).
Следовательно, наблюдая за вышеизложенным, мы обнаруживаем, что нам нужно рассчитать 2 * (2 ^ n -1 ) параметров, чтобы изучить эту модель машинного обучения. Точно так же, если у нас есть 30 булевых независимых атрибутов, то общее количество вычисляемых параметров будет близко к 3 миллиардам, что чрезвычайно дорого для вычислений.
Эта трудность построения модели машинного обучения с помощью теоремы Байеса привела к рождению и развитию наивного байесовского алгоритма.
Наивный байесовский алгоритм
Чтобы быть практичной, вышеупомянутая сложность теоремы Байеса должна быть уменьшена. Это точно достигается в наивном байесовском алгоритме за счет небольшого количества предположений. Сделанные предположения заключаются в том, что каждая функция вносит независимый и равный вклад в результат.
Наивный алгоритм Байеса — это алгоритм обучения с учителем, основанный на теореме Байеса, которая в основном используется при решении задач классификации. Это один из самых простых и точных классификаторов, которые строят модели машинного обучения для быстрого прогнозирования. Математически это вероятностный классификатор, поскольку он делает прогнозы, используя функцию вероятности событий.
Пример проблемы
Чтобы понять логику предположений, давайте рассмотрим простой набор данных, чтобы получить лучшее представление.
| Цвет | Тип | Источник | Кража? |
| Чернить | Седан | Импортировано | да |
| Чернить | внедорожник | Импортировано | Нет |
| Чернить | Седан | Одомашненный | да |
| Чернить | Седан | Импортировано | Нет |
| коричневый | внедорожник | Одомашненный | да |
| коричневый | внедорожник | Одомашненный | Нет |
| коричневый | Седан | Импортировано | Нет |
| коричневый | внедорожник | Импортировано | да |
| коричневый | Седан | Одомашненный | Нет |
Из приведенного выше набора данных мы можем вывести концепции двух предположений, которые мы определили для наивного байесовского алгоритма выше.
- Первое предположение состоит в том, что все признаки независимы друг от друга. Здесь мы видим, что каждый атрибут независим, например, красный цвет не зависит от типа и происхождения автомобиля.
- Далее, каждой функции следует придать равную важность. Точно так же знания только о типе и происхождении автомобиля недостаточны для прогнозирования результата задачи. Следовательно, ни одна из переменных не является нерелевантной, и, следовательно, все они вносят равный вклад в результат.
Подводя итог, можно сказать, что А и В условно независимы при заданном С тогда и только тогда, когда при знании того, что происходит С, знание о том, происходит ли А, не дает информации о вероятности наступления В, а знание о том, происходит ли В, не дает информации о вероятность возникновения А. Эти предположения делают алгоритм Байеса Наивным . Отсюда и название — наивный байесовский алгоритм.
Следовательно, для приведенной выше проблемы теорему Байеса можно переписать как –
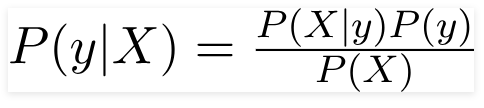
Такой,
- Независимый вектор признаков, X = (x 1 , x 2 , x 3 ……x n ), представляющий такие признаки, как цвет, тип и происхождение автомобиля.
- Выходная переменная y имеет только два результата Да или Нет.
Следовательно, подставляя приведенные выше значения, мы получаем наивную байесовскую формулу:
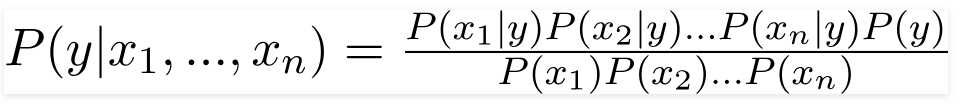
Чтобы рассчитать апостериорную вероятность P (y | X), мы должны создать таблицу частот для каждого атрибута по отношению к выходным данным. Затем преобразуем таблицы частот в таблицы правдоподобия, после чего мы, наконец, используем наивное байесовское уравнение для расчета апостериорной вероятности для каждого класса. В качестве результата прогноза выбирается класс с наибольшей апостериорной вероятностью. Ниже приведены таблицы частоты и вероятности для всех трех предикторов.
Таблица вероятностей цветов Таблица вероятностей цветов
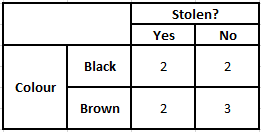
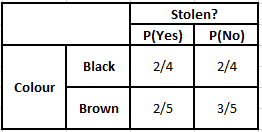
Таблица частот типов Таблица вероятностей типов
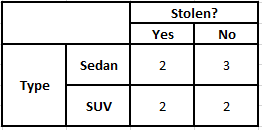
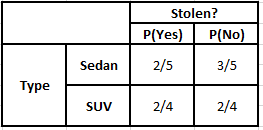

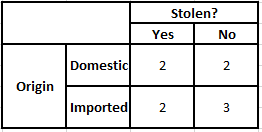
Таблица частот происхождения Таблица вероятностей происхождения
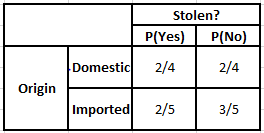
Рассмотрим случай, когда нам нужно рассчитать апостериорные вероятности для следующих условий:
| Цвет | Тип | Источник |
| коричневый | внедорожник | Импортировано |
Таким образом, из приведенной выше формулы мы можем рассчитать апостериорные вероятности, как показано ниже:
P(Да | X) = P(Коричневый | Да) * P(Внедорожник | Да) * P(Импортный | Да) * P(Да)
= 2/5 * 2/4 * 2/5 * 1
= 0,08
P(Нет | X) = P(Коричневый | Нет) * P(Внедорожник | Нет) * P(Импортный | Нет) * P(Нет)
= 3/5 * 2/4 * 3/5 * 1
= 0,18
Из вычисленных выше значений, поскольку апостериорные вероятности для «Нет» больше, чем «Да» (0,18>0,08), можно сделать вывод, что автомобиль коричневого цвета, тип внедорожника импортного происхождения классифицируется как «Нет». Следовательно, машина не украдена.
Реализация на Python
Теперь, когда мы поняли математику алгоритма наивного Байеса, а также визуализировали его на примере, давайте рассмотрим его код машинного обучения на языке Python.
Связанный: Наивный байесовский классификатор
Анализ проблемы
Чтобы реализовать программу наивной байесовской классификации в машинном обучении с использованием Python, мы будем использовать очень известный «набор данных Iris Flower». Набор данных о цветке ириса или набор данных об ирисе Фишера — это многомерный набор данных, представленный британским статистиком, евгеником и биологом Рональдом Фишером в 1998 году. Это очень небольшой и базовый набор данных, который состоит из очень менее числовых данных, содержащих информацию о 3 классах. цветов, принадлежащих к видам ирисов, которые:
- Ирис Сетоса
- Ирис разноцветный
- Ирис Вирджиния
Имеется 50 образцов каждого из трех видов , что составляет общий набор данных из 150 строк. 4 атрибута (или) независимых переменных, которые используются в этом наборе данных:
- длина чашелистика в см
- ширина чашелистика в см
- длина лепестка в см
- ширина лепестка в см
Зависимой переменной является « вид » цветка, который идентифицируется четырьмя указанными выше атрибутами.
Шаг 1 – Импорт библиотек
Как всегда, первым шагом в построении любой модели машинного обучения будет импорт соответствующих библиотек. Для этого мы загрузим библиотеки NumPy, Mathplotlib и Pandas для предварительной обработки данных.
импортировать numpy как np
импортировать matplotlib.pyplot как plt
импортировать панд как pd
Шаг 2 — Загрузка набора данных
Набор данных цветов ириса, который будет использоваться для обучения наивного байесовского классификатора, должен быть загружен в кадр данных Pandas. 4 независимые переменные должны быть присвоены переменной X, а переменная окончательного выходного вида назначена переменной y.
набор данных = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' ) X = набор данных.iloc[:,:4].values
y = набор данных ['вид'].valuesdataset.head(5)>>
sepal_length sepal_width лепесток_длина лепесток_ширина виды
5,1 3,5 1,4 0,2 щетинковидная
4,9 3,0 1,4 0,2 щетина
4,7 3,2 1,3 0,2 щетинковидная
4,6 3,1 1,5 0,2 щетинковидная
5,0 3,6 1,4 0,2 щетина
Шаг 3 — Разделение набора данных на обучающий набор и тестовый набор
После загрузки набора данных и переменных следующим шагом будет подготовка переменных, которые будут проходить процесс обучения. На этом этапе мы должны разделить переменные X и y на обучающие и тестовые наборы данных. Для этого мы случайным образом назначим 80% данных обучающему набору, который будет использоваться в целях обучения, а оставшиеся 20% данных — тестовому набору, на котором обученный наивный байесовский классификатор будет проверяться на точность.
из sklearn.model_selection импорта train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0,2)
Шаг 4 – Масштабирование функций
Хотя это дополнительный процесс для этого небольшого набора данных, я добавляю его, чтобы вы могли использовать его в большом наборе данных. При этом данные в обучающем и тестовом наборах масштабируются до диапазона значений от 0 до 1. Это снижает вычислительные затраты.
из sklearn.preprocessing импортировать StandardScaler
sc = Стандартный масштаб()
X_train = sc.fit_transform (X_train)
X_test = sc.transform(X_test)
Шаг 5 — Обучение модели наивной байесовской классификации на обучающем наборе
Именно на этом этапе мы импортируем класс Naive Bayes из библиотеки sklearn. Для этой модели мы используем модель Гаусса, есть несколько других моделей, таких как Бернулли, Категориальная и Полиномиальная. Таким образом, X_train и y_train подгоняются к переменной классификатора в целях обучения.
из sklearn.naive_bayes импортировать GaussianNB
классификатор = GaussianNB()
classifier.fit(X_train, y_train)
Шаг 6 — Прогнозирование результатов тестового набора —
Мы прогнозируем класс видов для тестового набора, используя обученную модель, и сравниваем его с реальными значениями класса видов.
y_pred = классификатор.predict(X_test)
df = pd.DataFrame({'Реальные значения': y_test, 'Прогнозируемые значения': y_pred})
дф>>
Реальные значения Прогнозируемые значения
сетоза сетоза
сетоза сетоза
виргиния
лишай
сетоза сетоза
сетоза сетоза
… … … … …
виргинский лишай
виргиния
сетоза сетоза
сетоза сетоза
лишай
лишай
В приведенном выше сравнении мы видим, что есть одно неверное предсказание, которое предсказало Versicolor вместо virginica.
Шаг 7 – Матрица путаницы и точность
Поскольку мы имеем дело с классификацией, лучший способ оценить нашу модель классификатора — распечатать матрицу путаницы вместе с ее точностью на тестовом наборе.
из sklearn.metrics импортировать путаницу_матрицу
cm = растерянность_матрица (y_test, y_pred) из импорта sklearn.metrics, точность_показателя

печать («Точность:», точность_оценка (y_test, y_pred))
см>>Точность: 0,9666666666666667
>>массив([[14, 0, 0],
[0, 7, 0],
[0, 1, 8]])
Заключение
Таким образом, в этой статье мы рассмотрели основы наивного байесовского алгоритма, поняли математику, стоящую за классификацией, а также пример, решенный вручную. Наконец, мы внедрили код машинного обучения для решения популярного набора данных с использованием алгоритма наивной байесовской классификации.
Если вам интересно узнать больше об искусственном интеллекте и машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, Статус выпускника IIIT-B, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.
Как вероятность полезна в машинном обучении?
Возможно, нам придется принимать решения на основе частичной или неполной информации в реальных сценариях. Вероятность помогает нам количественно оценить неопределенность в таких системах и управлять риском задачи. Традиционный метод работает только для детерминированных результатов конкретных действий, но в любой модели прогнозирования всегда присутствует некоторая степень неопределенности. Эта неопределенность может исходить из многих параметров входных данных, таких как шум в данных. Кроме того, байесовские взгляды из теорем вероятности могут помочь в распознавании образов из входных данных. Для этого вероятность использует концепцию оценки максимального правдоподобия и, следовательно, помогает получить соответствующие результаты.
В чем польза матрицы путаницы?
Матрица путаницы представляет собой матрицу 2x2, используемую для интерпретации эффективности модели классификации. Чтобы это работало, должны быть известны истинные значения входных данных, поэтому они не могут быть представлены для немаркированных данных. Он состоит из количества ложноположительных результатов (FP), истинно положительных результатов (TP), ложноотрицательных результатов (FN) и истинно отрицательных результатов (TN). Прогнозы классифицируются по этим классам с использованием подсчета из обучающего набора и тестового набора. Это помогает нам визуализировать полезные параметры, такие как точность, воспроизводимость и специфичность. Он относительно прост для понимания и дает четкое представление об алгоритме.
Какие существуют типы наивной байесовской модели?
Все типы в первую очередь основаны на теореме Байеса. Наивная байесовская модель обычно имеет три типа: гауссовскую, бернуллиевскую и полиномиальную. Гауссовский наивный байесовский метод помогает с непрерывными значениями входных параметров и предполагает, что все классы входных данных распределены равномерно. Наивный байесовский метод Бернулли — это модель, основанная на событиях, в которой признаки данных независимы и представлены логическими значениями. Полиномиальный наивный байесовский алгоритм также основан на событийной модели. Он имеет функции данных в векторной форме, которая представляет соответствующие частоты в зависимости от возникновения событий.
