7 наиболее часто используемых алгоритмов машинного обучения в Python, о которых вы должны знать

Машинное обучение — это ветвь искусственного интеллекта (ИИ), которая занимается компьютерными алгоритмами, используемыми для любых данных. Он фокусируется на автоматическом обучении на основе поступающих в него данных и дает нам результаты, каждый раз улучшая предыдущие прогнозы.

Лучшие алгоритмы машинного обучения, используемые в Python

Ниже приведены некоторые из лучших алгоритмов машинного обучения, используемых в Python, а также фрагменты кода, демонстрирующие их реализацию и визуализацию границ классификации.

1. Линейная регрессия

Линейная регрессия — один из наиболее часто используемых методов машинного обучения с учителем. Как следует из названия, эта регрессия пытается смоделировать взаимосвязь между двумя переменными, используя линейное уравнение и подгоняя эту линию к наблюдаемым данным. Этот метод используется для оценки реальных непрерывных значений, таких как общий объем продаж или стоимость домов.

Линия наилучшего соответствия также называется линией регрессии. Он определяется следующим уравнением:

Y = а * Х + б

где Y — зависимая переменная, a — наклон, X — независимая переменная, а b — значение точки пересечения. Коэффициенты a и b получаются путем минимизации квадрата разницы этого расстояния между различными точками данных и уравнением линии регрессии.

# синтетический набор данных для простой регрессии

из sklearn.datasets импортировать make_regression

plt.figure()

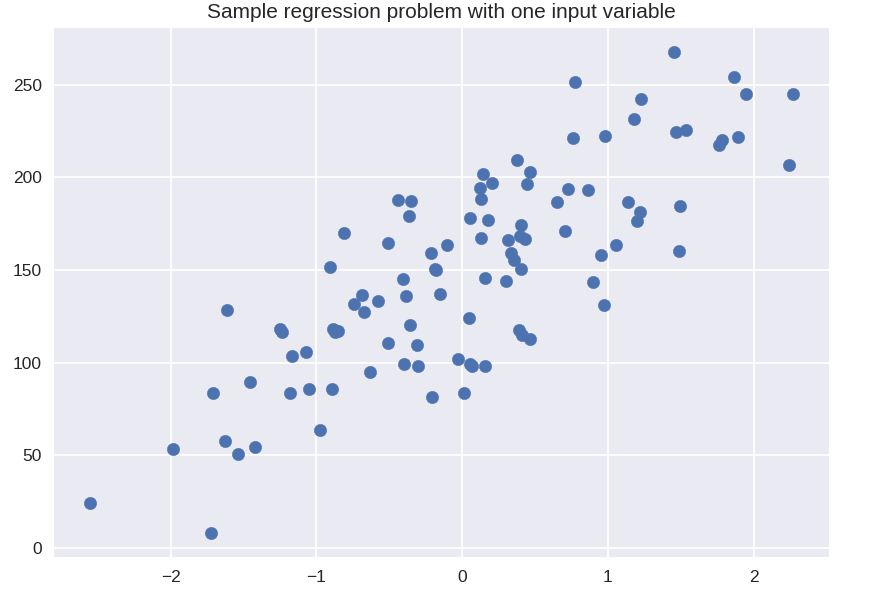
plt.title('Пример задачи регрессии с одной входной переменной')

X_R1, y_R1 = make_regression (n_samples = 100, n_features = 1, n_informative = 1, смещение = 150,0, шум = 30, random_state = 0)

plt.scatter(X_R1, y_R1, маркер = 'o', s = 50)

plt.show()

из sklearn.linear_model импортировать линейную регрессию

X_train, X_test, y_train, y_test = train_test_split( X_R1, y_R1,

случайное_состояние = 0 )

linreg = LinearRegression().fit( X_train, y_train )

print('коэффициент линейной модели (w): {}'.format(linreg.coef_))

print('перехват линейной модели (b): {:.3f}'z.format(linreg.intercept_))

print('Оценка R-квадрата (обучение): {:.3f}'.format(linreg.score(X_train, y_train))

print('Оценка R-квадрата (тест): {:.3f}'.format(linreg.score(X_test, y_test)) )

Выход

коэффициент линейной модели (w): [ 45,71]

пересечение линейной модели (b): 148,446

Оценка R-квадрата (обучение): 0,679

Оценка R-квадрата (тест): 0,492

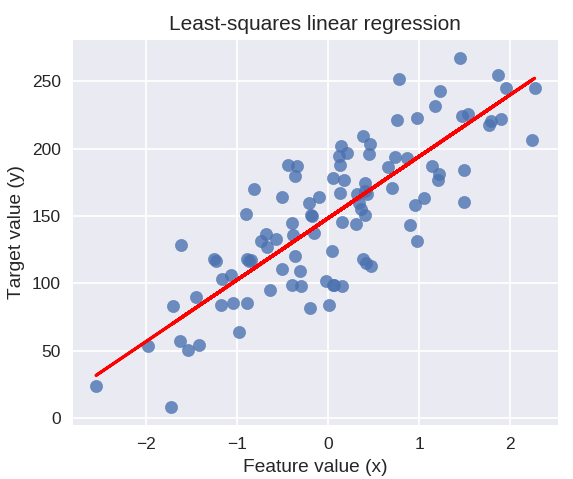
Следующий код нарисует подобранную линию регрессии на графике наших точек данных.

plt.figure( figsize = ( 5, 4 ))

plt.scatter( X_R1, y_R1, маркер = 'o', s = 50, альфа = 0,8)

plt.plot( X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-' )

plt.title('Линейная регрессия методом наименьших квадратов')

plt.xlabel('Значение функции (x)')

plt.ylabel('Целевое значение (y)')

plt.show()

Подготовка общего набора данных для изучения методов классификации

Следующие данные будут использоваться для демонстрации различных алгоритмов классификации, которые чаще всего используются в машинном обучении в Python.

Набор грибных данных UCI хранится в файле грибов.csv.

блокнот %matplotlib

импортировать панд как pd

импортировать numpy как np

импортировать matplotlib.pyplot как plt

из sklearn.decomposition импортировать PCA

из sklearn.model_selection импорта train_test_split

df = pd.read_csv('только чтение/грибы.csv')

df2 = pd.get_dummies( df )

df3 = df2.sample(фракция = 0,08)

X = df3.iloc[:, 2:]

у = df3.iloc[:, 1]

pca = PCA( n_components = 2 ).fit_transform( X )

X_train, X_test, y_train, y_test = train_test_split(pca, y, random_state = 0)

plt.figure (dpi = 120)

plt.scatter( pca[y.values ​​== 0, 0], pca[y.values ​​== 0, 1], alpha = 0,5, label = 'Съедобный', s = 2 )

plt.scatter( pca[y.values ​​== 1, 0], pca[y.values ​​== 1, 1], alpha = 0,5, label = 'Ядовитый', s = 2)

plt.legend()

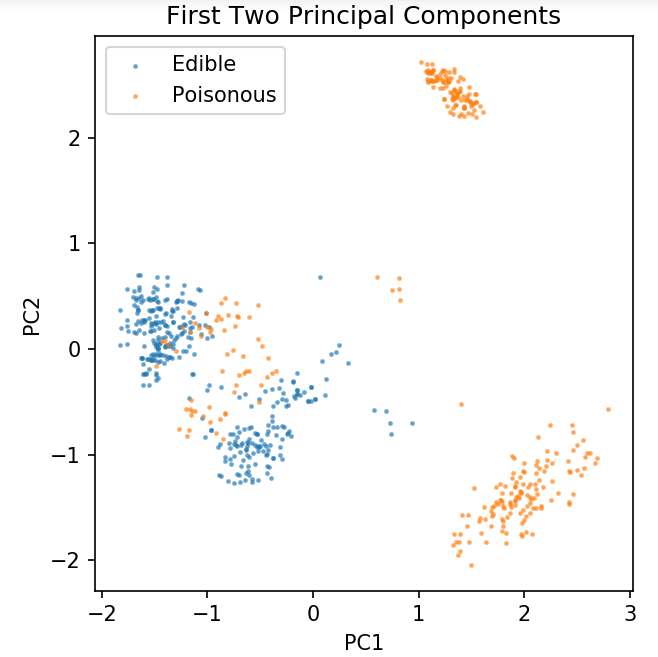
plt.title('Грибной набор данных\nПервые два основных компонента')

plt.xlabel('PC1')

plt.ylabel('PC2')

plt.gca().set_aspect('равно')

Мы будем использовать функцию, определенную ниже, чтобы получить границы решений различных классификаторов, которые мы будем использовать в наборе данных грибов.

def plot_mushroom_boundary( X, y, fit_model ):

plt.figure( figsize = (9.8, 5), dpi = 100)

для i, plot_type в enumerate(['Граница решения', 'Вероятность решения']):

plt.subplot( 1, 2, я + 1 )

mesh_step_size = 0.01 # размер шага в сетке

x_min, x_max = X[:, 0].min() – .1, X[:, 0].max() + .1

y_min, y_max = X[:, 1].min() – .1, X[:, 1].max() + .1

xx, yy = np.meshgrid( np.arange(x_min, x_max, mesh_step_size), np.arange(y_min, y_max, mesh_step_size))

если я == 0:

Z = fit_model.predict(np.c_[xx.ravel(), yy.ravel()])

еще:

пытаться:

Z = приспособленная_модель.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]

Кроме:

plt.text(0.4, 0.5, 'Вероятности недоступны', horizontalalignment = 'center', verticalalignment = 'center', transform = plt.gca().transAxes, fontsize = 12)

плт.ось('выкл')

перерыв

Z = Z.изменить форму( xx.форма )

plt.scatter( X[y.values ​​== 0, 0], X[y.values ​​== 0, 1], alpha = 0,4, label = 'Съедобный', s = 5)

plt.scatter( X[y.values ​​== 1, 0], X[y.values ​​== 1, 1], alpha = 0,4, label = 'Posionous', s = 5)

plt.imshow(Z, интерполяция = 'ближайший', cmap = 'RdYlBu_r', альфа = 0,15, степень = (x_min, x_max, y_min, y_max), происхождение = 'ниже')

plt.title(plot_type + '\n' + str(fitt_model).split('(')[0] + 'Точность теста:' + str(np.round(fitt_model.score(X, y), 5)) )

plt.gca().set_aspect('равно');

plt.tight_layout()

plt.subplots_adjust (сверху = 0,9, снизу = 0,08, wspace = 0,02)

2. Логистическая регрессия

В отличие от линейной регрессии, логистическая регрессия имеет дело с оценкой дискретных значений (двоичные значения 0/1, истина/ложь, да/нет). Этот метод также называется логит-регрессией. Это связано с тем, что он предсказывает вероятность события, используя логит-функцию для обучения заданных данных. Его значение всегда находится между 0 и 1 (поскольку вычисляется вероятность).

Логарифм шансов результатов строится как линейная комбинация переменной-предиктора следующим образом:

шансы = p / (1 – p) = вероятность наступления события или вероятность того, что событие не произойдет

ln(шансы) = ln(p/(1 – p))

logit( p ) = ln( p / (1 – p)) = b0 + b1X1 + b2X2 + b3X3 + … + bkXk

где р — вероятность наличия признака.

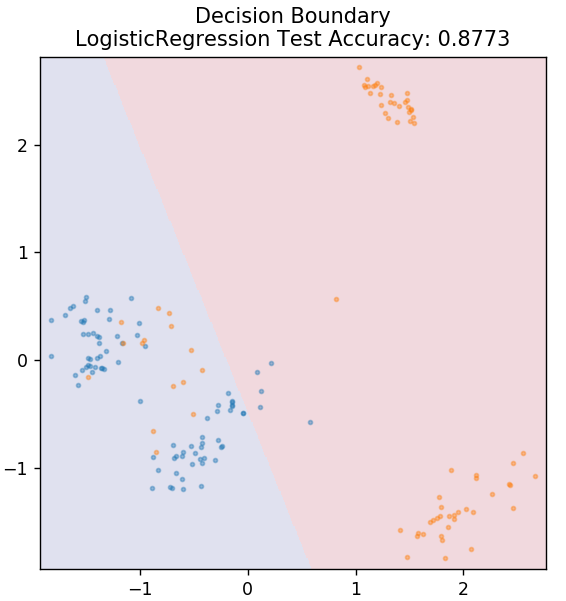
из sklearn.linear_model импортировать LogisticRegression

модель = Логистическая регрессия ()

model.fit(X_train, y_train)

plot_mushroom_boundary (X_test, y_test, модель)

Получите онлайн- сертификат искусственного интеллекта в ведущих университетах мира — магистерские программы, программы последипломного образования для руководителей и продвинутую программу сертификации в области машинного обучения и искусственного интеллекта, чтобы ускорить свою карьеру.

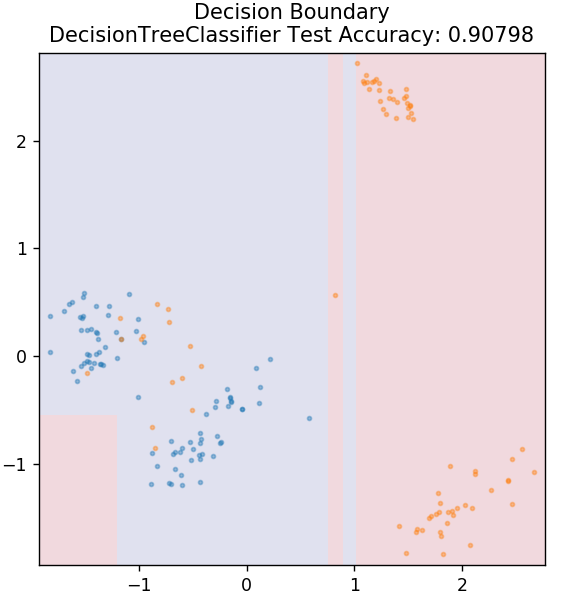
3. Дерево решений

Это очень популярный алгоритм, который можно использовать для классификации как непрерывных, так и дискретных переменных данных. На каждом этапе данные разбиваются на несколько однородных наборов на основе некоторых атрибутов/условий разделения.

из sklearn.tree импортировать DecisionTreeClassifier

модель = DecisionTreeClassifier (max_depth = 3)

model.fit(X_train, y_train)

plot_mushroom_boundary (X_test, y_test, модель)

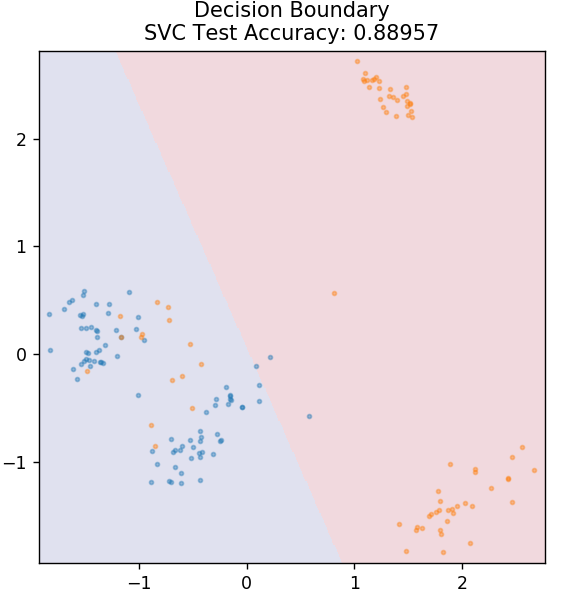
4. СВМ

SVM — это сокращение от «Машины опорных векторов». Здесь основная идея заключается в классификации точек данных с использованием гиперплоскостей для разделения. Цель состоит в том, чтобы найти такую ​​гиперплоскость, которая имеет максимальное расстояние (или запас) между точками данных как классов, так и категорий.

Мы выбираем плоскость таким образом, чтобы в будущем с максимальной достоверностью позаботиться о классификации неизвестных точек. SVM широко используются, потому что они обеспечивают высокую точность при очень низкой вычислительной мощности. SVM также можно использовать для решения проблем регрессии.

из sklearn.svm импортировать SVC

модель = SVC (ядро = 'линейный')

model.fit(X_train, y_train)

plot_mushroom_boundary (X_test, y_test, модель)

Оформить заказ: проекты Python на GitHub

5. Наивный Байес

Как следует из названия, алгоритм наивного Байеса — это алгоритм обучения с учителем, основанный на теореме Байеса . Теорема Байеса использует условные вероятности, чтобы дать вам вероятность события на основе некоторых заданных знаний.

Где,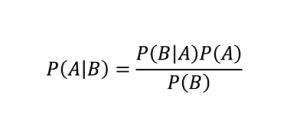

P (A | B): условная вероятность того, что событие A произойдет при условии, что событие B уже произошло. (Также называется апостериорной вероятностью)

P(A): Вероятность события A.

P(B): Вероятность события B.

P (B | A): условная вероятность того, что событие B произойдет при условии, что событие A уже произошло.

Вы спросите, почему этот алгоритм называется Наивным? Это связано с тем, что предполагается, что все вхождения событий независимы друг от друга. Таким образом, каждая функция отдельно определяет класс, к которому принадлежит точка данных, не имея никаких зависимостей между собой. Наивный Байес — лучший выбор для категоризации текста. Он будет достаточно хорошо работать даже с небольшими объемами обучающих данных.

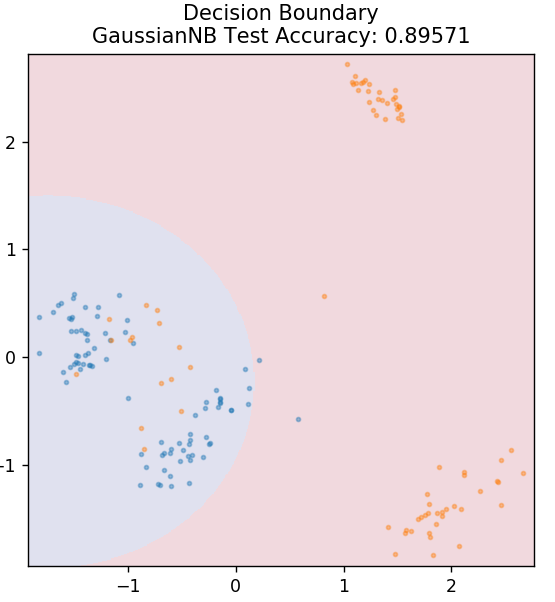
из sklearn.naive_bayes импортировать GaussianNB

модель = GaussianNB()

model.fit(X_train, y_train)

plot_mushroom_boundary (X_test, y_test, модель)

5. КНН

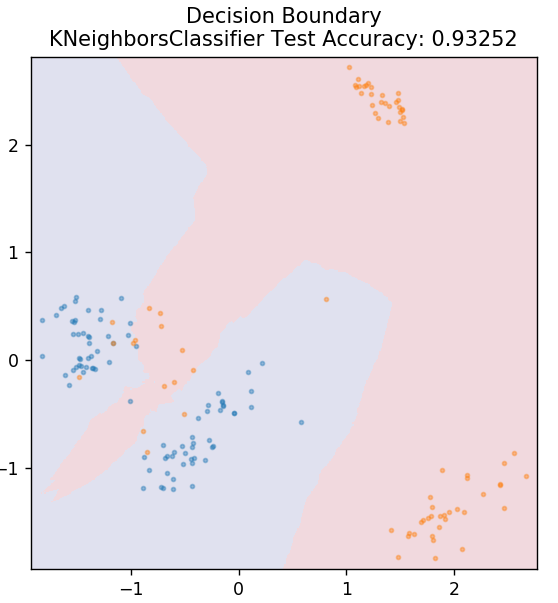
KNN расшифровывается как K-ближайшие соседи. Это очень широко используемый алгоритм обучения с учителем, который классифицирует тестовые данные в соответствии с их сходством с ранее классифицированными данными обучения. KNN не классифицирует все точки данных во время обучения. Вместо этого он просто сохраняет набор данных, а когда получает какие-либо новые данные, классифицирует эти точки данных на основе их сходства. Это делается путем вычисления евклидова расстояния K ближайших соседей (здесь n_neighbors ) этой точки данных.

из sklearn.neighbors импортировать KNeighborsClassifier

модель = KNeighborsClassifier (n_neighbors = 20)

model.fit(X_train, y_train)

plot_mushroom_boundary (X_test, y_test, модель)

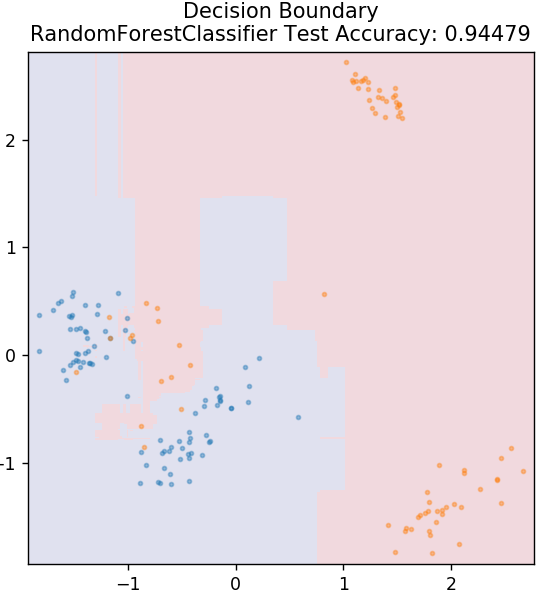
6. Случайный лес

Случайный лес — это очень простой и разнообразный алгоритм машинного обучения, использующий технику обучения с учителем. Как вы можете догадаться из названия, случайный лес состоит из большого количества деревьев решений, действующих как ансамбль. Каждое дерево решений определит выходной класс точек данных, и в качестве окончательного вывода модели будет выбран класс большинства. Идея заключается в том, что большее количество деревьев, работающих с одними и теми же данными, будет иметь более точные результаты, чем отдельные деревья.

из sklearn.ensemble импортировать RandomForestClassifier

модель = RandomForestClassifier()

model.fit(X_train, y_train)

plot_mushroom_boundary (X_test, y_test, модель)

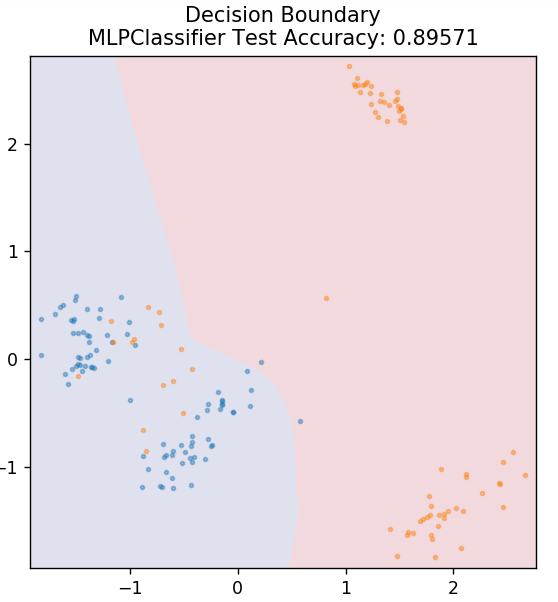
7. Многослойный персептрон

Многослойный персептрон (или MLP) — очень увлекательный алгоритм, относящийся к области глубокого обучения. В частности, он принадлежит к классу искусственных нейронных сетей с прямой связью (ИНС). MLP формирует сеть из нескольких персептронов, по крайней мере, с тремя слоями: входным слоем, выходным слоем и скрытым слоем (слоями). MLP способны различать данные, которые нелинейно разделимы.

Каждый нейрон в скрытых слоях использует функцию активации для перехода к следующему слою. Здесь алгоритм обратного распространения используется для фактической настройки параметров и, следовательно, для обучения нейронной сети. В основном его можно использовать для простых задач регрессии.

из sklearn.neural_network импортировать MLPClassifier

модель = MLPClassifier()

model.fit(X_train, y_train)

plot_mushroom_boundary (X_test, y_test, модель)

Читайте также: Идеи и темы проекта Python

Заключение

Мы можем сделать вывод, что разные алгоритмы машинного обучения дают разные границы решений и, следовательно, разная точность приводит к классификации одного и того же набора данных.

Невозможно объявить какой-либо алгоритм лучшим алгоритмом для всех типов данных в целом. Машинное обучение требует тщательных проб и ошибок для различных алгоритмов, чтобы определить, что лучше всего работает для каждого набора данных в отдельности. Список алгоритмов машинного обучения на этом явно не заканчивается. Существует огромное количество других методов, которые ждут своего изучения в библиотеке Python Scikit-Learn. Идите вперед и тренируйте свои наборы данных, используя все это, и получайте удовольствие!

Если вам интересно узнать больше о деревьях решений и машинном обучении, ознакомьтесь с программой Executive PG IIIT-B и upGrad по машинному обучению и искусственному интеллекту , которая предназначена для работающих профессионалов и предлагает более 450 часов интенсивного обучения, более 30 тематических исследований и задания, статус выпускника IIIT-B, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.