25 вопросов и ответов на собеседовании по машинному обучению — линейная регрессия
Опубликовано: 2022-09-08Общепринятой практикой является тестирование претендентов на науку о данных на часто используемых алгоритмах машинного обучения на собеседованиях. Эти обычные алгоритмы представляют собой линейную регрессию, логистическую регрессию, кластеризацию, деревья решений и т. д. Ожидается, что ученые, работающие с данными, будут обладать глубокими знаниями этих алгоритмов.
Мы проконсультировались с менеджерами по найму и специалистами по данным из различных организаций, чтобы узнать о типичных вопросах ML, которые они задают на собеседовании. На основе их обширных отзывов был подготовлен набор вопросов и ответов, чтобы помочь начинающим специалистам по данным в их беседах. Вопросы для интервью по линейной регрессии являются наиболее распространенными в интервью по машинному обучению. Вопросы и ответы по этим алгоритмам будут представлены в серии из четырех сообщений в блоге.
Лучшие онлайн-курсы по машинному обучению и курсы по искусственному интеллекту
| Магистр наук в области машинного обучения и искусственного интеллекта от LJMU | Высшая программа высшего образования в области машинного обучения и искусственного интеллекта от IIITB | |
| Продвинутая сертификационная программа по машинному обучению и НЛП от IIITB | Расширенная программа сертификации в области машинного обучения и глубокого обучения от IIITB | Программа Executive Post Graduate Program в области науки о данных и машинного обучения Университета Мэриленда |
| Чтобы изучить все наши курсы, посетите нашу страницу ниже. | ||
| Курсы по машинному обучению | ||
Каждое сообщение в блоге будет посвящено следующей теме: -
- Линейная регрессия
- Логистическая регрессия
- Кластеризация
- Деревья решений и вопросы, относящиеся ко всем алгоритмам
Давайте начнем с линейной регрессии!
1. Что такое линейная регрессия?
Проще говоря, линейная регрессия — это метод нахождения наилучшей прямой линии, соответствующей заданным данным, т. е. нахождения наилучшей линейной зависимости между независимыми и зависимыми переменными.
С технической точки зрения, линейная регрессия — это алгоритм машинного обучения, который находит наилучшую линейную зависимость для любых заданных данных между независимыми и зависимыми переменными. В основном это делается методом суммы квадратов остатков.
Востребованные навыки машинного обучения
| Курсы искусственного интеллекта | Курсы Табло |
| Курсы НЛП | Курсы глубокого обучения |

2. Сформулируйте предположения в модели линейной регрессии.
В модели линейной регрессии есть три основных предположения:
- Предположение о форме модели:
Предполагается, что существует линейная зависимость между зависимой и независимой переменными. Это известно как «предположение о линейности». - Предположения об остатках:
- Предположение о нормальности: предполагается, что члены ошибки ε (i) нормально распределены.
- Допущение о нулевом среднем: предполагается, что остатки имеют нулевое среднее значение.
- Предположение о постоянной дисперсии: Предполагается, что остаточные члены имеют одинаковую (но неизвестную) дисперсию, σ 2. Это предположение также известно как предположение об однородности или гомоскедастичности.
- Допущение о независимой ошибке: предполагается, что остаточные члены не зависят друг от друга, т. е. их парная ковариация равна нулю.
- Предположения об оценщиках:
- Независимые переменные измеряются без ошибок.
- Независимые переменные линейно независимы друг от друга, т.е. в данных нет мультиколлинеарности.
Объяснение:
- Это говорит само за себя.
- Если остатки не распределены нормально, их случайность теряется, что означает, что модель не может объяснить связь в данных.
Кроме того, среднее значение остатков должно быть равно нулю.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Это предполагаемая линейная модель, где ε — остаточный член.
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 х (i) + ε (i) )
Если ожидание (среднее) остатков E(ε (i) ) равно нулю, ожидания целевой переменной и модели становятся одинаковыми, что является одной из целей модели.
Остатки (также известные как члены ошибки) должны быть независимыми. Это означает отсутствие корреляции между остатками и прогнозируемыми значениями или между самими остатками. Если присутствует какая-то корреляция, это означает, что существует какая-то связь, которую регрессионная модель не может идентифицировать. - Если независимые переменные не являются линейно независимыми друг от друга, уникальность решения методом наименьших квадратов (или решения нормального уравнения) теряется.
Присоединяйтесь к онлайн-курсу по искусственному интеллекту в ведущих университетах мира — магистерским программам, программам последипломного образования для руководителей и продвинутой сертификационной программе в области машинного обучения и искусственного интеллекта, чтобы ускорить свою карьеру.
3. Что такое разработка признаков? Как вы применяете это в процессе моделирования?
Разработка функций — это процесс преобразования необработанных данных в функции, которые лучше представляют основную проблему для прогностических моделей.
, что приводит к повышению точности модели на невидимых данных.
С точки зрения непрофессионала, проектирование признаков означает разработку новых свойств, которые могут помочь вам лучше понять и смоделировать проблему. Разработка признаков бывает двух видов — управляемая бизнесом и управляемая данными. Разработка функций, ориентированная на бизнес, вращается вокруг включения функций с точки зрения бизнеса. Задача здесь состоит в том, чтобы преобразовать бизнес-переменные в характеристики проблемы. В случае разработки признаков, управляемых данными, добавляемые вами признаки не имеют существенной физической интерпретации, но они помогают модели прогнозировать целевую переменную.
К вашему сведению: бесплатный курс НЛП!
Чтобы применить разработку признаков, нужно полностью ознакомиться с набором данных. Это включает в себя знание того, что представляют собой данные, что они означают, каковы необработанные функции и т. д. Вы также должны иметь кристально ясное представление о проблеме, например, какие факторы влияют на целевую переменную, какова физическая интерпретация переменной. , так далее.
4. Какая польза от регуляризации? Объясните регуляризации L1 и L2.
Регуляризация — это метод, который используется для решения проблемы переобучения модели. Когда очень сложная модель реализуется на обучающих данных, она переобучается. Иногда простая модель может быть не в состоянии обобщить данные, а сложная модель переобучает. Для решения этой проблемы используется регуляризация.
Регуляризация — это не что иное, как добавление членов коэффициента (бета) к функции стоимости, так что члены наказываются и становятся малыми по величине. По сути, это помогает фиксировать тенденции в данных и в то же время предотвращает переоснащение, не позволяя модели стать слишком сложной.
- Регуляризация L1 или LASSO: здесь абсолютные значения коэффициентов добавляются к функции стоимости. Это можно увидеть в следующем уравнении; выделенная часть соответствует регуляризации L1 или LASSO. Этот метод регуляризации дает разреженные результаты, что также приводит к выбору признаков.
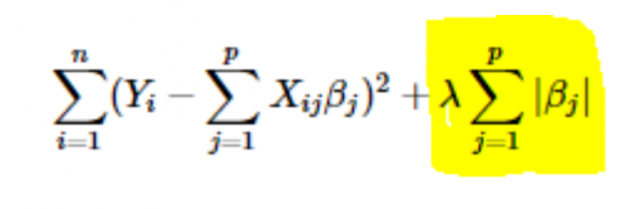
- Регуляризация L2 или Риджа: здесь квадраты коэффициентов добавляются к функции стоимости. Это можно увидеть в следующем уравнении, где выделенная часть соответствует регуляризации L2 или Риджа.
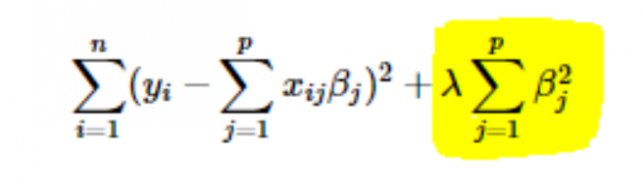
5. Как выбрать значение параметра скорости обучения (α)?
Выбор значения скорости обучения — непростое дело. Если значение слишком мало, алгоритму градиентного спуска требуется время, чтобы сходиться к оптимальному решению. С другой стороны, если значение скорости обучения велико, градиентный спуск превысит оптимальное решение и, скорее всего, никогда не сойдется к оптимальному решению.
Чтобы преодолеть эту проблему, вы можете попробовать разные значения альфы в диапазоне значений и построить график зависимости стоимости от количества итераций. Затем на основе графиков можно выбрать значение, соответствующее графику, показывающему быстрое уменьшение. 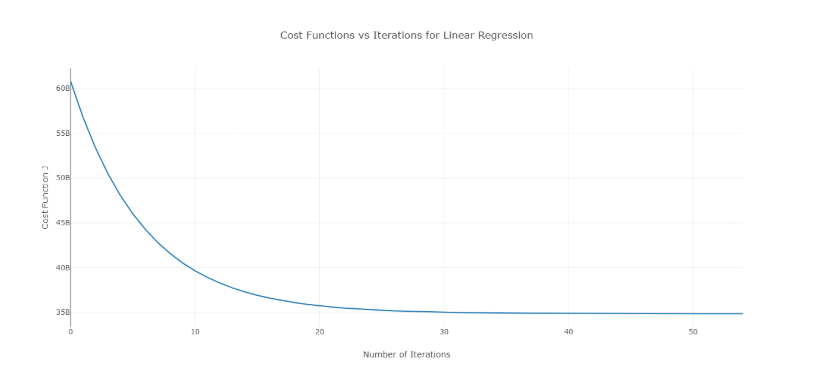
Вышеупомянутый график представляет собой идеальную кривую зависимости стоимости от количества итераций. Обратите внимание, что стоимость сначала уменьшается по мере увеличения количества итераций, но после определенных итераций градиентный спуск сходится, и стоимость больше не уменьшается.
Если вы видите, что стоимость увеличивается с количеством итераций, ваш параметр скорости обучения высок, и его необходимо уменьшить.
6. Как выбрать значение параметра регуляризации (λ)?
Выбор параметра регуляризации — непростое дело. Если значение λ слишком велико, это приведет к чрезвычайно малым значениям коэффициента регрессии β , что приведет к недообучению модели (высокое смещение — низкая дисперсия). С другой стороны, если значение λ равно 0 (очень маленькое), модель будет иметь тенденцию к переобучению обучающих данных (низкое смещение — высокая дисперсия).
Нет правильного способа выбрать значение λ . Что вы можете сделать, так это получить подвыборку данных и запустить алгоритм несколько раз на разных наборах. Здесь человек должен решить, насколько допустима дисперсия. Как только пользователь будет удовлетворен дисперсией, это значение λ может быть выбрано для полного набора данных.
Следует отметить, что выбранное здесь значение λ было оптимальным для этого подмножества, а не для всех обучающих данных.
7. Можем ли мы использовать линейную регрессию для анализа временных рядов?
Можно использовать линейную регрессию для анализа временных рядов, но результаты не многообещающие. Так что делать это, как правило, не рекомендуется. Причины этого —
- Данные временных рядов в основном используются для предсказания будущего, но линейная регрессия редко дает хорошие результаты для предсказания будущего, поскольку она не предназначена для экстраполяции.
- В основном данные временных рядов имеют закономерность, например, в часы пик, праздничные сезоны и т. д., которые, скорее всего, будут рассматриваться как выбросы в анализе линейной регрессии.
8. К какому значению близка сумма остатков линейной регрессии? Оправдывать.
Ответ Сумма остатков линейной регрессии равна 0. Линейная регрессия работает в предположении, что ошибки (остатки) нормально распределены со средним значением 0, т.е.
Y = β Т X + ε
Здесь Y — целевая или зависимая переменная,
β — вектор коэффициента регрессии,
X — матрица признаков, содержащая все признаки в виде столбцов,
ε — остаточный член такой, что ε ~ N( 0 ,σ2 ).
Таким образом, сумма всех остатков представляет собой ожидаемое значение остатков, умноженное на общее количество точек данных. Поскольку математическое ожидание остатков равно 0, сумма всех остаточных членов равна нулю.
Примечание : N(μ, σ2 ) — это стандартное обозначение нормального распределения, имеющего среднее значение μ и стандартное отклонение σ2 .
9. Как мультиколлинеарность влияет на линейную регрессию?
Ответ Мультиколлинеарность возникает, когда некоторые независимые переменные сильно коррелируют (положительно или отрицательно) друг с другом. Эта мультиколлинеарность вызывает проблему, поскольку она противоречит основному предположению линейной регрессии. Наличие мультиколлинеарности не влияет на предсказательную способность модели. Итак, если вам нужны только прогнозы, наличие мультиколлинеарности не повлияет на ваш результат. Однако, если вы хотите извлечь некоторые идеи из модели и применить их, скажем, в какой-то бизнес-модели, это может вызвать проблемы.
Одна из основных проблем, вызванных мультиколлинеарностью, заключается в том, что она приводит к неверным интерпретациям и дает неверные выводы. Коэффициенты линейной регрессии предполагают среднее изменение целевого значения, если признак изменяется на одну единицу. Таким образом, если существует мультиколлинеарность, это неверно, поскольку изменение одного признака приведет к изменениям коррелированной переменной и последующим изменениям целевой переменной. Это приводит к неправильному пониманию и может привести к опасным результатам для бизнеса.
Очень эффективным способом борьбы с мультиколлинеарностью является использование VIF (фактор инфляции дисперсии). Чем выше значение VIF для признака, тем более линейно коррелирует этот признак. Просто удалите функцию с очень высоким значением VIF и повторно обучите модель на оставшемся наборе данных.
10. Что такое нормальная форма (уравнение) линейной регрессии? Когда следует отдать предпочтение методу градиентного спуска?
Нормальное уравнение линейной регрессии:
β=(X T X) -1 . Х Т Г
Здесь Y=β T X — модель линейной регрессии,
Y — целевая или зависимая переменная,
β — вектор коэффициента регрессии, полученный с помощью нормального уравнения,
X — это матрица признаков, содержащая все признаки в виде столбцов.
Обратите внимание, что первый столбец в матрице X состоит из всех единиц. Это должно включать значение смещения для линии регрессии.
Сравнение градиентного спуска и нормального уравнения:
| Градиентный спуск | Нормальное уравнение |
| Требуется настройка гиперпараметров для альфы (параметр обучения) | Нет такой необходимости |
| Это итеративный процесс | Это неитеративный процесс |
| O(kn 2 ) временная сложность | O(n 3 ) временная сложность из-за оценки X T X |
| Предпочтительно, когда n чрезвычайно велико | Становится довольно медленным для больших значений n |
Здесь « k » — максимальное количество итераций для градиентного спуска, а « n » — общее количество точек данных в обучающем наборе.
Ясно, что если у нас есть большие обучающие данные, нормальное уравнение использовать не рекомендуется. Для малых значений ' n ' нормальное уравнение работает быстрее, чем градиентный спуск.
Что такое машинное обучение и почему это важно
11. Вы запускаете регрессию на разных подмножествах ваших данных, и в каждом подмножестве значение бета для определенной переменной сильно различается. В чем тут может быть дело?
Этот случай подразумевает, что набор данных неоднороден. Таким образом, чтобы преодолеть эту проблему, набор данных должен быть сгруппирован в разные подмножества, а затем для каждого кластера должны быть построены отдельные модели. Другой способ решить эту проблему — использовать непараметрические модели, такие как деревья решений, которые могут достаточно эффективно работать с разнородными данными.

12. Ваша линейная регрессия не работает и сообщает, что существует бесконечное количество лучших оценок для коэффициентов регрессии. Что может быть не так?
Это условие возникает, когда существует идеальная корреляция (положительная или отрицательная) между некоторыми переменными. В этом случае однозначного значения коэффициентов нет, а значит, возникает заданное условие.
13. Что вы подразумеваете под скорректированным R 2 ? Чем он отличается от R2 ?
Скорректированный R 2 , как и R 2 , представляет количество точек, лежащих вокруг линии регрессии. То есть он показывает, насколько хорошо модель соответствует обучающим данным. Формула для скорректированного R 2 является -
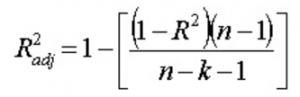
Здесь n — количество точек данных, а k — количество признаков.
Один недостаток R 2 заключается в том, что она всегда будет увеличиваться с добавлением новой функции, независимо от того, полезна ли новая функция или нет. Скорректированный R 2 преодолевает этот недостаток. Значение скорректированного R 2 увеличивается только в том случае, если вновь добавленный признак играет существенную роль в модели.
14. Как вы интерпретируете кривую невязок и подобранных значений?
График остатка по сравнению с подобранным значением используется, чтобы увидеть, имеют ли прогнозируемые значения и остатки корреляцию или нет. Если остатки распределены нормально, со средним значением вокруг подобранного значения и постоянной дисперсией, наша модель работает нормально; в противном случае есть некоторая проблема с моделью.
Наиболее распространенной проблемой, которую можно обнаружить при обучении модели на большом диапазоне набора данных, является гетероскедастичность (это объясняется в ответе ниже). Наличие гетероскедастичности можно легко увидеть, построив кривую зависимости остатка от подогнанного значения.
15. Что такое гетероскедастичность? Каковы последствия и как с этим справиться?
Случайная величина называется гетероскедастичной, если разные подгруппы имеют разную изменчивость (стандартное отклонение).
Существование гетероскедастичности порождает определенные проблемы в регрессионном анализе, поскольку в допущении говорится, что члены ошибки некоррелированы и, следовательно, дисперсия постоянна. Присутствие гетероскедастичности часто можно увидеть в виде конусообразной диаграммы рассеяния для остаточных и подобранных значений.
Одно из основных предположений линейной регрессии состоит в том, что в данных отсутствует гетероскедастичность. Из-за нарушения предположений оценщики с помощью обычных наименьших квадратов (OLS) не являются лучшими линейными несмещенными оценщиками (BLUE). Следовательно, они не дают наименьшей дисперсии, чем другие линейные несмещенные оценки (LUE).
Не существует фиксированной процедуры преодоления гетероскедастичности. Однако есть некоторые способы, которые могут привести к снижению гетероскедастичности. Они есть -
- Логарифмирование данных: экспоненциально возрастающий ряд часто приводит к повышенной изменчивости. Это можно преодолеть с помощью преобразования журнала.
- Использование взвешенной линейной регрессии. Здесь метод OLS применяется к взвешенным значениям X и Y. Один из способов — присвоить веса, непосредственно связанные с величиной зависимой переменной.
16. Что такое ВИФ? Как вы это вычисляете?
Коэффициент инфляции дисперсии (VIF) используется для проверки наличия мультиколлинеарности в наборе данных. Он рассчитывается как —
Здесь VIF j — значение VIF для j -й переменной,
Р j 2 является значением R 2 модели, когда эта переменная подвергается регрессии по отношению ко всем другим независимым переменным.
Если значение VIF велико для переменной, это означает, что R 2 значение соответствующей модели велико, т. е. другие независимые переменные могут объяснить эту переменную. Проще говоря, переменная линейно зависит от некоторых других переменных.
17. Откуда вы знаете, что линейная регрессия подходит для любых заданных данных?
Чтобы увидеть, подходит ли линейная регрессия для любых данных, можно использовать точечный график. Если взаимосвязь выглядит линейной, мы можем выбрать линейную модель. Но если это не так, мы должны применить некоторые преобразования, чтобы сделать связь линейной. Построение графиков рассеяния легко в случае простой или одномерной линейной регрессии. Но в случае многомерной линейной регрессии могут быть построены двумерные попарные графики рассеяния, вращающиеся графики и динамические графики.
18. Как проверка гипотез используется в линейной регрессии?
Проверка гипотез может проводиться в линейной регрессии для следующих целей:
- Чтобы проверить, является ли предиктор значимым для предсказания целевой переменной. Два распространенных метода для этого:
- С помощью p-значений:
Если p-значение переменной больше определенного предела (обычно 0,05), переменная не имеет значения в прогнозе целевой переменной. - Проверяя значения коэффициента регрессии:
Если значение коэффициента регрессии, соответствующего предиктору, равно нулю, эта переменная не имеет значения в прогнозе целевой переменной и не имеет с ней линейной связи.
- С помощью p-значений:
- Чтобы проверить, являются ли рассчитанные коэффициенты регрессии хорошими оценками фактических коэффициентов.
19. Объясните градиентный спуск применительно к линейной регрессии.
Градиентный спуск — это алгоритм оптимизации. В линейной регрессии он используется для оптимизации функции стоимости и поиска значений βs (оценщиков), соответствующих оптимизированному значению функции стоимости.
Градиентный спуск работает как мяч, катящийся по графику (игнорируя инерцию). Мяч движется по направлению наибольшего градиента и останавливается на плоской поверхности (минимумы). 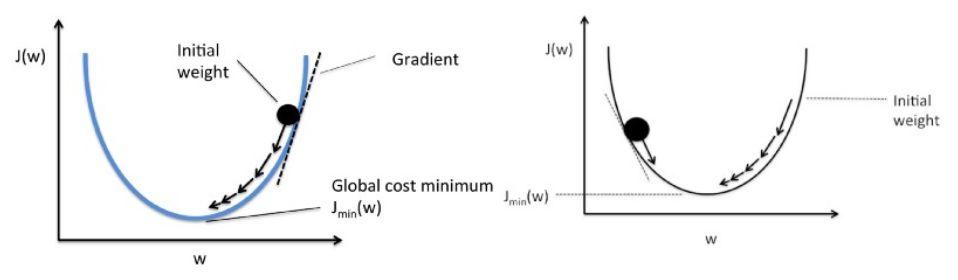
Математически цель градиентного спуска для линейной регрессии состоит в том, чтобы найти решение уравнения
ArgMin J(Θ 0 , Θ 1 ), где J(Θ 0 , Θ 1 ) — функция стоимости линейной регрессии. Это дано — 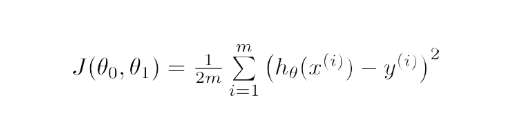
Здесь h — модель линейной гипотезы, h=Θ 0 + Θ 1 x, y — истинный результат, а m — количество точек данных в обучающем наборе.
Градиентный спуск начинается со случайного решения, а затем в зависимости от направления градиента решение обновляется до нового значения, где функция стоимости имеет меньшее значение.
Обновление:
Повторять до схождения 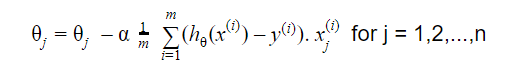
20. Как вы интерпретируете модель линейной регрессии?
Модель линейной регрессии довольно легко интерпретировать. Модель имеет следующий вид: 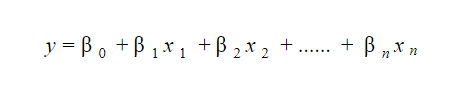
Значение этой модели заключается в том, что можно легко интерпретировать и понять предельные изменения и их последствия. Например, если значение x 0 увеличивается на 1 единицу, сохраняя неизменными другие переменные, общее увеличение значения y составит β i . Математически член пересечения ( β 0 ) является ответом, когда все члены предиктора установлены равными нулю или не учитываются.
Эти 6 методов машинного обучения улучшают здравоохранение
21. Что такое робастная регрессия?
Регрессионная модель должна быть надежной по своей природе. Это означает, что при изменении нескольких наблюдений модель не должна кардинально меняться. Кроме того, на него не должны сильно влиять выбросы.
Модель регрессии с OLS (Обычные наименьшие квадраты) весьма чувствительна к выбросам. Чтобы преодолеть эту проблему, мы можем использовать метод WLS (взвешенных наименьших квадратов) для определения оценок коэффициентов регрессии. Здесь меньший вес придается выбросам или точкам с высоким рычагом в фитинге, что делает эти точки менее значимыми.
22. Какие графики рекомендуется наблюдать перед подгонкой модели?
Перед подгонкой модели необходимо хорошо знать данные, например, каковы тенденции, распределение, асимметрия и т. д. в переменных. Для наблюдения за распределением переменных можно использовать такие графики, как гистограммы, ящичные диаграммы и точечные диаграммы. Помимо этого, необходимо также проанализировать, какова связь между зависимыми и независимыми переменными. Это можно сделать с помощью точечных диаграмм (в случае одномерных задач), вращающихся диаграмм, динамических диаграмм и т. д.
23. Что такое обобщенная линейная модель?
Обобщенная линейная модель является производной от обычной модели линейной регрессии. GLM является более гибким с точки зрения остатков и может использоваться там, где линейная регрессия не кажется подходящей. GLM допускает распределение остатков, отличное от нормального распределения. Он обобщает линейную регрессию, позволяя линейной модели связать целевую переменную с помощью функции связывания. Оценка модели выполняется с использованием метода оценки максимального правдоподобия.
24. Объясните компромисс между смещением и дисперсией.
Смещение относится к разнице между значениями, предсказанными моделью, и реальными значениями. Это ошибка. Одной из целей алгоритма ML является низкое смещение.
Дисперсия относится к чувствительности модели к небольшим колебаниям в обучающем наборе данных. Еще одна цель алгоритма ML — иметь низкую дисперсию.
Для набора данных, который не является точно линейным, невозможно одновременно иметь низкий уровень смещения и дисперсии. Прямолинейная модель будет иметь низкую дисперсию, но высокое смещение, тогда как полином высокой степени будет иметь низкое смещение, но высокую дисперсию.
В машинном обучении невозможно избежать взаимосвязи между предвзятостью и дисперсией.
- Уменьшение смещения увеличивает дисперсию.
- Уменьшение дисперсии увеличивает смещение.
Итак, между ними есть компромисс; специалист по машинному обучению должен решить, исходя из поставленной задачи, насколько можно допустить предвзятость и дисперсию. На основе этого строится окончательная модель.
25. Как кривые обучения могут помочь создать лучшую модель?
Кривые обучения указывают на наличие переобучения или недообучения.
На кривой обучения ошибка обучения и ошибка перекрестной проверки отображаются в зависимости от количества точек обучающих данных. Типичная кривая обучения выглядит следующим образом: 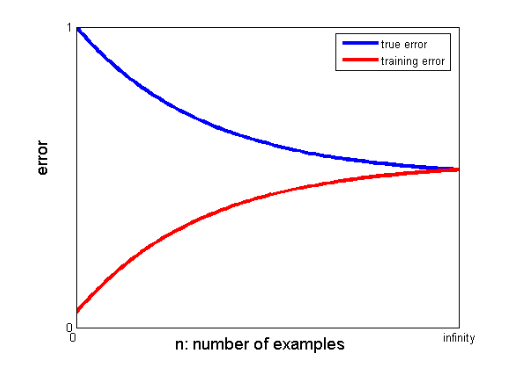
Если ошибка обучения и истинная ошибка (ошибка перекрестной проверки) сходятся к одному и тому же значению, а соответствующее значение ошибки велико, это указывает на то, что модель недостаточно подходит и страдает от высокого смещения.
Интервью по машинному обучению и как их пройти
Интервью по машинному обучению могут различаться в зависимости от типов или категорий, например, некоторые рекрутеры задают много вопросов для интервью по линейной регрессии . Собираясь на роль инженера по машинному обучению, они могут специализироваться на таких категориях, как кодирование, исследования, тематическое исследование, управление проектами, презентация, системный дизайн и статистика. Мы сосредоточимся на наиболее распространенных типах категорий и на том, как к ним подготовиться.
- Кодирование
Кодирование и программирование являются важными компонентами собеседования по машинному обучению и часто используются для отбора кандидатов. Чтобы хорошо пройти эти собеседования, вам нужно иметь хорошие навыки программирования. Интервью по программированию обычно длятся от 45 до 60 минут и состоят всего из двух вопросов. Интервьюер задает тему и ожидает, что заявитель рассмотрит ее в кратчайшие сроки.
Как подготовиться. Вы можете подготовиться к этим собеседованиям, хорошо разбираясь в структурах данных, сложностях времени и пространства, управленческих навыках и способности понять и решить проблему. У upGrad есть отличный курс по разработке программного обеспечения, который может помочь вам улучшить свои навыки программирования и успешно пройти собеседование.
2. Машинное обучение
Ваше понимание машинного обучения будет оцениваться посредством интервью. Сверточные слои, рекуррентные нейронные сети, генеративные противоборствующие сети, распознавание речи и другие темы могут быть затронуты в зависимости от потребностей занятости.
Как подготовиться. Чтобы успешно пройти это собеседование, вы должны убедиться, что у вас есть полное представление о рабочих ролях и обязанностях. Это поможет вам определить спецификации машинного обучения, которые вы должны изучить. Однако, если вы не столкнетесь с какими-либо спецификациями, вы должны глубоко понять основы. Углубленный курс по машинному обучению, который предлагает upGrad, может помочь вам в этом. Вы также можете изучить последние статьи по машинному обучению и искусственному интеллекту, чтобы понять их последние тенденции, и вы можете использовать их на регулярной основе.
3. Скрининг
Это интервью несколько неформальное и, как правило, является одним из начальных пунктов интервью. Потенциальный работодатель часто справляется с этим. Основная цель этого собеседования — дать соискателю представление о бизнесе, роли и обязанностях. В более неформальной обстановке кандидата также спрашивают об его прошлом, чтобы определить, соответствует ли его сфера интересов занимаемой должности.
Как подготовиться. Это очень нетехническая часть собеседования. Все, что для этого требуется, — это ваша честность и основы вашей специализации в области машинного обучения.
4. Дизайн системы
Такие собеседования проверяют способность человека создать полностью масштабируемое решение от начала до конца. Большинство инженеров настолько озабочены проблемой, что часто упускают из виду более широкую картину. Интервью по проектированию системы требует понимания множества элементов, которые в совокупности создают решение. Эти элементы включают внешний вид, балансировщик нагрузки, кеш и многое другое. Эффективную и масштабируемую сквозную систему легче разработать, если эти вопросы хорошо изучены.
Как подготовиться — понять концепции и компоненты проекта проектирования системы. Используйте примеры из реальной жизни, чтобы объяснить структуру вашему интервьюеру, чтобы лучше понять проект.
Популярные блоги о машинном обучении и искусственном интеллекте
| Интернет вещей: история, настоящее и будущее | Учебное пособие по машинному обучению: Изучите машинное обучение | Что такое алгоритм? Просто и легко |
| Заработная плата инженера-робототехника в Индии: все роли | Один день из жизни инженера по машинному обучению: что они делают? | Что такое IoT (Интернет вещей) |
| Перестановка против комбинации: разница между перестановкой и комбинацией | 7 основных тенденций в области искусственного интеллекта и машинного обучения | Машинное обучение с R: все, что вам нужно знать |

Если существует значительный разрыв между сходящимися значениями ошибок обучения и перекрестной проверки, т. е. ошибка перекрестной проверки значительно выше, чем ошибка обучения, это говорит о том, что модель переобучает данные обучения и страдает от высокой дисперсии. .
Инженеры по машинному обучению: мифы против реальности
Вот и конец первого раздела этой серии. Оставайтесь на связи для следующей части серии, состоящей из вопросов, основанных на логистической регрессии . Не стесняйтесь оставлять свои комментарии.
Соавтор — Оджас Агарвал
Вы можете проверить нашу программу Executive PG в области машинного обучения и искусственного интеллекта , которая включает практические семинары, индивидуального отраслевого наставника, 12 тематических исследований и заданий, статус выпускника IIIT-B и многое другое.
Что вы понимаете под регуляризацией?
Регуляризация — это стратегия решения проблемы переобучения модели. Переоснащение происходит, когда сложная модель применяется к обучающим данным. Иногда базовая модель может быть не в состоянии обобщить данные, а сложная модель может переобучить данные. Для решения этой проблемы используется регуляризация. Регуляризация — это процесс добавления членов-коэффициентов (бета) к задаче минимизации таким образом, что члены наказываются и имеют скромную величину. По сути, это помогает идентифицировать шаблоны данных, а также предотвращает переобучение, предотвращая слишком сложную модель.
Что вы понимаете в фиче-инжиниринге?
Процесс преобразования исходных данных в функции, которые лучше описывают основную проблему для прогнозных моделей, что приводит к повышению точности модели на невидимых данных, известен как разработка функций. С точки зрения непрофессионала, проектирование признаков означает создание дополнительных признаков, которые могут помочь в лучшем понимании и моделировании проблемы. Существует два типа разработки функций: ориентированная на бизнес и управляемая данными. Включение функций с коммерческой точки зрения находится в центре внимания разработки функций, ориентированной на бизнес.
Что такое компромисс между смещением и дисперсией?
Разрыв между прогнозируемыми значениями модели и фактическими значениями называется смещением. Это ошибка. Низкое смещение является одной из целей алгоритма ML. Уязвимость модели к крошечным изменениям в обучающем наборе данных называется дисперсией. Низкая дисперсия — еще одна цель алгоритма машинного обучения. Невозможно иметь как низкое смещение, так и низкую дисперсию в наборе данных, который не является идеально линейным. Дисперсия прямолинейной модели мала, но смещение велико, тогда как дисперсия полинома высокой степени мала, но смещение велико. В машинном обучении связь между предвзятостью и изменчивостью неизбежна.
