Введение в функцию плотности вероятности [формула, свойства, приложения, примеры]

Функция плотности вероятности (PDF) — это выражение в статистике, обозначающее распределение вероятностей дискретной случайной величины. Проще говоря, распределение вероятностей можно определить как вероятность результата случайной величины, такой как акции или ETF. Дискретные переменные встречаются в отличие от непрерывной случайной величины, точное значение которой можно определить.

Например, стоимость сума на фондовом рынке имеет только два десятичных знака (например, 65,76) в дискретной случайной величине вместо непрерывной переменной с любым количеством десятичных знаков (пример: 65,7685434567).

Функция плотности вероятности — это статистический инструмент, используемый для определения вероятности результата дискретной случайной величины. На графике PDF выглядят идентично колоколообразной кривой, в которой площадь под кривой представляет вероятность результата.

При проецировании в виде графической модели площадь под кривой представляет собой диапазон, в который попадают значения дискретных случайных величин. Таким образом, общая площадь под кривой равна вероятности исхода переменной.

Функция плотности вероятности может определить вероятность попадания случайной величины в определенный диапазон значений.

Как правило, функции плотности вероятности анализируют риски и потенциальный доход, связанные с конкретным фондом на фондовом рынке.

Условия, которым должна удовлетворять функция, которая считается функцией плотности вероятности

Значение дискретной переменной можно точно измерить, в отличие от непрерывной переменной, которая может иметь бесконечное число значений. Любая функция должна удовлетворять следующим двум условиям, чтобы быть функцией плотности вероятности:

• Значение f(x) для каждого возможного значения случайной величины должно быть положительным (неотрицательным).
• Интегральное значение общей площади кривой (интеграл всех возможных значений случайной величины) должно быть равно 1.

Разница между функцией плотности вероятности и функцией распределения вероятности

Случайные переменные могут иметь много значений. Описание каждого возможного значения, которое может иметь случайная величина, называется ее распределением вероятностей.

Распределение вероятностей дает набор исходов и связанных с ними вероятностей. Статистическая функция, представляющая непрерывное распределение вероятностей, известна как функция плотности вероятности.

Существует еще один статистический инструмент, представляющий дискретное распределение вероятностей, называемый функцией массы вероятности. Это дает подробный отчет обо всех возможных исходах и их вероятности правдоподобия.

Выражение для функций плотности вероятности

Если случайная величина является дискретной, ее распределение вероятности называется функцией массы вероятности, а если это непрерывная величина, то распределение вероятности называется функцией плотности вероятности.

PDF используется, когда рассматриваемая случайная величина имеет диапазон возможных значений. Их распределение вероятностей используется для определения точного значения.

Пусть случайная величина обозначается через X. Функция плотности вероятности f случайной величины X может быть выражена как

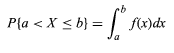
• Значение случайной величины лежит между a и b.
• Если X обозначает вероятность выбора определенного числа из диапазона (интервала) r и s, то функция плотности вероятности может быть выражена как

ж ( Икс ) знак равно 1 / ( s - р ) для р < Икс < s и f ( Икс ) = 0 для Икс < р или Икс > s .

• PDF F представлен как:

F ( Икс ) знак равно п { Икс ≤ Икс }

которая называется функцией распределения или кумулятивной функцией распределения X.

Учитывая, что случайная величина X имеет функцию распределения вероятностей f ( x ), тогда связь между f и F может быть установлена ​​как

F ′(. x ) = f ( x )

Функция распределения дискретной случайной величины отличается от ее функции распределения вероятностей. Связь между ними может быть выражена следующим образом:

Ожидание случайной величины обозначается как

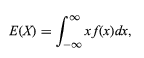
Таким образом, все дискретные и случайные величины можно рассматривать единообразно с помощью комбинированной теории.

Формула функции плотности вероятности

Вероятность непрерывной случайной величины X при некотором фиксированном значении x всегда равна 0. В этом случае P (X = x) использовать нельзя. Значение X, лежащее между диапазоном значений (a, b), должно быть определено. Для его определения используется следующая формула.

Свойства функции плотности вероятности

Например, непрерывная случайная величина, которая принимает свое значение между диапазоном (a, b), будет оцениваться путем вычисления площади под кривой и оси X, построенной с (a) в качестве ее нижнего предела и (b) в качестве его. верхний предел. Функция плотности вероятности для вышеуказанного представлена ​​как:

Функция плотности вероятности положительна (неотрицательна) для всех возможных значений. Это означает, что f(x)≥ 0 для каждого x. Площадь между кривой плотности и осью X (горизонтальная ось) равна 1.

Это также может быть обозначено как:

Кривая функции плотности непрерывна во всем заданном диапазоне, который четко выделяется на фоне ряда непрерывных значений или области определения переменной.

Присоединяйтесь к онлайн-курсу по машинному обучению в ведущих университетах мира — магистерским программам, программам последипломного образования для руководителей и программам повышения квалификации в области машинного обучения и искусственного интеллекта, чтобы ускорить свою карьеру.

Приложения функции плотности вероятности

• Функция плотности вероятности используется при годовом моделировании уровней концентрации NO в атмосфере.
• Моделирование сгорания дизельного двигателя.
• В статистике функция плотности вероятности используется для определения возможностей исхода случайной величины.

Примеры функции плотности вероятности

• Пример 1

Ниже приведен пример использования функции плотности вероятности (PDF) для определения потенциального риска инвестора на фондовом рынке:

Во-первых, PDF-файлы создаются как графический инструмент на основе исторической информации.

Наиболее распространенной формой PDF является нейтральная проекция, в которой риск равен вознаграждению по целому ряду возможностей. Инвесторы с меньшей способностью идти на риск будут вознаграждены только ограниченной прибылью, и, следовательно, они попадают под левую сторону кривой нормального распределения. И наоборот, инвесторы с высокими способностями к риску, скорее всего, будут вознаграждены более высокой доходностью и, следовательно, попадут под правую сторону кривой.

Большинство инвесторов попадают под среднюю способность к риску и, следовательно, занимают середину кривой.

Это помогает в анализе категории инвесторов на основе полученных данных. Это помогает брокерам фондового рынка определить свою целевую категорию клиентов для продажи своей продукции.

• Пример 2

Одним из важных приложений функции плотности вероятности является случайная величина Гаусса, также известная как нормальная случайная величина.

В обоих случаях график представляет собой колоколообразную кривую для функции плотности вероятности.

Плотность может быть выражена как

График приведенного выше уравнения плотности приведен ниже.

Площадь под кривой представляет фактическое значение гауссовой случайной величины.

Заключение

Функция плотности вероятности играет жизненно важную роль в машинном обучении. Студентам, планирующим карьеру в области машинного обучения и искусственного интеллекта, мы настоятельно рекомендуем зарегистрироваться в программе upGrad IIT-Advanced Certificate Program in Machine Learning . Программа настроена и предназначена для того, чтобы вооружить старших работающих специалистов для развертывания моделей машинного обучения с использованием технологии облачных вычислений.

Учебная программа разработана преподавателями IIT Madras и отраслевыми экспертами, чтобы сделать процесс обучения более актуальным и практичным. Программа предлагает всемирно признанную сертификацию от престижного инженерного колледжа № 1 в Индии и комплексную поддержку при трудоустройстве от upGrad.

Более того, вы получаете множество возможностей для совместной работы над крупномасштабными проектами с платной базой учащихся upGrad, насчитывающей более 40 000 человек.

Заходите на наш сайт, чтобы начать свое обучение!