Введение в многомерную регрессию в машинном обучении: полное руководство

Ни для кого не секрет, что современные технологии основаны на данных. Данные могут быть только набором цифр, но их можно осмысленно обрабатывать для извлечения производительности и изобретательности, чтобы предприятия оставались конкурентоспособными и устойчивыми в долгосрочной перспективе. Как оказалось, анализ данных — это ответ на получение точных оценок на основе необработанной информации.

Анализ данных — это метод, который включает в себя статистические и логические идеи для тщательного изучения, обработки и преобразования данных в пригодную для использования форму. Решения, полученные в результате анализа данных, используются в бизнесе для принятия жизненно важных решений. Наука о данных наряду с анализом данных используется для прогнозирования будущих результатов с высокой точностью. Это процесс использования научных методов и алгоритмов для получения достоверной информации из массива данных.

Распространенной проблемой, с которой сталкиваются специалисты по данным, является способ определения наличия статистической связи между переменной ответа (обозначается Y) и независимыми переменными (обозначается Xi).

Ответом на этот вопрос является регрессионный анализ. Давайте разберемся в этом подробнее.

Что такое регрессионный анализ?

Регрессионный анализ — один из популярных методов анализа данных, который следует контролируемому или контролируемому алгоритму машинного обучения. Это эффективный метод выявления и установления связи между переменными в данных.

Регрессионный анализ включает в себя сортировку жизнеспособных переменных с использованием математических стратегий, чтобы сделать очень точные выводы об этих отсортированных переменных.

Что такое многомерная регрессия?

Многовариантность — это управляемый или контролируемый алгоритм машинного обучения, который анализирует несколько переменных данных. Это продолжение множественной регрессии, включающее одну зависимую переменную и множество независимых переменных. Результат прогнозируется на основе количества независимых переменных.

Многомерная регрессия вычисляет формулу, которая объясняет одновременную реакцию факторов, присутствующих в переменных, на изменения в других. Они используются для изучения данных в различных областях. Например, в сфере недвижимости многомерная регрессия используется для прогнозирования цены дома на основе нескольких факторов, таких как его местоположение, количество комнат и доступные удобства.

Функция стоимости в многомерной регрессии

Функция стоимости распределяет стоимость по выборкам, когда результат модели отклоняется от наблюдаемых данных. Уравнение функции стоимости представляет собой сумму квадрата разницы между прогнозируемым значением и фактическим значением, деленную на удвоенную длину набора данных.

Вот пример :

Результат :

Источник

Как использовать многомерный регрессионный анализ?

Процессы, задействованные в многомерном регрессионном анализе, включают в себя выбор признаков, разработку признаков, нормализацию признаков, выбор функций потерь, анализ гипотез и создание регрессионной модели.

1. Выбор признаков: это самый важный шаг в многомерной регрессии. Этот процесс, также известный как выбор переменных, включает в себя выбор жизнеспособных переменных для построения эффективных моделей.
2. Нормализация функций: это включает масштабирование функций для поддержания оптимизированного распределения и соотношений данных. Это помогает лучше анализировать данные. Значение всех функций может быть изменено в соответствии с требованиями.
3. Выбор функции потерь и гипотезы : функция потерь используется для прогнозирования ошибок. Функция потерь вступает в игру, когда предсказание гипотезы отличается от фактических цифр. Здесь гипотеза представляет собой значение, предсказанное на основе признака или переменной.
4. Фиксация параметра гипотезы : Параметр гипотезы фиксируется или устанавливается таким образом, чтобы минимизировать функцию потерь и улучшить прогноз.
5. Уменьшение функции потерь . Функция потерь минимизируется за счет создания алгоритма, специально предназначенного для минимизации потерь в наборе данных, что, в свою очередь, облегчает изменение параметров гипотезы. Градиентный спуск является наиболее часто используемым алгоритмом минимизации потерь. Алгоритм также можно использовать для других действий после завершения минимизации потерь.
6. Анализ функции гипотезы . Функцию гипотезы необходимо проанализировать, поскольку она имеет решающее значение для прогнозирования значений. После того, как функция проанализирована, она тестируется на тестовых данных.

Давайте теперь рассмотрим два способа использования многомерной регрессии.

1. Многомерная линейная регрессия

Многомерная линейная регрессия похожа на простую линейную регрессию, за исключением того, что в многомерной линейной регрессии несколько независимых переменных вносят вклад в зависимые переменные, поэтому в расчетах используется несколько коэффициентов.

• Он используется для получения математической зависимости между несколькими случайными величинами. Он объясняет, сколько независимых переменных связано с одной зависимой переменной.
• Детали нескольких независимых переменных используются для точного прогнозирования их влияния на переменную результата.
• Модель многомерной линейной регрессии генерирует зависимость в линейной форме (форма прямой линии) с наилучшей аппроксимацией каждой точки данных.
• Уравнение модели многомерной линейной регрессии:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

где для i=n наблюдений:

Источник

Когда можно использовать линейную регрессию?

Модель линейной регрессии можно использовать только при наличии двух непрерывных переменных, одна из которых является зависимой, а другая независимой.

Независимая переменная используется в качестве параметра для определения значения или результата зависимой переменной.

2. Многомерная логистическая регрессия

Логистическая регрессия — это алгоритм, используемый для прогнозирования бинарного результата на основе нескольких независимых переменных. У бинарного исхода есть две возможности: либо сценарий происходит (обозначается 1), либо не происходит (обозначается 0).

Логистическая регрессия используется при работе с двоичными данными, данными, в которых результат (или зависимая переменная) является дихотомическим.

Где можно использовать логистическую регрессию?

Логистическая регрессия в основном используется для решения проблем классификации. Например, чтобы выяснить, является ли электронное письмо спамом или нет, и является ли конкретная транзакция злонамеренной или нет. В анализе данных он используется для принятия взвешенных решений для минимизации потерь и увеличения прибыли.

Многомерная логистическая регрессия используется, когда есть одна зависимая переменная и несколько результатов. Он отличается от логистической регрессии наличием более двух возможных результатов.

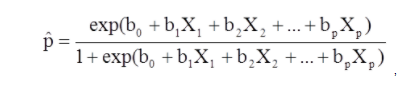
От X1 до Xp — разные независимые переменные.

от b0 до bp — коэффициенты регрессии

Модель множественной логистической регрессии также может быть записана в другой форме. В приведенной ниже форме результат представляет собой ожидаемый логарифм шансов того, что результат присутствует,

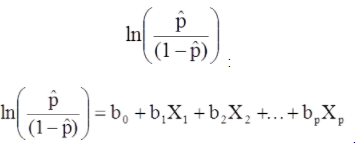
Модель множественной логистической регрессии также может быть записана в другой форме. В приведенной ниже форме результат представляет собой ожидаемый логарифм шансов того, что результат присутствует.

Правая часть приведенного выше уравнения напоминает уравнение линейной регрессии, но метод определения коэффициентов регрессии отличается.

Допущения в модели многомерной регрессии

• Зависимая и независимая переменные имеют линейную зависимость.
• Независимые переменные не имеют сильной корреляции между собой.
• Наблюдения yi выбираются случайным образом и индивидуально из совокупности.

Допущения в модели многомерной логистической регрессии

• Зависимая переменная является номинальной или порядковой. Номинальные переменные имеют две или более категории без какой-либо значимой организации. Порядковые переменные также могут иметь две или более категории, но они имеют структуру и могут быть ранжированы.
• Могут быть одна или несколько независимых переменных, которые могут быть порядковыми, непрерывными или номинальными. Непрерывные переменные — это те, которые могут иметь бесконечные значения в пределах определенного диапазона.
• Зависимые переменные являются взаимоисключающими и исчерпывающими.
• Независимые переменные не имеют сильной корреляции между собой.

Преимущества многомерной регрессии

1. Многомерная регрессия помогает нам изучать отношения между несколькими переменными в наборе данных.
2. Корреляция между зависимыми и независимыми переменными помогает предсказать результат.
3. Это один из самых удобных и популярных алгоритмов, используемых в машинном обучении.

Недостатки многомерной регрессии

• Сложность многомерных методов требует сложных математических расчетов.
• Нелегко интерпретировать выходные данные многомерной регрессионной модели, поскольку в выходных данных потерь и ошибок есть несоответствия.
• Многомерные регрессионные модели нельзя применять к меньшим наборам данных; они предназначены для получения точных результатов, когда речь идет о больших наборах данных.

Если вы хотите узнать больше о многомерной регрессии и других сложных предметах науки о данных, у upGrad есть решение для вас. Наш 18-месячный курс магистра наук в области науки о данных от Ливерпульского университета Джона Мурса охватывает более 500 часов тщательного обучения, 25 коуч-сессий (проводятся в формате 1:8) и более 20 живых сессий. upGrad также предлагает помощь в обучении 1:1 и поддержку профориентации на 360° для студентов, чтобы изменить свою карьеру. Учащиеся могут использовать взаимное обучение на глобальной платформе с более чем 40 000 платных учащихся и работать над совместными проектами по шести функциональным специализациям, чтобы максимизировать свой учебный опыт.