Гауссовский наивный байесовский алгоритм: что вам нужно знать?
Опубликовано: 2021-02-22Оглавление
Гауссовский наивный байесовский метод
Наивный Байес — это вероятностный алгоритм машинного обучения, используемый для многих функций классификации и основанный на теореме Байеса. Гауссовский наивный байесовский метод является расширением наивного байесовского метода. В то время как другие функции используются для оценки распределения данных, гауссово или нормальное распределение проще всего реализовать, поскольку вам нужно будет вычислить среднее значение и стандартное отклонение для обучающих данных.
Что такое наивный байесовский алгоритм?
Наивный байесовский алгоритм — вероятностный алгоритм машинного обучения, который можно использовать в нескольких задачах классификации. Типичными приложениями Наивного Байеса являются классификация документов, фильтрация спама, прогнозирование и так далее. Этот алгоритм основан на открытиях Томаса Байеса, отсюда и его название.
Название «Наивный» используется потому, что алгоритм включает в свою модель функции, которые не зависят друг от друга. Любые изменения значения одной функции не влияют напрямую на значение любой другой функции алгоритма. Основное преимущество алгоритма наивного Байеса заключается в том, что это простой, но мощный алгоритм.
Он основан на вероятностной модели, в которой алгоритм может быть легко закодирован, а прогнозы сделаны быстро в режиме реального времени. Следовательно, этот алгоритм является типичным выбором для решения реальных проблем, поскольку его можно настроить для мгновенного ответа на запросы пользователя. Но прежде чем мы углубимся в Наивный Байес и Гауссовский Наивный Байес, мы должны знать, что подразумевается под условной вероятностью.
Объяснение условной вероятности
Мы можем лучше понять условную вероятность на примере. При подбрасывании монеты вероятность выпадения вперед или решки составляет 50%. Точно так же вероятность получить 4, когда вы бросаете кости с гранями, составляет 1/6 или 0,16.
Если мы возьмем колоду карт, какова вероятность получить даму при условии, что это пика? Поскольку уже задано условие, что это должна быть пика, знаменатель или набор выбора становится равным 13. В пиковой даме есть только одна дама, поэтому вероятность выбора пиковой дамы становится 1/13 = 0,07.

Условная вероятность события А при данном событии В означает вероятность наступления события А при условии, что событие В уже произошло. Математически условная вероятность A при данном B может быть обозначена как P[A|B] = P[A AND B] / P[B].
Рассмотрим небольшой сложный пример. Возьмем школу со 100 учениками. Это население можно разделить на 4 категории: студенты, учителя, мужчины и женщины. Рассмотрим приведенную ниже таблицу:
| Женский | Мужчина | Всего | |
| Учитель | 8 | 12 | 20 |
| Ученик | 32 | 48 | 80 |
| Всего | 40 | 50 | 100 |
Здесь какова условная вероятность того, что некий житель школы является Учителем при условии, что он Человек.
Чтобы рассчитать это, вам придется отфильтровать подгруппу из 60 мужчин и перейти к 12 учителям-мужчинам.
Итак, ожидаемая условная вероятность P[Teacher | Мужчина] = 12/60 = 0,2
P (учитель | мужчина) = P (учитель ∩ мужчина) / P (мужчина) = 12/60 = 0,2
Это может быть представлено как Учитель (A) и Мужчина (B), разделенный на Мужчина (B). Точно так же можно рассчитать условную вероятность B при заданном A. Правило, которое мы используем для наивного Байеса, можно вывести из следующих обозначений:
Р (А | В) = Р (А ∩ В) / Р (В)
P (B | A) = P (A ∩ B) / P (A)
Правило Байеса
В правиле Байеса мы идем от P (X | Y), которое можно найти в обучающем наборе данных, чтобы найти P (Y | X). Для этого все, что вам нужно сделать, это заменить A и B на X и Y в приведенных выше формулах. Для наблюдений X будет известной переменной, а Y будет неизвестной переменной. Для каждой строки набора данных вы должны рассчитать вероятность Y при условии, что X уже произошло.
Но что происходит, когда в Y больше двух категорий? Мы должны вычислить вероятность каждого класса Y, чтобы определить выигрышный.
По правилу Байеса мы идем от P (X | Y), чтобы найти P (Y | X)
Из данных обучения известно: P(X | Y) = P(X ∩ Y) / P(Y)
P (Доказательство | Результат)
Неизвестно – будет предсказано для тестовых данных: P (Y | X) = P (X ∩ Y) / P(X)
P (Исход | Доказательства)

Правило Байеса = P (Y | X) = P (X | Y) * P (Y) / P (X)
Наивный Байес
Правило Байеса дает формулу для вероятности Y при условии X. Но в реальном мире может быть несколько переменных X. Когда у вас есть независимые функции, правило Байеса можно расширить до правила наивного Байеса. X не зависят друг от друга. Наивная формула Байеса более мощная, чем формула Байеса.
Гауссовский наивный байесовский метод
До сих пор мы видели, что X находятся в категориях, но как вычислить вероятности, когда X является непрерывной переменной? Если мы предполагаем, что X следует определенному распределению, вы можете использовать функцию плотности вероятности этого распределения, чтобы вычислить вероятность правдоподобия.
Если мы предполагаем, что X следуют гауссовскому или нормальному распределению, мы должны заменить плотность вероятности нормального распределения и назвать его гауссовым наивным байесовским. Чтобы вычислить эту формулу, вам нужно среднее значение и дисперсия X.
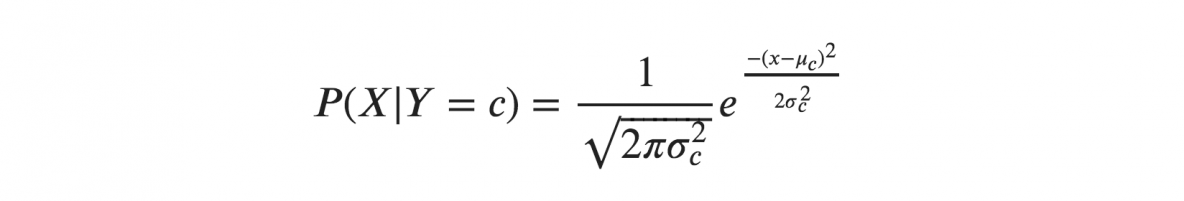
В приведенных выше формулах сигма и мю — это дисперсия и среднее значение непрерывной переменной X, вычисленной для данного класса c функции Y.
Представление для гауссовского наивного Байеса
Приведенная выше формула рассчитывала вероятности входных значений для каждого класса через частоту. Мы можем рассчитать среднее значение и стандартное отклонение x для каждого класса для всего распределения.
Это означает, что наряду с вероятностями для каждого класса мы также должны хранить среднее значение и стандартное отклонение для каждой входной переменной для класса.
среднее (х) = 1/n * сумма (х)
где n представляет количество экземпляров, а x — значение входной переменной в данных.
стандартное отклонение (x) = sqrt (1/n * сумма (xi-mean (x) ^ 2))
Здесь вычисляется квадратный корень из среднего значения различий каждого x и среднего значения x, где n — количество экземпляров, sum() — функция суммы, sqrt() — функция квадратного корня, а xi — конкретное значение x. .

Прогнозы с гауссовой наивной байесовской моделью
Функцию плотности вероятности Гаусса можно использовать для прогнозирования путем замены параметров новым входным значением переменной, и в результате функция Гаусса даст оценку вероятности нового входного значения.
Наивный байесовский классификатор
Наивный байесовский классификатор предполагает, что значение одного признака не зависит от значения любого другого признака. Наивным байесовским классификаторам нужны обучающие данные для оценки параметров, необходимых для классификации. Благодаря простой конструкции и применению наивные байесовские классификаторы подходят для многих реальных сценариев.
Заключение
Гауссовский наивный байесовский классификатор — это быстрый и простой метод классификатора, который очень хорошо работает без особых усилий и с хорошим уровнем точности.
Если вам интересно узнать больше об искусственном интеллекте и машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, Статус выпускника IIIT-B, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.
Изучите курс машинного обучения в лучших университетах мира. Заработайте программы Masters, Executive PGP или Advanced Certificate Programs, чтобы ускорить свою карьеру.
Что такое наивный алгоритм Байеса?
Наивный байесовский алгоритм — классический алгоритм машинного обучения. Берущий свое начало в статистике, наивный байесовский алгоритм представляет собой простой и мощный алгоритм. Наивные байесовские классификаторы — это семейство классификаторов, основанных на применении анализа условной вероятности. В этом анализе условная вероятность события вычисляется с использованием вероятности каждого из отдельных событий, составляющих событие. Наивные байесовские классификаторы часто оказываются чрезвычайно эффективными на практике, особенно когда число измерений набора признаков велико.
Каковы приложения наивного алгоритма Байеса?
Наивный байесовский метод используется при классификации текстов, классификации документов и индексации документов. В наивном байесовском подходе каждому возможному признаку не присваивается вес на этапе предварительной обработки, а веса назначаются позже во время обучения, а также на этапах распознавания. Основное предположение наивного байесовского алгоритма состоит в том, что признаки независимы.
Что такое гауссовский наивный байесовский алгоритм?
Gaussian Naive Bayes — вероятностный алгоритм классификации, основанный на применении теоремы Байеса с сильными предположениями о независимости. В контексте классификации независимость относится к идее о том, что наличие одного значения признака не влияет на наличие другого (в отличие от независимости в теории вероятностей). Наивный относится к использованию предположения о том, что свойства объекта независимы друг от друга. Известно, что в контексте машинного обучения наивные байесовские классификаторы очень выразительны, масштабируемы и достаточно точны, но их производительность быстро ухудшается с ростом обучающей выборки. Успеху наивных байесовских классификаторов способствует ряд особенностей. В частности, они не требуют настройки параметров модели классификации, хорошо масштабируются с размером набора обучающих данных и могут легко обрабатывать непрерывные функции.
