Обновление CSS-анимации с помощью кривых движения

Есть анимация пользовательского интерфейса, а есть хорошая анимация пользовательского интерфейса. Хорошая анимация заставляет вас воскликнуть «Вау!» — плавно, красиво и, главное, естественно, а не блочно, жестко или роботизированно. Если вы часто пользуетесь Dribbble или UpLabs, вы поймете, о чем я говорю.

Дальнейшее чтение о Smashing:

• Анимации SVG и CSS с clip-path
• Практические методы анимации
• Создание «рисованных» анимаций с помощью SVG
• Новый API веб-анимации

С таким количеством замечательных дизайнеров, создающих такие красивые анимации, любой разработчик, естественно, захочет воссоздать их в своих собственных проектах. Теперь CSS предоставляет некоторые предустановки для transition-timing-function , такие как ease-in , ease-out и ease-in-out , которые добавляют некоторый уровень плавности и реализма, но они очень общие, не так ли? Насколько скучно было бы, если бы каждая анимация в Интернете следовала одним и тем же трем временным функциям?

Одним из свойств функции transition-timing-function является cubic-bezier(n1, n2, n3, n4) , в которой вы можете передать четыре числа, чтобы создать свою собственную функцию синхронизации. К концу этой статьи вы будете точно знать, что означают эти четыре числа — и все же, поверьте мне, придумать четыре числа, чтобы зафиксировать переход, который вы представляете в своей голове, совсем не просто. Но благодаря cubic-bezier и Цезарю вам это не нужно. Эти инструменты привносят кривые движения в Интернет.

Кривые движения в основном используются аниматорами (например, в Adobe After Effects) для создания сложных реалистичных анимаций. С cubic-bezier и Цезарем вы можете просто манипулировать формой кривой, и эти четыре числа ( n1, n2, n3, n4 ) будут заполнены для вас, что абсолютно здорово! Тем не менее, чтобы использовать и максимально использовать кривые движения, вам нужно понять, как они работают, и это то, что мы собираемся сделать в этой статье. Давай начнем.

Понимание кривых движения

Кривая движения — это не что иное, как график между любым анимируемым свойством и временем. Кривая движения определяет, как скорость анимации, работающей под ее влиянием, изменяется во времени.

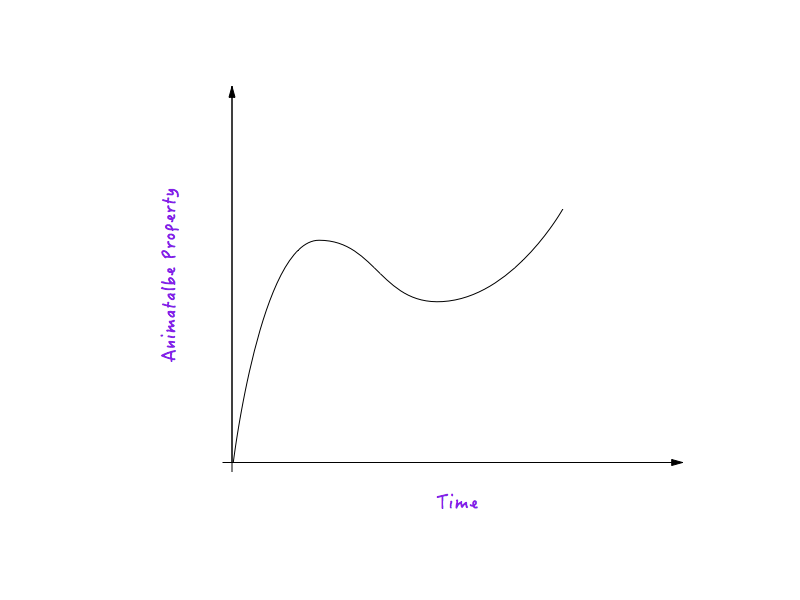
Возьмем Distance ( translateX ) в качестве примера анимируемого свойства. (Объяснение справедливо для любого другого анимируемого свойства.)

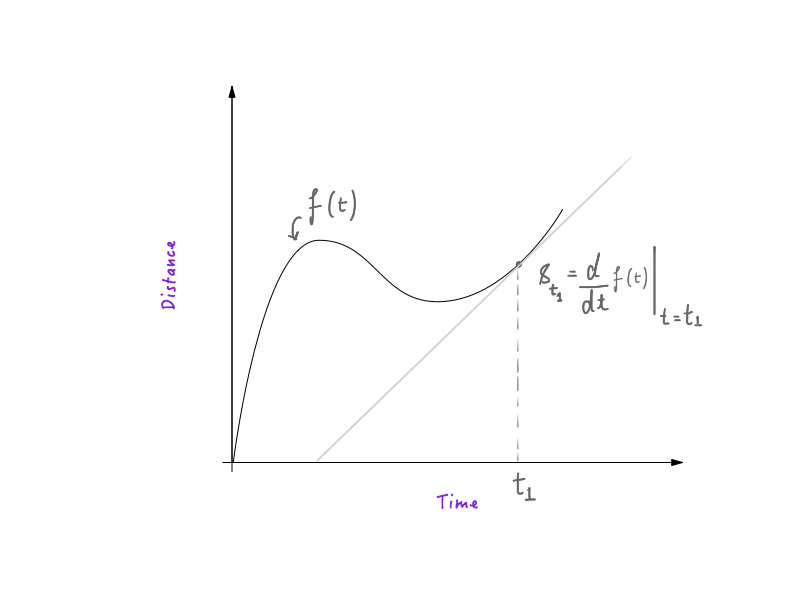
Если у вас есть хоть какой-то опыт работы с физикой и основами исчисления, вы знаете, что вычислить скорость по графику расстояние-время очень просто. Первая производная расстояния как функции времени по времени — это скорость, что означает, что объект, следующий кривой зависимости расстояния от времени, будет иметь большую скорость в местах, где кривая крутая, и меньшую в местах, где кривая более пологая. . Если вы знаете, как это работает, отлично! Все готово, и вы можете перейти к следующему разделу.

Теперь я знаю, что дизайн и разработка — это разные области, и не у всех одинаковый опыт. Возможно, два абзаца выше были для вас жаргоном. Не волнуйтесь. Мы продолжим и разберемся с жаргоном.

Обратите внимание на красную рамку ниже. Давайте возьмем здесь маленькую девчонку и назовем красную коробку «Boxy»; так будет проще обращаться к нему. Итак, Boxy будет линейно двигаться от одного края экрана к другому, и мы проанализируем его движение.

Одна из предустановок функции transition-timing-function — linear . Чтобы заставить Boxy двигаться, все, что мы делаем, это добавляем следующий класс.

 .moveForward { transform: translateX(1000px); }

Чтобы управлять анимацией, мы бы установили свойство transition для Boxy следующим образом:

 #boxy { width: 200px; height: 200px; background: red; transition-property: transform; transition-duration: 1s; transition-timing-function: linear; }

Это очень подробный способ указать transition . На самом деле вы почти всегда найдете transition , записанный в сокращенной форме:

 #boxy { width: 200px; height: 200px; background: red; transition: transform 1s linear; }

Посмотрим, как пойдет.

Роботизированный, не так ли? Можно сказать, что это движение кажется роботизированным, потому что оно линейно, что является вполне правдоподобным ответом. Но не могли бы вы объяснить, почему? Мы видим, что настройка linear приводит к роботизированному движению, но что именно происходит за кулисами? Это то, что мы выясним в первую очередь; мы собираемся добраться до внутренностей и понять, почему это движение кажется роботизированным, блочным и неестественным.

Давайте начнем с построения графика движения Бокси, чтобы посмотреть, сможем ли мы получить некоторое представление. Наш график будет иметь две оси: первая — расстояние, а вторая — время. Boxy преодолевает общее расстояние в 1000 пикселей (расстояние) за 1 секунду (время). Теперь не пугайтесь всей математики ниже — это очень просто.

Вот наш очень простой график с указанными осями.

Сейчас там пусто. Давайте заполним его некоторыми данными.

Для начала мы знаем, что в 0 секунд, когда анимация еще не началась, Boxy находится в исходном положении (0 пикселей). И по прошествии 1 секунды Boxy прошел в общей сложности 1000 пикселей, приземлившись на противоположном краю дисплея.

Нанесем эти данные на график.

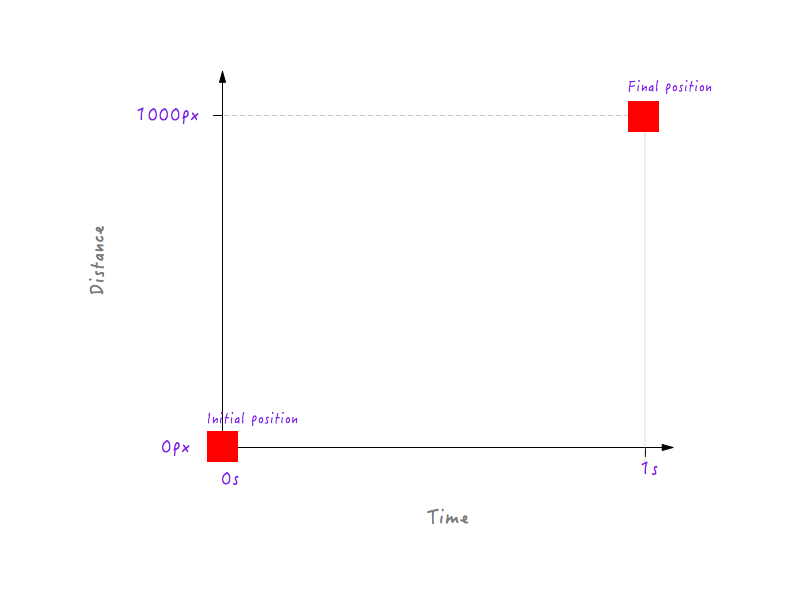
Все идет нормально. Но двух точек данных недостаточно — нам нужно больше. На следующем рисунке показано положение Boxy в разные моменты времени (все благодаря моей высокоскоростной камере).

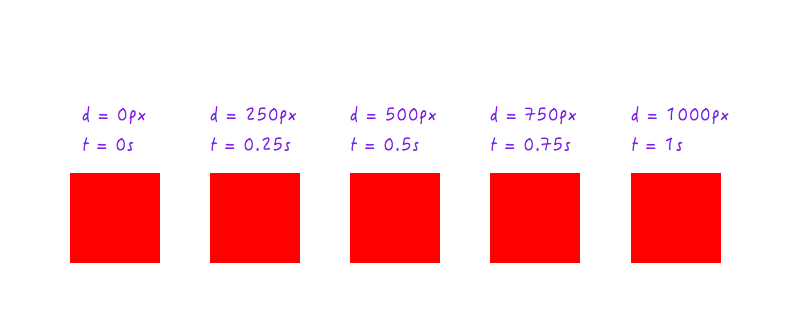
Добавим эти данные на наш график.

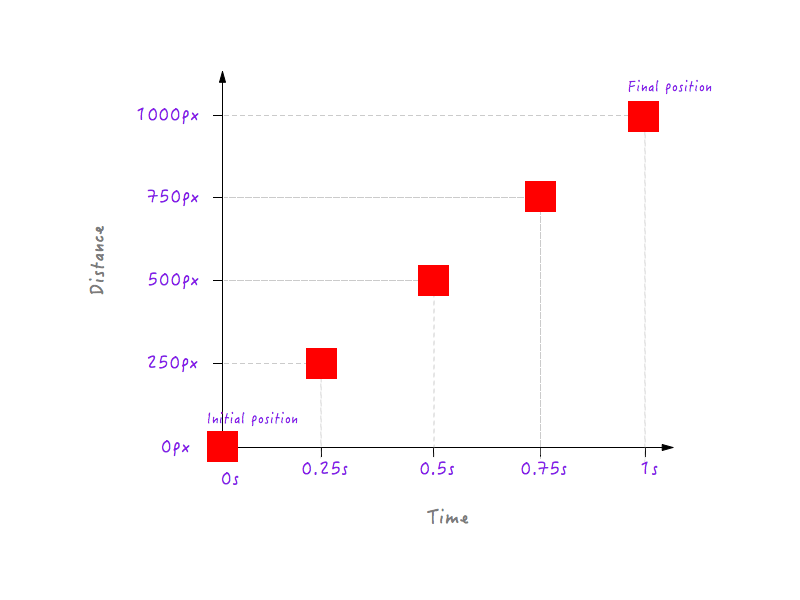
Конечно, вы могли бы иметь гораздо больше точек данных для разных моментов времени (например, 0,375 секунды, 0,6 секунды и т. д.), но того, что у нас есть, достаточно для завершения нашего графика. Соединив все точки, мы завершили график. Дай пять!

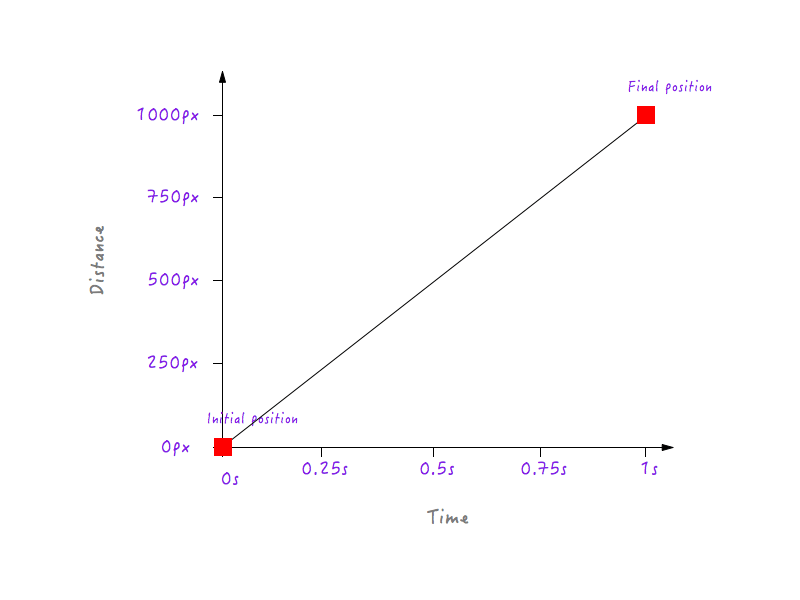
Круто, но что это нам говорит? Помните, мы начали наше расследование с целью понять, почему линейное движение Бокси кажется неестественным и роботизированным? На первый взгляд, этот график, который мы только что построили, ничего нам об этом не говорит. Нам нужно идти глубже.

Помните о графике, и давайте немного поговорим о скорости. Я знаю, что вы знаете, что такое скорость — я просто хотел бы выразить это в математических терминах. Как говорится, формула скорости такова:

Поэтому, если автомобиль преодолевает расстояние 100 километров за 1 час, говорят, что его скорость равна 100 километрам в час.

Если автомобиль удвоит скорость, он начнет преодолевать вдвое большее расстояние (200 километров) за тот же интервал (1 час), или, другими словами, прежний путь в 100 километров он преодолеет вдвое быстрее (0,5 часа). . Есть смысл?

Точно так же, если бы автомобиль уменьшил свою скорость вдвое (то есть замедлился вдвое), он начал бы преодолевать расстояние в 50 километров за тот же интервал (1 час), или, другими словами, он преодолел бы первоначальный путь в 100 км. километров в два раза быстрее (2 часа).

Здорово! С этим по пути, давайте поднимем, где мы остановились. Мы пытались выяснить, как график между расстоянием и временем может помочь нам понять, почему линейное движение Бокси кажется роботизированным.

Эй, подожди секунду! У нас есть график между расстоянием и временем, а скорость можно рассчитать по расстоянию и времени, не так ли? Попробуем рассчитать скорость Бокси в разные промежутки времени.

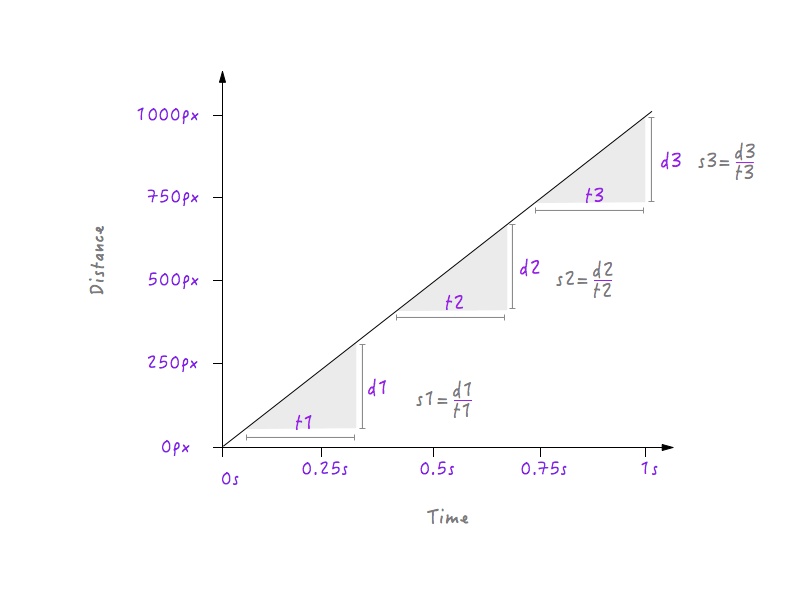
Здесь я выбрал три разных временных интервала: один в начале, один в середине и один в конце рядом с конечной позицией. Как видно, на всех трех интервалах Boxy имеет одинаковую скорость (s1 = s2 = s3) в 1000 пикселей в секунду; то есть независимо от того, какой интервал вы выберете на графике выше, вы обнаружите, что Boxy движется со скоростью 1000 пикселей в секунду. Разве это не странно? Вещи в реальной жизни не движутся с постоянной скоростью; они начинают медленно, постепенно увеличивают свою скорость, двигаются некоторое время, а затем снова замедляются перед остановкой, но Бокси резко стартует со скоростью 1000 пикселей в секунду, двигаясь с той же скоростью и резко останавливаясь точно с той же скоростью. Вот почему движения Бокси кажутся роботизированными и неестественными. Нам придется изменить наш график, чтобы исправить это. Но прежде чем углубляться, нам нужно знать, как изменения скорости повлияют на график, нарисованный между расстоянием и временем. Готовый? Это будет весело.

Давайте удвоим скорость Boxy и посмотрим, как в ответ изменится внешний вид графика. Исходная скорость Boxy, как мы рассчитали выше, составляет 1000 пикселей в секунду. Поскольку мы удвоили скорость, Boxy теперь сможет преодолевать расстояние в 1000 пикселей вдвое быстрее, то есть за 0,5 секунды. Нанесем это на график.

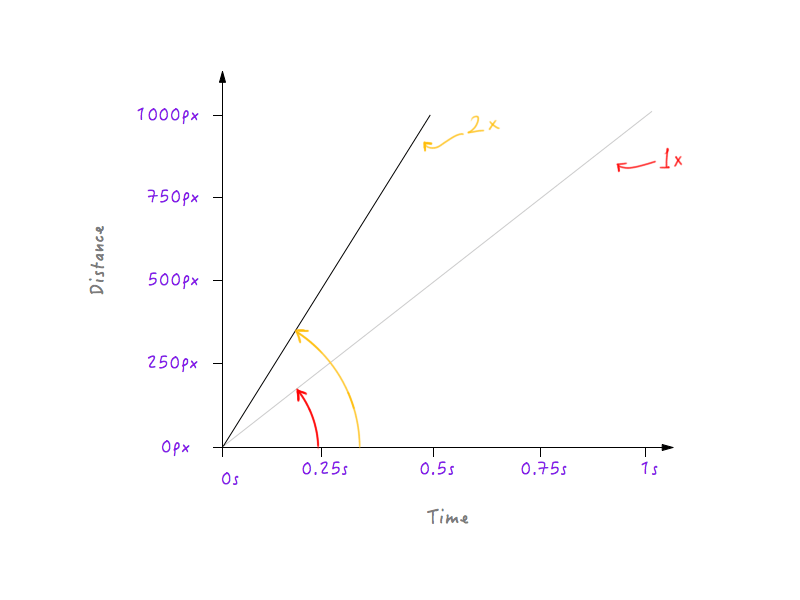
Что, если мы утроим скорость? Теперь Boxy покрывает 1000 пикселей за одну треть времени (треть секунды).

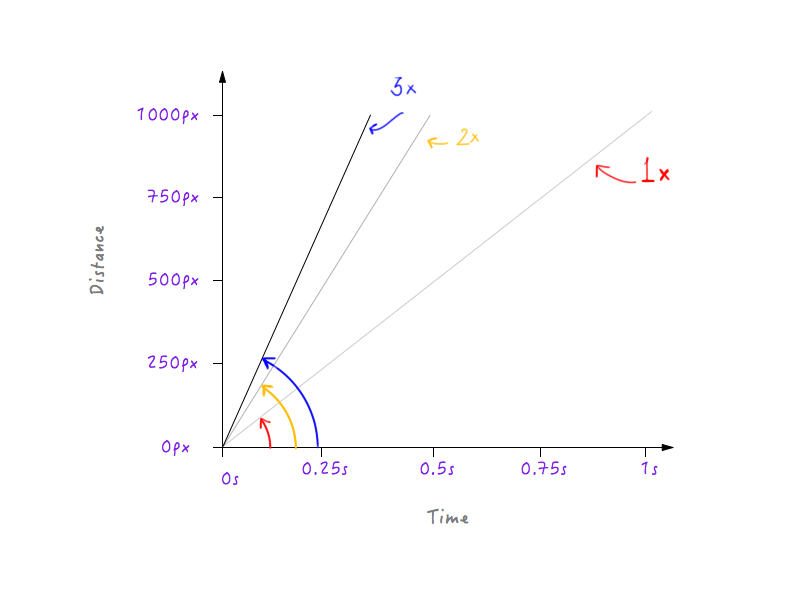
Хм, заметил что-то? Обратите внимание, как при изменении графика угол, который линия образует с осью времени, увеличивается по мере увеличения скорости.

Хорошо, давай уменьшим вдвое скорость Бокси. Уменьшение его скорости вдвое означает, что Boxy сможет покрыть только 500 пикселей (половину исходного расстояния) за 1 секунду. Нанесем это на график.

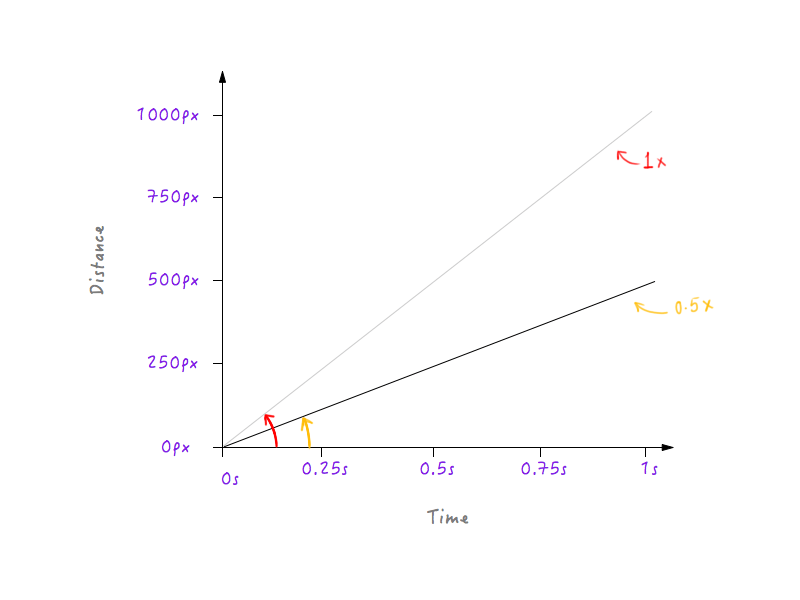
Давайте еще немного замедлим Boxy, сделав скорость в три раза меньше исходной. Бокси сможет преодолеть треть первоначального расстояния за 1 секунду.

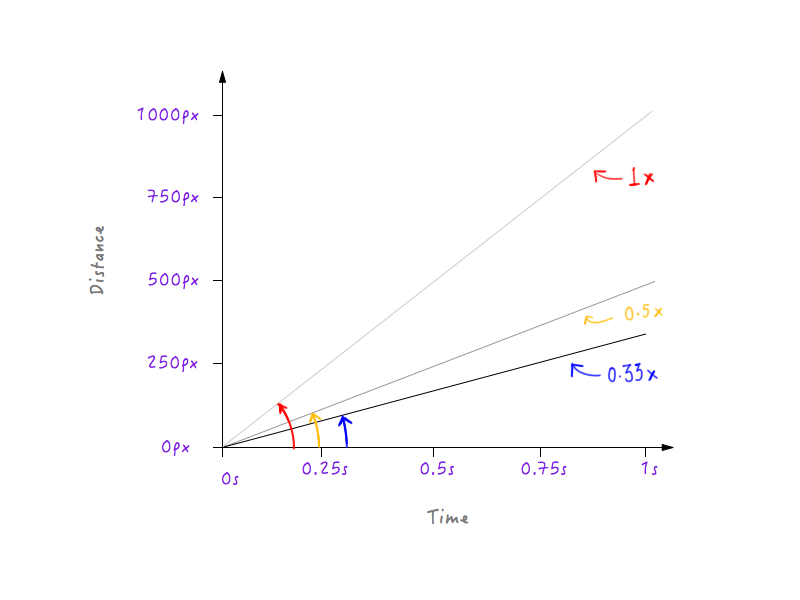
Видите образец? Линия становится все круче и круче по мере того, как мы увеличиваем скорость Бокси, и начинает сглаживаться, когда мы замедляем Бокси.

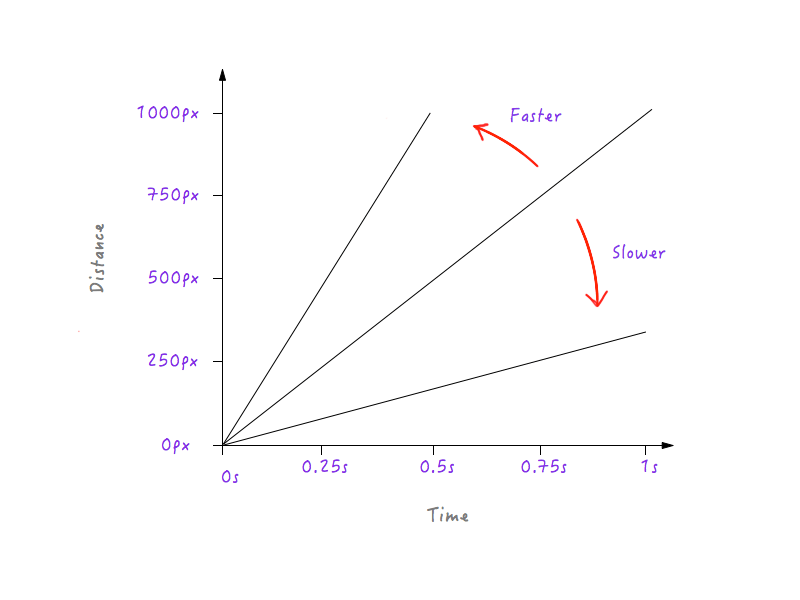
Это имеет смысл, потому что для более крутой линии небольшой сдвиг во времени приводит к гораздо большему изменению расстояния, что подразумевает большую скорость.

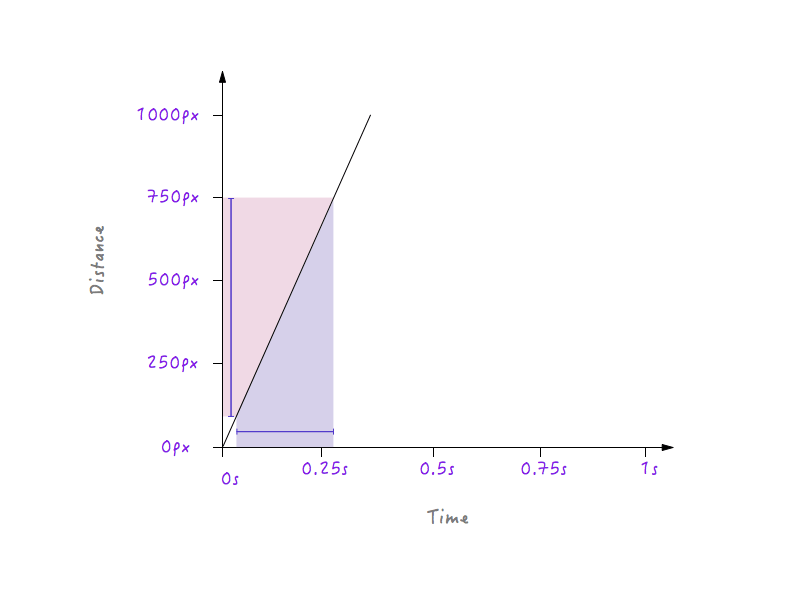
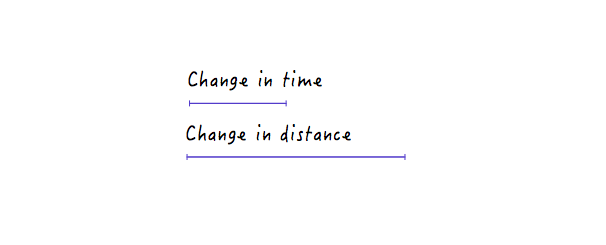
С другой стороны, для менее крутой линии большое изменение во времени вызывает лишь небольшое изменение расстояния, что означает более низкую скорость.

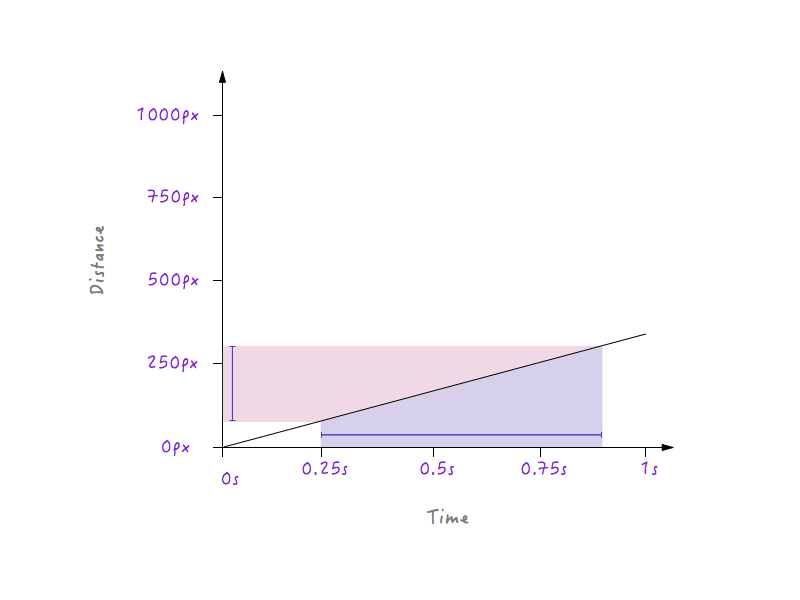
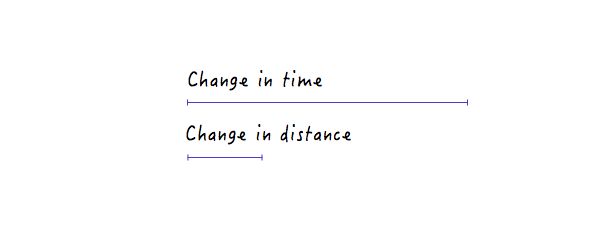
Со всеми изменениями, которые мы внесли, Boxy по-прежнему движется линейно, только с разной скоростью. Однако с нашими недавно полученными знаниями о том, как изменения расстояния во времени могут влиять на скорость, мы можем поэкспериментировать и нарисовать график, который заставляет Бокси двигаться так, чтобы это выглядело естественно и реалистично.

Давайте сделаем это шаг за шагом. Во-первых, в реальной жизни все начинается медленно и медленно набирает скорость. Итак, давайте сделаем это.

Во всех итерациях графика, показанного ниже, вы заметите, что точки в противоположных углах остаются фиксированными. Это связано с тем, что мы не меняем длительность анимации и расстояние, которое проходит Бокси.

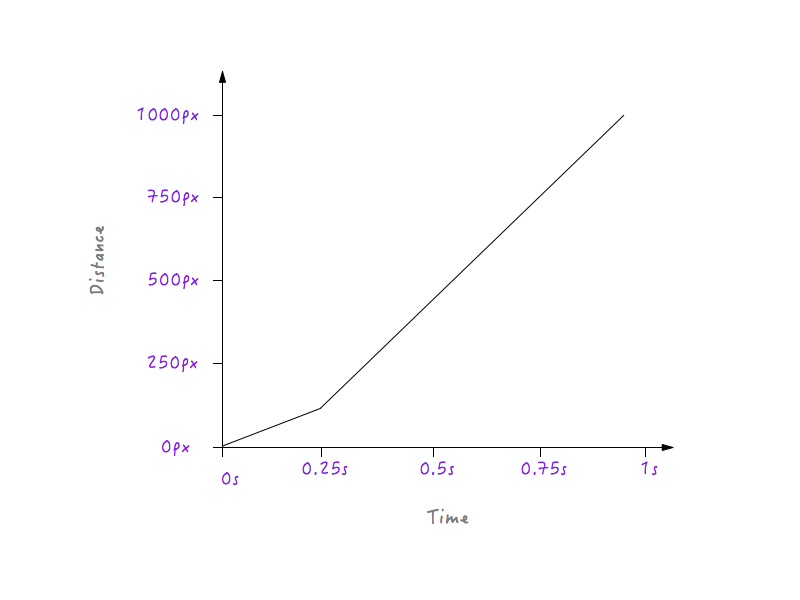
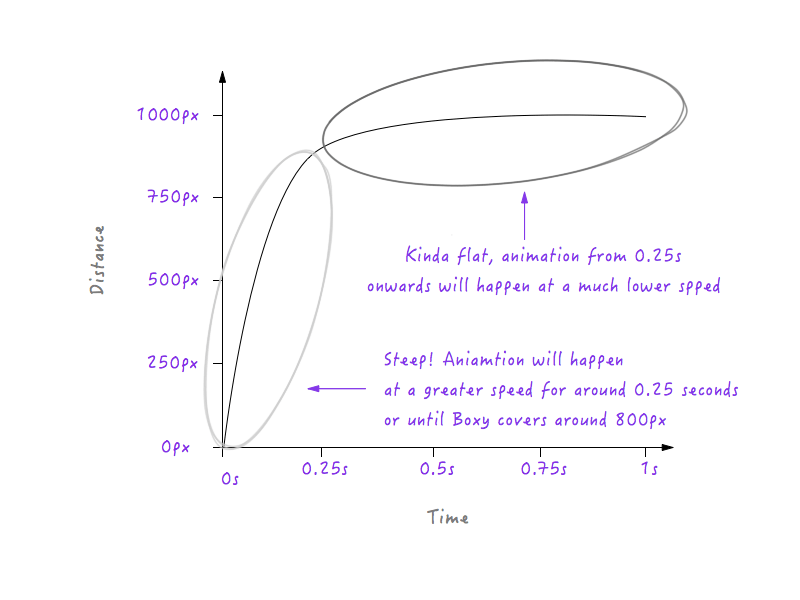
Если Boxy будет следовать приведенному выше графику, он будет двигаться с более низкой скоростью в течение 0,25 секунды, потому что линия менее крутая, начиная с 0 до 0,25 секунды, а затем он резко переключится на более высокую скорость через 0,25 секунды (причина в том, что что линия на графике становится круче через 0,25 секунды). Однако нам нужно будет сгладить этот переход; нам не нужны углы — в конце концов, это называется кривой движения. Превратим этот угол в кривую.

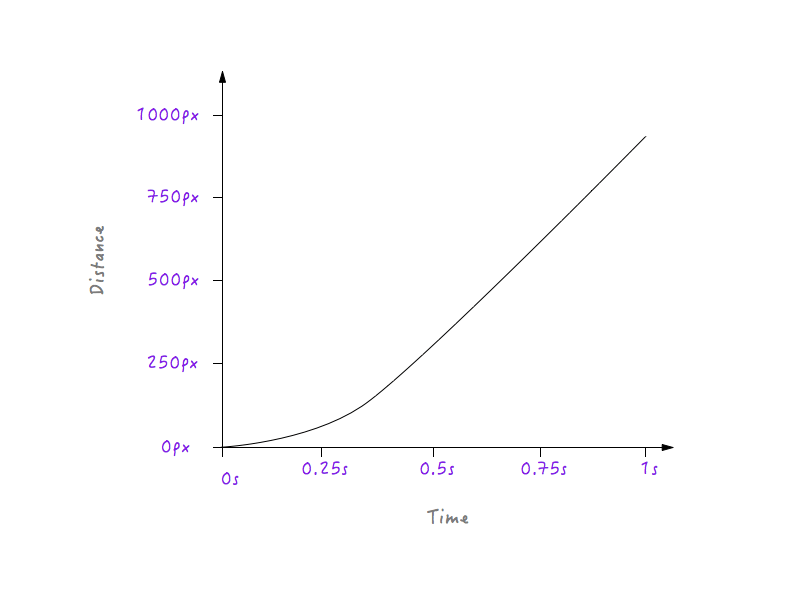
Обратите внимание на плавный переход Boxy от состояния покоя к постепенному увеличению скорости.

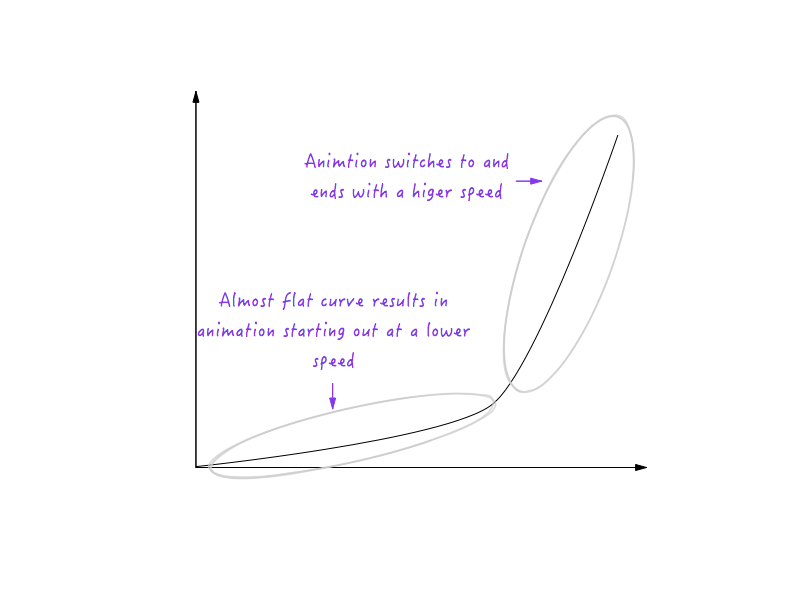
Хорошо! Затем объекты в реальной жизни постепенно замедляются, прежде чем остановиться. Давайте изменим график, чтобы это произошло. Опять же, мы выберем момент времени, после которого мы хотели бы, чтобы Boxy начал замедляться. Как насчет 0,6 секунды? Здесь я уже сгладил угол перехода до кривой.

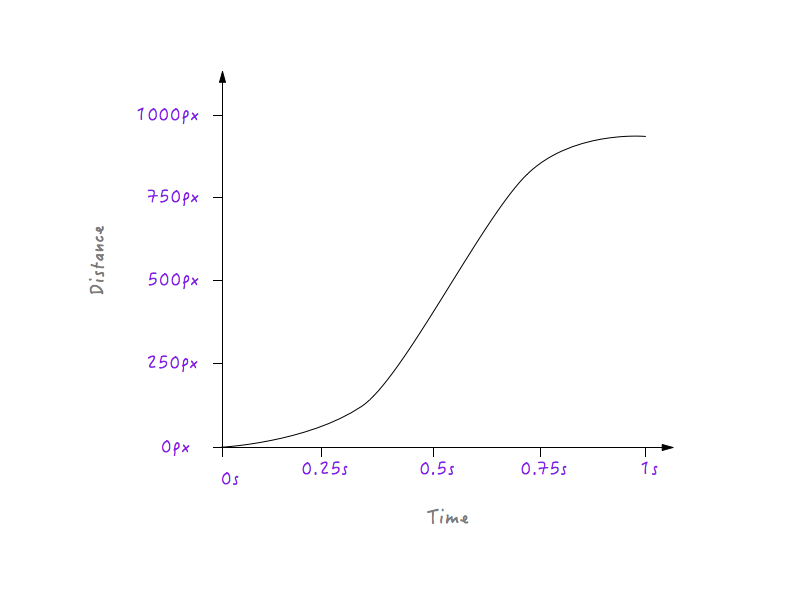
Посмотрите на Бокси вперед! Гораздо естественнее, не так ли?

Кривая, которую мы нарисовали вместо угла, на самом деле представляет собой набор множества маленьких отрезков; и, как вы уже знаете, чем круче линия на графике, тем выше скорость, а чем пологее линия, тем медленнее скорость. Обратите внимание, как в левой части изображения сегменты линии, составляющие кривую, становятся все круче и круче, что приводит к постепенному увеличению скорости, и постепенно уплощаются с правой стороны, что приводит к постепенному снижению скорости?

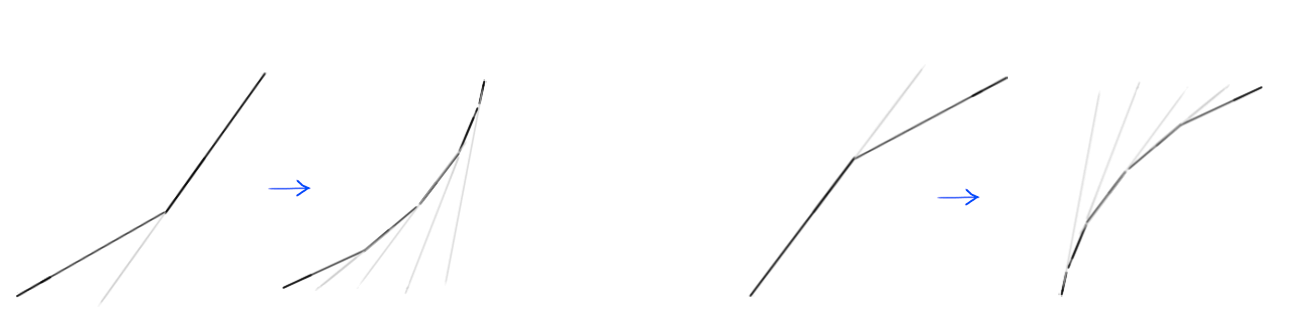
Со всеми этими знаниями понимание кривых движения становится намного проще. Давайте рассмотрим несколько примеров.

Использование кривых движения в анимации пользовательского интерфейса

В следующий раз, когда вам нужно будет анимировать элемент пользовательского интерфейса, в вашем распоряжении будет мощь кривых движения. Будь то выдвижная панель, модальное окно или выпадающее меню, добавление нужного количества анимации и обеспечение плавного и естественного вида значительно повысит качество вашего пользовательского интерфейса. Это сделает пользовательский интерфейс просто приятным . Возьмите выдвижное меню ниже:

При нажатии на меню гамбургера открывается меню слева, но анимация кажется блочной. Строка 51 CSS показывает, что для анимации transition-timing-function установлена ​​на linear . Мы можем улучшить это. Давайте перейдем к кубическому безье и создадим пользовательскую функцию синхронизации.

Если вы читаете это, можно с уверенностью предположить, что вы дизайнер, или разработчик, или и то, и другое, и, следовательно, знакомы с кубическими кривыми Безье; есть большая вероятность, что вы столкнулись с ними хотя бы один раз. Кривые Безье — это чудо. Они используются в основном в компьютерной графике для рисования фигур и используются в таких инструментах, как Sketch и Adobe Illustrator, для рисования векторной графики. Причина популярности кубических кривых Безье заключается в простоте их использования: просто измените положение четырех разных точек и создайте нужную вам кривую.

Поскольку мы всегда знаем начальное и конечное состояния анимированного объекта, мы можем зафиксировать две точки. Остаются только две точки, позиции которых мы должны изменить. Две фиксированные точки называются опорными, а две оставшиеся — контрольными.

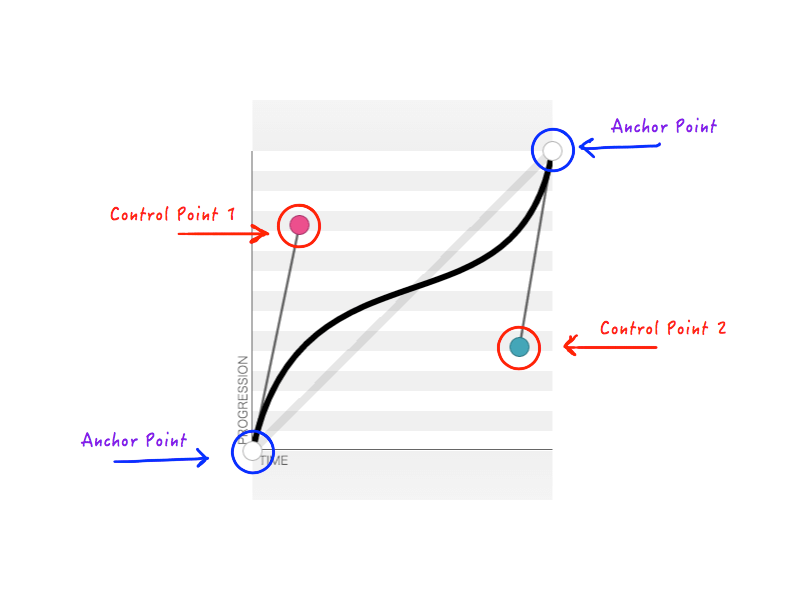
Как вы помните, cubic-bezier принимает четыре числа ( n1, n2, n3, n4 ) при создании пользовательской transition-timing-function . Эти четыре числа представляют собой не что иное, как положения двух контрольных точек: n1, n2 представляют собой координаты x и y первой контрольной точки, а n3, n4 представляют собой координаты второй контрольной точки. Поскольку изменение положения контрольных точек изменит форму кривой и, следовательно, нашу анимацию в целом, результат будет таким же, когда будут изменены любые или все n1, n2, n3, n4 . Например, на рисунке ниже представлен cubic-bezier(.14, .78, .89, .35) :

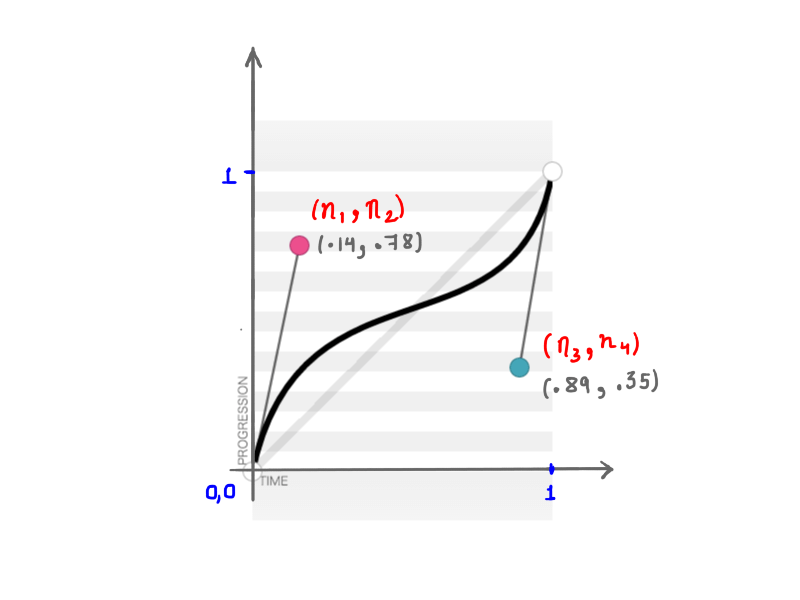
Математика этих, казалось бы, простых кривых завораживает.

Ладно, ладно, давайте вернемся к тому, к чему мы шли с Cubase-bezier: к созданию пользовательской transition-timing-function . Мне нужна анимация, в которой меню появляется очень быстро, а затем изящно замедляется и заканчивается:

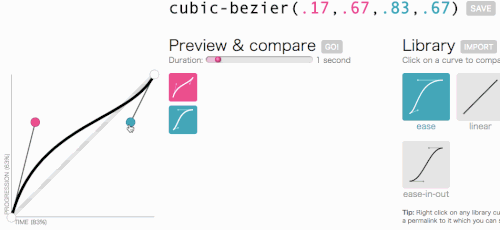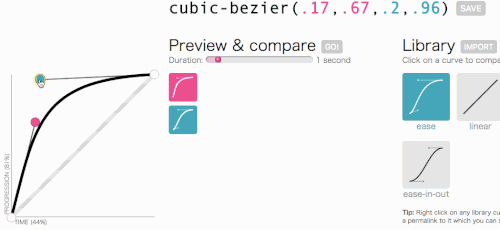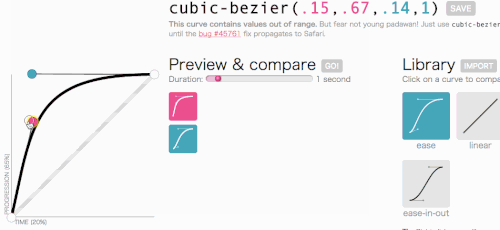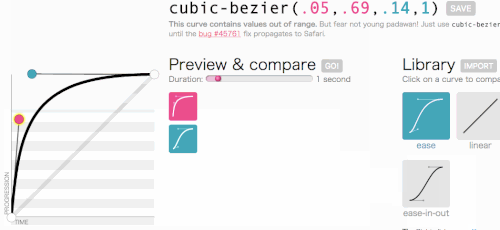
Это выглядит хорошо. Анимация будет начинаться быстро, а затем замедляться, а не двигаться с постоянной скоростью на всем протяжении. Я просто скопирую cubic-bezier(.05, .69, .14, 1) из верхней части страницы и заменю им linear .

Увидеть разницу? Вторая итерация кажется гораздо более естественной и привлекательной. Представьте, если бы каждая анимация в вашем пользовательском интерфейсе следовала естественной временной функции. Насколько это было бы здорово?

Как мы видели, кривые движения вовсе не сложны. Их очень легко понять и использовать. С ними вы можете вывести свой пользовательский интерфейс на новый уровень.

Надеюсь, вы узнали, как работают кривые движения. Если вы прошли через множество проб и ошибок, чтобы заставить кривые движения работать так, как вы хотите, или если вы вообще их не использовали, теперь вам должно быть удобно сгибать их по своему желанию и создавать красивые анимации. Потому что, в конце концов, анимация имеет значение.