Производная цепного правила в машинном обучении: объяснение

Машинное обучение превратилось в одну из самых обсуждаемых и исследуемых областей в последние годы, и на это есть веские причины. Каждый день открываются новые модели и приложения машинного обучения, и исследователи по всему миру работают над созданием следующего большого проекта.

В результате среди профессионалов из разных областей возрос интерес к машинному обучению и участию в этой продолжающейся революции. Если вы один из таких энтузиастов машинного обучения, которые хотят сделать свои первые шаги, позвольте сказать вам, что это начинается с понимания основ математики и статистики прежде всего.

Одной из таких важных тем в математике, которая очень важна для машинного обучения, являются производные. Из вашего базового понимания исчисления вы помните, что производная любой функции — это мгновенная скорость изменения этой функции. В этом блоге мы углубимся в деривативы и изучим цепное правило. Мы увидим, как изменится выход конкретной функции, когда мы изменим некоторые независимые переменные в уравнении. Зная производные цепных правил, вы сможете работать над дифференцированием более сложных функций, с которыми вы наверняка столкнетесь в машинном обучении.

Получите онлайн- сертификаты по машинному обучению в ведущих университетах мира — магистерские программы, программы последипломного образования для руководителей и продвинутые программы сертификации в области машинного обучения и искусственного интеллекта, чтобы ускорить свою карьеру.

Понимание производной цепного правила

Цепное правило — это, по сути, математическая формула, которая помогает вычислить производную сложной функции. Составная функция — это функция, состоящая из двух или более функций. Итак, если f и g — две функции, то цепное правило поможет нам найти производную составных функций, таких как туман или движение f.

Учитывая туман составной функции , вот как будет выглядеть производная цепного правила:

Вышеупомянутое правило также может быть записано как:

Где функция F представляет собой композицию f и g в виде f(g(x)).

Теперь предположим, что у нас есть три переменные, так что третья переменная (z) зависит от второй переменной (y), которая, в свою очередь, зависит от первой переменной (x). В этом случае производная цепного правила будет выглядеть примерно так:

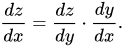С точки зрения глубокого обучения, эта формула также регулярно используется для решения проблем обратного распространения ошибки. Теперь, поскольку мы упомянули, что z зависит от y, а y от x, мы можем написать z = f(y) и y = g(x). Эта замена изменит наше дифференциальное уравнение следующим образом:

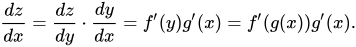Теперь давайте рассмотрим несколько примеров производных цепных правил, чтобы лучше понять их математику.

Примеры и приложения производной цепного правила

Давайте возьмем известный пример из Википедии, чтобы лучше понять производную цепного правила. Предположим, вы совершаете свободное падение с неба. Атмосферное давление, с которым вы столкнетесь во время падения, будет постоянно меняться. Вот график, на котором показано изменение атмосферного давления в зависимости от высоты над уровнем моря:

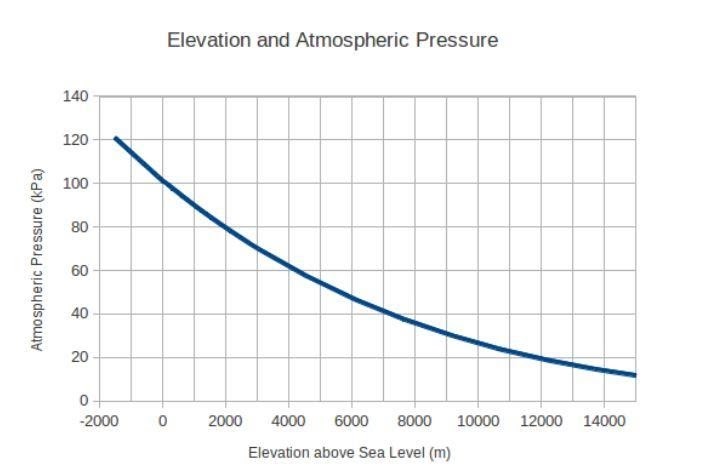
Предположим, ваше падение началось на высоте 4000 метров над уровнем моря. Изначально ваша скорость была равна нулю, а значение ускорения из-за силы тяжести составляло 9,8 метра в секунду в квадрате.

Теперь давайте сравним эту ситуацию с предыдущим методом цепного правила. В этом примере мы будем использовать переменную «t» для времени вместо x.

Тогда переменная y = g(t), которая указывает расстояние, пройденное с начала падения, может быть задана как:

г (т) = 0,5 * 9,8 т ^ 2

А высота от уровня моря может быть задана переменной h, которая будет равна 400-g(t).

Предположим, что на основе модели мы также можем записать функцию атмосферного давления на любой высоте h в виде:

f(h) = 101325 e−0,0001h

Теперь вы можете различать два уравнения на основе их зависимых переменных, чтобы получить следующие результаты:

г'(т) = -9,8т,

Здесь g'(t) указывает значение вашей скорости в любой момент времени t.

f′(h) = −10,1325e−0,0001h

Здесь f′(h) — скорость изменения атмосферного давления по отношению к высоте h. Теперь вопрос в том, можем ли мы объединить эти два уравнения и вывести скорость изменения атмосферного давления в зависимости от времени? Давайте посмотрим, используя цепное правило:

Последнее уравнение, которое мы получили, дает нам скорость изменения атмосферного давления по отношению ко времени, прошедшему с момента падения. С точки зрения машинного обучения, нейронные сети постоянно нуждаются в обновлении веса, связанного с ошибкой нейрона в предсказании. Цепное правило помогает скорректировать эти веса и приблизить модель машинного обучения к правильному результату.

Заключение

Как видите, цепное правило полезно для многих целей. Особенно когда речь идет о машинном обучении или глубоком обучении, цепное правило находит широкое применение для обновления весов нейронов и повышения общей эффективности модели.

Теперь, когда вы знакомы с основами цепного правила, попробуйте решить несколько задач самостоятельно. Найдите несколько составных функций и попытайтесь найти их производные. Чем больше вы будете практиковаться, тем яснее будут становиться ваши концепции и тем проще вам будет обучать свои модели машинного обучения! Тем не менее, если вы энтузиаст машинного обучения, но изо всех сил пытаетесь сделать свои первые шаги в этой области, upGrad поддержит вас!

Наша программа Executive PG в области машинного обучения и искусственного интеллекта предлагается в сотрудничестве с IIIT-Bangalore и дает вам выбор из шести отраслевых специализаций. Курс начинается с уровня земли и ведет вас к вершине, предоставляя вам поддержку один на один от отраслевых экспертов, сильную группу сверстников и всестороннюю поддержку карьеры.