Бинарное дерево против бинарного дерева поиска: разница между бинарным деревом и бинарным деревом поиска
Опубликовано: 2021-01-21Оглавление
Введение
Сортировка — это процесс упорядочивания данных в систематическом порядке, чтобы их можно было проанализировать более эффективно. Процесс идентификации конкретной записи называется поиском. Если данные правильно отсортированы в определенном порядке, поиск становится простой и эффективной задачей. В этой статье рассматривается одна из самых важных нелинейных структур данных — деревья.
Деревья в основном используются для представления данных путем демонстрации иерархических отношений между элементами. Например, оглавление, генеалогическое древо. Технически дерево можно определить как конечное множество «T», состоящее из одного или нескольких узлов, так что узел назначается корнем дерева, а остальные узлы делятся на n>=0 непересекающихся множеств T1, T2, T3, Т4…. Tn и называются поддеревьями или дочерними элементами этого корневого узла.
Что такое бинарное дерево?
Двоичное дерево — это нелинейная структура данных, в которой узел может иметь 0, 1 или 2 узла. Каждый узел в бинарном дереве называется либо родительским узлом, либо дочерним узлом. Самый верхний узел бинарного дерева называется корневым узлом. Каждый родительский узел может иметь не более двух дочерних узлов, которые являются левым дочерним узлом и правым дочерним узлом.
У узла в бинарном дереве есть три поля:
- Элемент данных — в нем хранится значение данных, которое должно быть сохранено узлом.
- Указатель на левый дочерний узел — хранит ссылку (или адрес) на левый дочерний узел.
- Указатель на правый дочерний элемент — хранит ссылку на правый дочерний узел.
Таким образом, несколько узлов объединяются для построения двоичного дерева.
Двоичное дерево может быть представлено как:
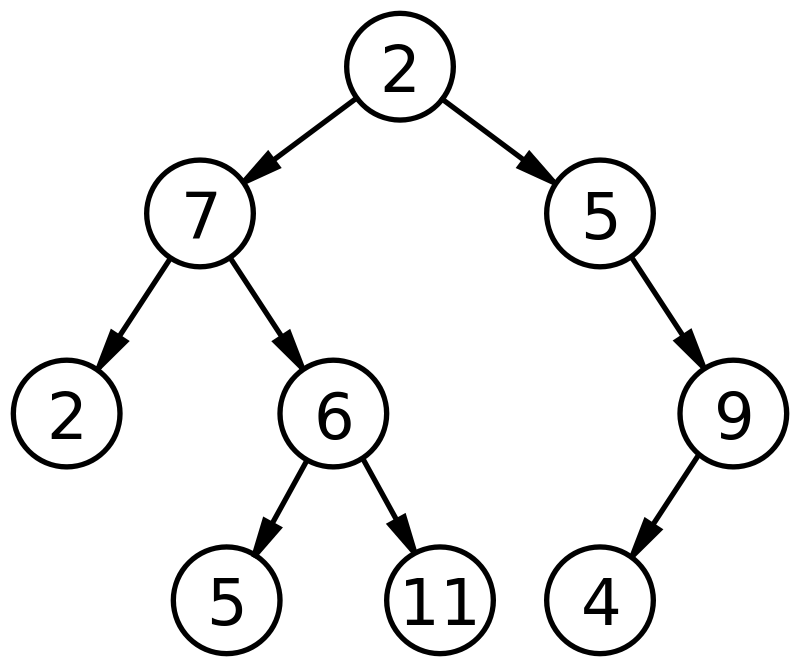
Источник
На приведенном выше рисунке корневой узел 2 имеет двух дочерних элементов (или дочерних узлов), 7 и 5. 7 называется левым дочерним узлом, а 5 называется правым дочерним узлом. Таким образом, каждый из дочерних узлов действует как родительский узел для нескольких других узлов и вместе представляет собой двоичное дерево.
Отъезд: Типы бинарного дерева
Терминология, используемая в двоичном дереве
Узел : базовое представление точки завершения в дереве.
Корневой узел : самый верхний узел двоичного дерева.
Родительский узел : если узел соединен с другим узлом через ребра, он называется родительским узлом. В бинарном дереве родительский узел может иметь максимум 2 дочерних узла.
Дочерний узел : если у узла есть предшественник, он называется дочерним узлом.
Листовой узел : узел, не имеющий дочерних узлов, называется листовым узлом.
Глубина узла : это расстояние от корневого узла до того конкретного узла, глубину которого необходимо измерить.
Высота дерева : это самое длинное расстояние от корневого узла до конечного узла.
Это несколько основных терминов бинарного дерева. С этим базовым пониманием двоичного дерева давайте перейдем к усовершенствованию двоичного дерева, известному как двоичное дерево поиска.
Читайте также: Алгоритм бинарного поиска: функция, преимущества, временная и пространственная сложность
Что такое бинарное дерево поиска
Как следует из названия, двоичное дерево поиска или BST — это дерево, которое используется для сортировки, извлечения и поиска данных. Это также тип нелинейной структуры данных, в которой узлы расположены в определенном порядке. Следовательно, его также называют « упорядоченным двоичным деревом ». Он имеет следующие свойства:
- В левом поддереве узла есть узлы, которые меньше ключа этого узла.
- В правом поддереве узла есть узлы, которые только больше, чем ключ этого узла.
- Каждый узел имеет разные ключи, и дубликаты не допускаются в двоичном дереве поиска.
- Левое и правое поддеревья также должны быть бинарными деревьями поиска.
Давайте визуализируем эту концепцию, чтобы получить четкое представление о бинарных деревьях поиска.
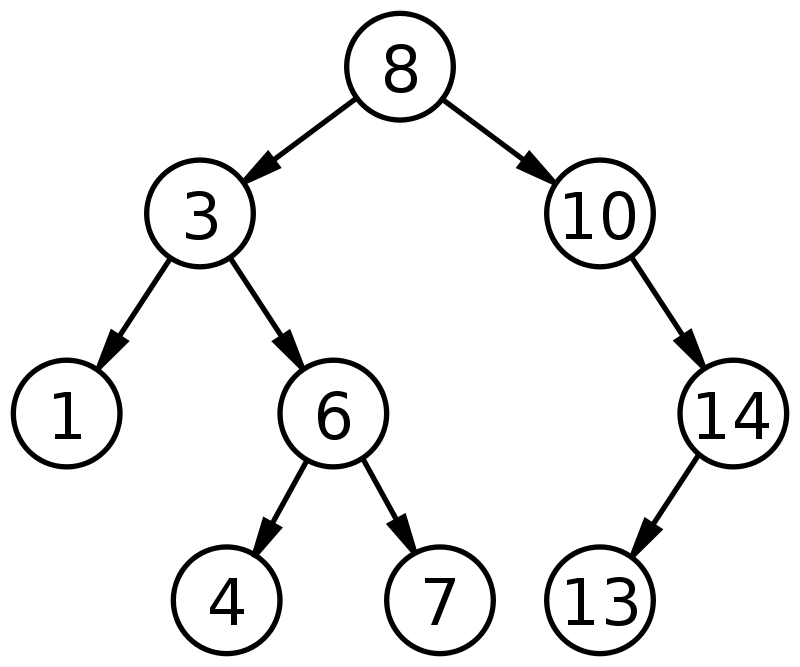
Источник
На приведенном выше рисунке мы видим, что значение корневого узла равно 8. При дальнейшем рассмотрении видно, что все значения в левом поддереве меньше значения корневого узла, а все значения в правом поддереве имеют значения, которые больше, чем корневой узел. Кроме того, следует отметить, что каждое значение в двоичном дереве поиска уникально и не имеет дубликатов. Таким образом, указанные выше свойства бинарного дерева поиска проверяются.
В еще одном примере мы видим, что хотя левое и правое поддеревья являются бинарными деревьями поиска с уникальными значениями по всему дереву. Значение в листовом узле в левом поддереве равно 12, что больше, чем значение корневого узла, равное 12. Таким образом, это не удовлетворяет свойству BST и, следовательно, это не двоичное дерево поиска.
Операция поиска в BST –
Рассмотрим двоичное дерево поиска со значениями, приведенными ниже. Давайте разберемся, как выполняется операция поиска, чтобы получить 9 из двоичного дерева поиска.

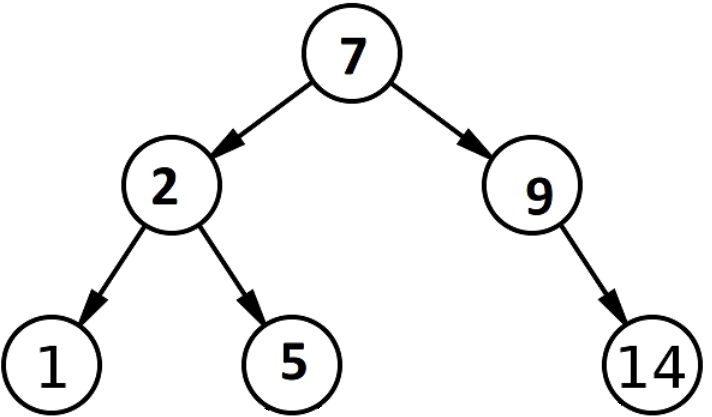
Источник
Чтобы выполнить бинарный поиск, мы сначала упорядочим все целые числа в отсортированном массиве. Это называется пространством поиска. Это пространство поиска должно состоять из двух указателей, называемых начальным и конечным указателями. Массив приведенного выше бинарного дерева поиска представлен в виде:
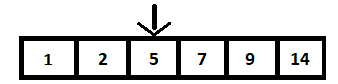
Первый шаг — вычислить среднее значение массива и сравнить его с искомым значением, в нашем случае 9. Это делается путем вычисления n/2, где n — общее количество элементов в массиве (BST), равное 6. Таким образом, 3- й элемент — это средний элемент, равный 5.
Теперь, когда средний элемент сравнивается с 9 и так как он не равен (больше), операция поиска будет выполняться на правом массиве. Таким образом, операция поиска сокращается вдвое, как показано ниже:
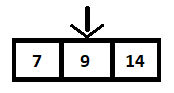
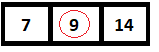
На следующем шаге средний элемент вычисляется и оказывается равным 9, что соответствует нашему элементу для поиска.
Бинарное дерево против бинарного дерева поиска –
Теперь, когда у нас есть общее представление как о бинарном дереве, так и о бинарных деревьях поиска, давайте быстро суммируем некоторые различия между ними обоими.
| Основание для сравнения | Бинарное дерево | Бинарное дерево поиска |
| Определение | Двоичное дерево — это нелинейная структура данных, в которой узел может иметь 0, 1 или 2 узла. По отдельности каждый узел состоит из левого указателя, правого указателя и элемента данных. | Двоичное дерево поиска — это организованное двоичное дерево со структурированной организацией узлов. Каждое поддерево также должно иметь эту конкретную структуру. |
| Структура | В дереве нет необходимой организационной структуры узлов. | Значения левого поддерева определенного узла должны быть меньше этого узла, а значения правого поддерева должны быть больше. |
| Выполненные операции | Операции, которые могут быть выполнены, это удаление, вставка и обход | Поскольку это отсортированные двоичные деревья, они используются для быстрого и эффективного двоичного поиска, вставки и удаления. |
| Типы | Есть несколько типов. Наиболее распространенными являются полное двоичное дерево, полное двоичное дерево, расширенное двоичное дерево. | Самые популярные из них — AVL Trees, Splay Trees, Tango Trees, T-Trees. |
Заключение
Таким образом, мы делаем вывод, что, хотя и двоичное дерево, и двоичное дерево поиска имеют общую иерархическую структуру с набором узлов, они имеют несколько различий в своем применении. Двоичное дерево — это базовая структура с простым правилом, согласно которому ни один родитель не должен иметь более двух дочерних элементов, тогда как двоичное дерево поиска — это вариант двоичного дерева, следующий определенному порядку, в котором должны быть организованы узлы.
Если вам интересно узнать о бинарном дереве и бинарном дереве поиска, ознакомьтесь с дипломом PG IIIT-B и upGrad в области науки о данных, который создан для работающих профессионалов и предлагает более 10 тематических исследований и проектов, практические практические семинары, наставничество в отрасли. экспертов, общение один на один с отраслевыми наставниками, более 400 часов обучения и помощь в трудоустройстве в ведущих фирмах.
Изучайте онлайн- курсы по науке о данных в лучших университетах мира. Участвуйте в программах Executive PG, Advanced Certificate Programs или Master Programs, чтобы ускорить свою карьеру.
Как мы можем пройти по двоичному дереву поиска?
В отличие от линейных структур данных, таких как массивы, связанные списки, стеки и очереди, где мы можем перемещаться по структуре данных только одним способом, двоичное дерево поиска дает нам возможность перемещаться по ней несколькими способами. Наиболее популярные обходы дерева следующие: при неупорядоченном обходе мы сначала обходим левый узел дерева, затем корневой узел дерева и, наконец, правый узел дерева. Мы следуем тому же принципу и во всех поддеревьях. При обходе в прямом порядке мы сначала обходим корневой узел дерева, а затем левый и правый узлы соответственно. Мы следуем тому же принципу и во всех поддеревьях. При обходе в обратном порядке мы сначала обходим левый и правый узлы дерева соответственно и, наконец, корневой узел дерева. Мы следуем тому же принципу и во всех поддеревьях.
Каковы преимущества и недостатки BST?
Ниже приведены преимущества и недостатки двоичного дерева поиска. Преимущества: такие операции, как вставка, удаление и поиск, могут выполняться за время O (log n), где n — количество узлов. Все элементы в BST отсортированы, поэтому мы можем легко пройти через BST, просто используя неупорядоченный обход. BST можно эффективно использовать для разработки распределителей памяти, чтобы ускорить процесс поиска блоков памяти. Самым большим недостатком двоичного дерева поиска является то, что мы всегда должны использовать сбалансированный BST, такой как AVL и красно-черное дерево, потому что, если мы не используем сбалансированный BST, наши операции с деревом не будут выполняться за логарифмическое время.
Отличие полного бинарного дерева от полного бинарного дерева.
Полное бинарное дерево — это бинарное дерево, в котором все узлы имеют дочерние узлы от 0 до 2. Другими словами, бинарное дерево, в котором все узлы имеют по крайней мере 2 дочерних узла, кроме листовых узлов, называется полным бинарным деревом. С другой стороны, полное бинарное дерево — это бинарное дерево, в котором каждый узел полностью заполнен (ровно два дочерних узла), а конечные узлы расположены как можно левее.
