Теорема Байеса в машинном обучении: введение, применение и пример
Опубликовано: 2021-02-04Оглавление
Введение: что такое теорема Байеса?
Теорема Байеса названа в честь английского математика Томаса Байеса, который много работал в области теории принятия решений, области математики, связанной с вероятностями. Теорема Байеса также широко используется в машинном обучении, где она представляет собой простой и эффективный способ прогнозирования классов с точностью и достоверностью. Байесовский метод расчета условных вероятностей используется в приложениях машинного обучения, которые включают задачи классификации.
Упрощенная версия теоремы Байеса, известная как наивная байесовская классификация, используется для сокращения времени и затрат на вычисления. В этой статье мы познакомим вас с этими концепциями и обсудим применение теоремы Байеса в машинном обучении.
Присоединяйтесь к онлайн- курсу по машинному обучению в ведущих университетах мира — магистерским программам, программам последипломного образования для руководителей и продвинутой сертификационной программе в области машинного обучения и искусственного интеллекта, чтобы ускорить свою карьеру.
Зачем использовать теорему Байеса в машинном обучении?
Теорема Байеса — это метод определения условных вероятностей, то есть вероятности наступления одного события при условии, что другое событие уже произошло. Поскольку условная вероятность включает дополнительные условия — другими словами, больше данных — она может способствовать получению более точных результатов.
Таким образом, условные вероятности необходимы для определения точных прогнозов и вероятностей в машинном обучении. Учитывая, что эта область становится все более распространенной в различных областях, важно понимать роль алгоритмов и методов, таких как теорема Байеса, в машинном обучении.
Прежде чем мы перейдем к самой теореме, давайте разберемся с некоторыми терминами на примере. Скажем, менеджер книжного магазина располагает информацией о возрасте и доходах своих клиентов. Он хочет знать, как распределяются продажи книг по трем возрастным классам покупателей: молодежь (18–35 лет), средний возраст (35–60 лет) и пожилые люди (60+).

Назовем наши данные X. В байесовской терминологии X называется свидетельством. У нас есть некоторая гипотеза H, где у нас есть некоторое X, принадлежащее некоторому классу C.
Наша цель — определить условную вероятность нашей гипотезы H при заданном X, т. е. P(H | X).
Проще говоря, определяя P(H | X), мы получаем вероятность принадлежности X к классу C при заданном X. X имеет атрибуты возраста и дохода — скажем, например, 26 лет с доходом 2000 долларов. H — наша гипотеза о том, что покупатель купит книгу.
Обратите особое внимание на следующие четыре термина:
- Свидетельство . Как обсуждалось ранее, P(X) известно как свидетельство. Это просто вероятность того, что в этом случае покупателю будет 26 лет, и он заработает 2000 долларов.
- Априорная вероятность — P(H), известная как априорная вероятность, — это простая вероятность нашей гипотезы, а именно того, что покупатель купит книгу. Эта вероятность не будет обеспечена какими-либо дополнительными входными данными в зависимости от возраста и дохода. Поскольку расчет выполняется с меньшим количеством информации, результат менее точен.
- Апостериорная вероятность — P(H | X) известна как апостериорная вероятность. Здесь P(H | X) — это вероятность того, что покупатель купит книгу (H) при условии X (что ему 26 лет и он зарабатывает 2000 долларов).
- Вероятность — P(X | H) — вероятность вероятности. В этом случае, учитывая, что мы знаем, что покупатель купит книгу, вероятность правдоподобия — это вероятность того, что покупателю 26 лет и его доход составляет 2000 долларов.
Учитывая это, теорема Байеса утверждает:
P(H | X) = [P(X | H) * P(H)] / P(X)
Обратите внимание на появление в теореме четырех приведенных выше терминов: апостериорная вероятность, вероятность правдоподобия, априорная вероятность и свидетельство.
Читайте: Объяснение наивного Байеса
Как применить теорему Байеса в машинном обучении
Наивный байесовский классификатор, упрощенная версия теоремы Байеса, используется в качестве алгоритма классификации для классификации данных по различным классам с точностью и скоростью.
Давайте посмотрим, как можно применить наивный байесовский классификатор в качестве алгоритма классификации.
- Рассмотрим общий пример: X — вектор, состоящий из n атрибутов, то есть X = {x1, x2, x3, …, xn}.
- Скажем, у нас есть m классов {C1, C2, …, Cm}. Наш классификатор должен будет предсказать, что X принадлежит к определенному классу. Класс, обеспечивающий наибольшую апостериорную вероятность, будет выбран как лучший класс. Таким образом, математически классификатор будет предсказывать класс Ci тогда и только тогда, когда P(Ci | X) > P(Cj | X). Применение теоремы Байеса:
P(Ci | X) = [P(X | Ci) * P(Ci)] / P(X)
- P(X), будучи независимым от условий, постоянен для каждого класса. Таким образом, чтобы максимизировать P(Ci | X), мы должны максимизировать [P(X | Ci) * P(Ci)]. Учитывая, что все классы равновероятны, мы имеем P(C1) = P(C2) = P(C3) … = P(Cn). Таким образом, в конечном итоге нам нужно максимизировать только P(X | Ci).
- Поскольку типичный большой набор данных, вероятно, будет иметь несколько атрибутов, выполнение операции P(X | Ci) для каждого атрибута требует значительных вычислительных ресурсов. Именно здесь вступает в действие условно-классовая независимость, которая упрощает задачу и снижает затраты на вычисления. Под классово-условной независимостью мы подразумеваем, что мы считаем значения атрибута независимыми друг от друга условно. Это наивная байесовская классификация.
P(Xi | C) = P(x1 | C) * P(x2 | C) *… * P(xn | C)
Теперь легко вычислить меньшие вероятности. Здесь важно отметить одну важную вещь: поскольку xk принадлежит каждому атрибуту, нам также необходимо проверить, является ли атрибут, с которым мы имеем дело, категориальным или непрерывным .
- Если у нас есть категориальный атрибут, все проще. Мы можем просто подсчитать количество экземпляров класса Ci, состоящих из значения xk для атрибута k, а затем разделить его на количество экземпляров класса Ci.
- Если у нас есть непрерывный атрибут, учитывая, что у нас есть функция нормального распределения, мы применяем следующую формулу со средним значением ? и стандартное отклонение ?:
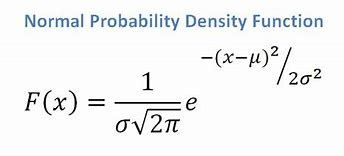

Источник
В конечном итоге мы получим P(x | Ci) = F(xk, ?k, ?k).
- Теперь у нас есть все значения, необходимые для использования теоремы Байеса для каждого класса Ci. Наш прогнозируемый класс будет классом, достигающим наибольшей вероятности P(X | Ci) * P(Ci).
Пример: Предиктивная классификация покупателей книжного магазина
У нас есть следующий набор данных из книжного магазина:
| Возраст | Доход | Ученик | Кредит_Рейтинг | Buys_Book |
| Молодость | Высоко | Нет | Справедливый | Нет |
| Молодость | Высоко | Нет | Превосходно | Нет |
| Среднего возраста | Высоко | Нет | Справедливый | да |
| Старший | Середина | Нет | Справедливый | да |
| Старший | Низкий | да | Справедливый | да |
| Старший | Низкий | да | Превосходно | Нет |
| Среднего возраста | Низкий | да | Превосходно | да |
| Молодость | Середина | Нет | Справедливый | Нет |
| Молодость | Низкий | да | Справедливый | да |
| Старший | Середина | да | Справедливый | да |
| Молодость | Середина | да | Превосходно | да |
| Среднего возраста | Середина | Нет | Превосходно | да |
| Среднего возраста | Высоко | да | Справедливый | да |
| Старший | Середина | Нет | Превосходно | Нет |
У нас есть такие атрибуты, как возраст, доход, студент и кредитный рейтинг. Наш класс, buys_book, имеет два результата: Да или Нет.
Наша цель состоит в том, чтобы классифицировать на основе следующих признаков:
X = {возраст = молодежь, студент = да, доход = средний, кредитный_рейтинг = удовлетворительный}.
Как мы показали ранее, чтобы максимизировать P(Ci | X), нам нужно максимизировать [P(X | Ci) * P(Ci)] для i = 1 и i = 2.
Следовательно, P(buys_book = yes) = 9/14 = 0,643.
P(buys_book = нет) = 5/14 = 0,357
P(возраст = молодость | покупка_книги = да) = 2/9 = 0,222
P(возраст = молодость | покупка_книги = нет) = 3/5 = 0,600
P(доход = средний | книга_покупок = да) = 4/9 = 0,444
P(доход = средний | книга_покупок = нет) = 2/5 = 0,400
P(студент = да | покупает_книгу = да) = 6/9 = 0,667
P(студент = да | покупает_книгу = нет) = 1/5 = 0,200
P(кредит_рейтинг = справедливо | книга_покупок = да) = 6/9 = 0,667
P(кредит_рейтинг = справедливо | книга_покупок = нет) = 2/5 = 0,400
Используя вычисленные выше вероятности, имеем
P(X | книга_покупок = да) = 0,222 х 0,444 х 0,667 х 0,667 = 0,044
По аналогии,
P(X | buys_book = нет) = 0,600 х 0,400 х 0,200 х 0,400 = 0,019
Какой класс Ci обеспечивает максимальное значение P(X|Ci)*P(Ci)? Мы вычисляем:
P(X | покупка_книги = да) * P(покупки_книги = да) = 0,044 x 0,643 = 0,028
P(X | покупка_книги = нет) * P(покупки_книги = нет) = 0,019 x 0,357 = 0,007

Сравнивая два вышеупомянутых, поскольку 0,028> 0,007, наивный байесовский классификатор предсказывает, что покупатель с вышеупомянутыми атрибутами купит книгу.
Оформить заказ: идеи и темы проекта машинного обучения
Является ли байесовский классификатор хорошим методом?
Алгоритмы, основанные на теореме Байеса в машинном обучении, дают результаты, сравнимые с другими алгоритмами, а байесовские классификаторы обычно считаются простыми высокоточными методами. Однако следует помнить, что байесовские классификаторы особенно подходят там, где справедливо предположение об условной независимости классов, а не во всех случаях. Еще одна практическая проблема заключается в том, что сбор всех вероятностных данных не всегда может быть осуществим.
Заключение
Теорема Байеса имеет множество приложений в машинном обучении, особенно в задачах, основанных на классификации. Применение этого семейства алгоритмов в машинном обучении предполагает знакомство с такими терминами, как априорная вероятность и апостериорная вероятность. В этой статье мы обсудили основы теоремы Байеса, ее использование в задачах машинного обучения и рассмотрели пример классификации.
Поскольку теорема Байеса является важной частью алгоритмов на основе классификации в машинном обучении, вы можете узнать больше о программе расширенных сертификатов upGrad в области машинного обучения и НЛП . Этот курс был разработан с учетом различных типов студентов, заинтересованных в машинном обучении, предлагая индивидуальное наставничество и многое другое.
Почему мы используем теорему Байеса в машинном обучении?
Теорема Байеса — это метод расчета условных вероятностей или вероятности наступления одного события, если ранее произошло другое. Условная вероятность может привести к более точным результатам за счет включения дополнительных условий — другими словами, большего количества данных. Для получения правильных оценок и вероятностей в машинном обучении требуются условные вероятности. Учитывая растущую распространенность этой области в широком диапазоне областей, важно понимать важность алгоритмов и подходов, таких как теорема Байеса, в машинном обучении.
Является ли байесовский классификатор хорошим выбором?
В машинном обучении алгоритмы, основанные на теореме Байеса, дают результаты, сравнимые с результатами других методов, а байесовские классификаторы широко считаются простыми высокоточными подходами. Однако важно помнить, что байесовские классификаторы лучше всего использовать, когда верно условие условной независимости классов, а не во всех обстоятельствах. Другое соображение состоит в том, что получение всех данных о вероятности не всегда возможно.
Как можно применить теорему Байеса на практике?
Теорема Байеса вычисляет вероятность возникновения на основе новых данных, которые связаны или могут быть связаны с ним. Этот метод также можно использовать, чтобы увидеть, как гипотетическая новая информация влияет на вероятность события, если предположить, что новая информация верна. Возьмем, к примеру, одну карту, выбранную из колоды из 52 карт. Вероятность того, что карта станет королем, равна 4, разделенному на 52, или 1/13, или примерно 7,69 процента. Имейте в виду, что в колоде четыре короля. Допустим, выяснилось, что выбранная карта является лицевой. Поскольку в колоде 12 лицевых карт, вероятность того, что выбранная карта является королем, равна 4, разделенным на 12, или примерно 33,3 процента.
