Теорема Байеса, объясненная на примере - полное руководство

Введение

Что такое теорема Байеса?

Теорема Байеса используется для расчета условной вероятности там, где интуиция часто подводит. Хотя эта теорема широко используется в теории вероятностей, она применяется и в области машинного обучения. Его использование в машинном обучении включает в себя подгонку модели к обучающему набору данных и разработку моделей классификации.

Что такое условная вероятность?

Условная вероятность обычно определяется как вероятность одного события при наступлении другого события.

• Если А и В — два события, то условную вероятность можно обозначить как Р(А при данном В) или Р(А|В).
• Условная вероятность может быть рассчитана из совместной вероятности (A | B) = P(A, B) / P(B)

• Условная вероятность несимметрична; Например, P(A | B) != P(B | A)

Другие способы вычисления условной вероятности включают использование другой условной вероятности, т.е.

Р(А|В) = Р(В|А) * Р(А) / Р(В)

Также используется реверс

Р(В|А) = Р(А|В) * Р(В) / Р(А)

Этот способ расчета полезен, когда сложно вычислить совместную вероятность. В противном случае, когда доступна обратная условная вероятность, расчет с ее помощью становится легким.

Этот альтернативный расчет условной вероятности называется правилом Байеса или теоремой Байеса. Он назван в честь человека, впервые описавшего его, «преподобного Томаса Байеса».

Формула теоремы Байеса

Теорема Байеса — это способ вычисления условной вероятности, когда совместная вероятность недоступна. Иногда к знаменателю нельзя получить прямой доступ. В таких случаях альтернативный способ расчета выглядит следующим образом:

P(B) = P(B|A) * P(A) + P(B|не A) * P(не A)

Это формулировка теоремы Байеса, которая показывает альтернативный расчет P(B).

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|не A) * P(не A)

Вышеприведенная формула может быть описана со скобками вокруг знаменателя

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|не A) * P(не A))

Кроме того, если у нас есть P (A), то P (не A) можно рассчитать как

Р(не А) = 1 – Р(А)

Точно так же, если у нас есть P (не B | не A), то P (B | не A) можно рассчитать как

P(B|не A) = 1 – P(не B|не A)

Теорема Байеса об условной вероятности

Теорема Байеса состоит из нескольких терминов, имена которых даны в зависимости от контекста ее применения в уравнении.

Апостериорная вероятность относится к результату P(A|B), а априорная вероятность относится к P(A).

• P(A|B): апостериорная вероятность.
• P(A): Априорная вероятность.

Точно так же P (B | A) и P (B) называются вероятностью и доказательством.

• P(B|A): Вероятность.
• П(Б): Доказательства.

Следовательно, теорему Байеса об условной вероятности можно переформулировать так:

Апостериорная = вероятность * априорная/доказательство

Если нам нужно вычислить вероятность пожара при наличии дыма, то будет использовано следующее уравнение:

P(огонь|дым) = P(дым|огонь) * P(огонь) / P(дым)

Где P(огонь) — это априор, P(дым|огонь) — это вероятность, а P(дым) — свидетельство.

Иллюстрация теоремы Байеса

Пример теоремы Байеса описан для иллюстрации использования теоремы Байеса в задаче.

Проблема

Имеются три коробки, помеченные буквами A, B и C. Детали ящиков:

• В коробке А 2 красных и 3 черных шара.
• В коробке B находятся 3 красных и 1 черный шар.
• В коробке С 1 красный и 4 черных шара.

Все три ящика идентичны и имеют одинаковую вероятность быть поднятыми. Следовательно, какова вероятность того, что красный шар был взят из ящика А?

Решение

Пусть E обозначает событие взятия красного шара, а A, B и C обозначают взятие шара из соответствующих ящиков. Следовательно, условная вероятность будет равна P(A|E), которую необходимо рассчитать.

Существующие вероятности P(A) = P(B) = P(C) = 1/3, так как все ящики имеют одинаковую вероятность быть выбранными.

P(E|A) = количество красных шаров в коробке A / общее количество шаров в коробке A = 2/5

Точно так же P(E|B) = 3/4 и P(E|C) = 1/5.

Тогда доказательство P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Следовательно, P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296.

Пример теоремы Байеса

Теорема Байеса дает вероятность «события» при заданной информации о «испытаниях».

• Есть разница между «событиями» и «тестами». Например, есть тест на заболевание печени, который отличается от фактического наличия заболевания печени, т.е. события.
• Редкие события могут иметь более высокий уровень ложноположительных результатов.

Пример 1

Какова вероятность заболевания печени у алкоголика?

Здесь «быть алкоголиком» — это «тест» (тип лакмусовой бумажки) на заболевание печени.

• А – это событие, т.е. «у пациента заболевание печени».

Согласно более ранним записям клиники, в ней говорится, что 10% пациентов, поступающих в клинику, страдают заболеваниями печени.

Следовательно, Р(А)=0,10

• Б – лакмусовая бумажка того, что «Пациент – алкоголик».

Более ранние отчеты клиники показали, что 5% пациентов, поступающих в клинику, являются алкоголиками.

Следовательно, P(B)=0,05.

• Также 7% пациентов, у которых диагностировано заболевание печени, являются алкоголиками. Это определяет B|A: вероятность того, что пациент будет алкоголиком, учитывая, что у него есть заболевание печени, составляет 7%.

Как, по формуле теоремы Байеса ,

Р(А|В) = (0,07 * 0,1)/0,05 = 0,14

Таким образом, для больного алкоголиком вероятность заболевания печени составляет 0,14 (14%).

Пример2

• Опасные пожары случаются редко (1%)
• Но дым довольно распространен (10%) из-за барбекю,
• И 90% опасных пожаров вызывают дым

Какова вероятность опасного Огня при наличии Дыма?

Расчет

P(огонь|дым) =P(огонь) P(дым|огонь)/P(дым)

= 1% х 90%/10%

= 9%

Пример 3

Какова вероятность дождя в течение дня? Где Дождь означает дождь в течение дня, а Облако означает облачное утро.

Вероятность дождя с учетом облака записывается как P(Дождь|Облако).

P(Дождь|Облако) = P(Дождь) P(Облако|Дождь)/P(Облако)

P (дождь) - вероятность дождя = 10%

P(Облако|Дождь) — это Вероятность Облаков, учитывая, что Дождь будет = 50%

P(Облако) - Вероятность Облака = 40%

P(Дождь|Облако) = 0,1 x 0,5/0,4 = 0,125

Следовательно, вероятность дождя составляет 12,5%.

Приложения

В реальном мире существует несколько приложений теоремы Байеса. Несколько основных приложений теоремы:

1. Моделирование гипотез

Теорема Байеса находит широкое применение в прикладном машинном обучении и устанавливает связь между данными и моделью. Прикладное машинное обучение использует процесс проверки и анализа различных гипотез на заданном наборе данных.

Для описания взаимосвязи между данными и моделью теорема Байеса предлагает вероятностную модель.

P(h|D) = P(D|h) * P(h) / P(D)

Где,

P(h|D): апостериорная вероятность гипотезы

P(h): Априорная вероятность гипотезы.

Увеличение P(D) уменьшает P(h|D). И наоборот, если P(h) и вероятность наблюдения данных данной гипотезы увеличивается, то вероятность P(h|D) увеличивается.

2. Теорема Байеса для классификации

Метод классификации включает в себя маркировку заданных данных. Его можно определить как вычисление условной вероятности метки класса с учетом выборки данных.

P(класс|данные) = (P(данные|класс) * P(класс)) / P(данные)

Где P (класс | данные) - вероятность класса с учетом предоставленных данных.

Расчет можно проводить для каждого класса. Входным данным может быть присвоен класс, имеющий наибольшую вероятность.

Расчет условной вероятности невозможен в условиях малого числа примеров. Следовательно, прямое применение теоремы Байеса невозможно. Решение модели классификации заключается в упрощенном расчете.

• Наивный байесовский классификатор

Теорема Байеса считает, что входные переменные зависят от других переменных, что усложняет вычисления. Следовательно, предположение снимается, и каждая входная переменная рассматривается как независимая переменная. В результате модель меняется с зависимой на независимую условно-вероятностную модель. В конечном итоге это снижает сложность.

Это упрощение теоремы Байеса называется наивным Байесом. Он широко используется для классификации и прогнозирования моделей.

• Байесовский оптимальный классификатор

Это тип вероятностной модели, которая включает прогнозирование нового примера с учетом набора обучающих данных. Один из примеров оптимального классификатора Байеса: «Какова наиболее вероятная классификация нового экземпляра с учетом обучающих данных?»

Расчет условной вероятности нового экземпляра с учетом обучающих данных можно выполнить с помощью следующего уравнения

P(vj | D) = сумма {h в H} P(vj | hi) * P(hi | D)

Где vj — новый классифицируемый экземпляр,

H - набор гипотез для классификации экземпляра,

привет заданная гипотеза,

P(vj | hi) — апостериорная вероятность для vi данной гипотезы hi, и

P(hi | D) — апостериорная вероятность гипотезы hi при данных D.

3. Использование теоремы Байеса в машинном обучении

Наиболее распространенным применением теоремы Байеса в машинном обучении является разработка задач классификации. Другие приложения, а не классификация, включают оптимизационные и случайные модели.

• Байесовская оптимизация

Всегда сложно найти вход, который приводит к минимальной или максимальной стоимости данной целевой функции. Байесовская оптимизация основана на теореме Байеса и обеспечивает аспект поиска глобальной проблемы оптимизации. Метод включает построение вероятностной модели (суррогатной функции), поиск по функции приобретения и выбор образцов-кандидатов для оценки реальной целевой функции.

В прикладном машинном обучении байесовская оптимизация используется для настройки гиперпараметров хорошо работающей модели.

• Байесовские сети убеждений

Отношения между переменными могут быть определены с помощью вероятностных моделей. Они также используются для расчета вероятностей. Полностью условная вероятностная модель может быть не в состоянии рассчитать вероятности из-за большого объема данных. Наивный Байес упростил подход к расчету. Существует еще один метод, когда модель разрабатывается на основе известной условной зависимости между случайными величинами и условной независимости в других случаях. Байесовская сеть отображает эту зависимость и независимость через модель вероятностного графа с направленными ребрами. Известная условная зависимость отображается в виде направленных ребер, а недостающие соединения представляют собой условные зависимости в модели.

4. Байесовская фильтрация спама

Фильтрация спама — еще одно применение теоремы Байеса. Присутствуют два события:

• Событие A: Сообщение является спамом.
• Тест X: сообщение содержит определенные слова (X)

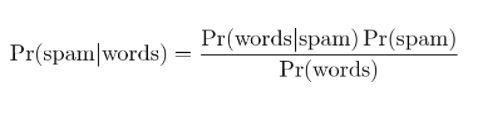
С применением теоремы Байеса можно предсказать, является ли сообщение спамом, учитывая «результаты проверки». Анализ слов в сообщении может рассчитать вероятность того, что оно является спамом. При обучении фильтров повторяющимися сообщениями обновляется факт того, что вероятность наличия определенных слов в сообщении будет спамом.

Применение теоремы Байеса на примере

Производитель катализатора изготавливает прибор для проверки дефектов определенного электрокатализатора (ЭК). Производитель катализатора утверждает, что тест надежен на 97 %, если ЭК неисправен, и на 99 %, если он безупречен. Однако можно ожидать, что 4% указанных ЭК будут бракованными при доставке. Правило Байеса применяется для определения истинной надежности устройства. Базовые наборы событий:

A : EC неисправен; A': ЕС безупречен; B: ЭК проверен на наличие дефектов; B': EC проверен на безупречность.

Вероятность была бы

B / A: EC (известно) дефектный и проверенный дефектный, P (B / A) = 0,97,

B'/A: EC (известно) дефектный, но протестирован безупречно, P(B'/A)=1-P(B/A)=0,03,

B/A': EC (известно) дефектный, но протестированный дефектный, P(B/A') = 1- P(B'/A')=0,01

B'/A: = EC (известно) безупречен и безупречен при испытаниях P(B'/A') = 0,99

Вероятности, рассчитанные по теореме Байеса:

Вероятность расчета показывает, что существует высокая вероятность отбраковки безупречных ЭК (около 20 %) и низкая вероятность выявления дефектных ЭК (около 80 %).

Заключение

Одной из наиболее поразительных особенностей теоремы Байеса является то, что из нескольких отношений вероятностей можно получить огромное количество информации. С помощью средств вероятности вероятность предшествующего события может быть преобразована в апостериорную вероятность. Подходы теоремы Байеса могут применяться в областях статистики, эпистемологии и индуктивной логики.

Если вам интересно узнать больше о теореме Байеса, искусственном интеллекте и машинном обучении, ознакомьтесь с программой IIIT-B & upGrad Executive PG по машинному обучению и искусственному интеллекту, которая предназначена для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 кейсов. исследования и задания, статус выпускника IIIT-B, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.