Ce este Decision Tree în Data Mining? Tipuri, exemple din lumea reală și aplicații

Introducere în Data Mining

Datele sunt adesea prezente ca date brute care trebuie procesate eficient pentru a le converti în informații utile. Predicția rezultatelor se bazează adesea pe procesul de găsire a modelelor, anomaliilor sau corelațiilor în cadrul datelor. Procesul a fost numit „descoperirea cunoștințelor în baze de date”.

Abia în anii 1990 a fost inventat termenul „mining de date”. Miningul de date a fost fondat pe trei discipline: statistică, inteligență artificială și învățare automată. Exploatarea automată a datelor a schimbat procesul de analiză de la o abordare plictisitoare la una mai rapidă. Exploatarea datelor permite utilizatorului

• • Eliminați toate datele zgomotoase și haotice
  • Înțelegeți datele relevante și utilizați-le pentru prezicerea informațiilor utile.
  • Procesul de predicție a deciziilor informate este accelerat .

Exploatarea datelor poate fi denumită și procesul de identificare a tiparelor ascunse de informații care necesită clasificare. Numai atunci datele pot fi convertite în date utile. Datele utile pot fi introduse într-un depozit de date, algoritmi de extragere a datelor, analiza datelor pentru luarea deciziilor.

Arborele de decizie în data mining

Un tip de tehnică de data mining, Arborele de decizie în data mining construiește un model pentru clasificarea datelor. Modelele sunt construite sub forma structurii arborescente și, prin urmare, aparțin formei de învățare supravegheată. În afară de modelele de clasificare, arborii de decizie sunt utilizați pentru a construi modele de regresie pentru prezicerea etichetelor de clasă sau a valorilor care ajută procesul de luare a deciziilor. Atât datele numerice, cât și cele categoriale, cum ar fi sexul, vârsta etc., pot fi utilizate de un arbore de decizie.

Structura unui arbore de decizie

Structura unui arbore de decizie constă dintr-un nod rădăcină, ramuri și noduri frunză. Nodurile ramificate sunt rezultatele unui arbore, iar nodurile interne reprezintă testul asupra unui atribut. Nodurile frunză reprezintă o etichetă de clasă.

Funcționarea unui arbore de decizie

1. Un arbore de decizie funcționează sub abordarea învățării supravegheate atât pentru variabile discrete, cât și pentru variabile continue. Setul de date este împărțit în subseturi pe baza celui mai semnificativ atribut al setului de date. Identificarea atributului și împărțirea se face prin algoritmi.

2. Structura arborelui de decizie constă din nodul rădăcină, care este nodul predictor semnificativ. Procesul de divizare are loc din nodurile de decizie care sunt sub-nodurile arborelui. Nodurile care nu se împart în continuare sunt denumite noduri de frunză sau terminale.

3. Setul de date este împărțit în regiuni omogene și care nu se suprapun în urma unei abordări de sus în jos. Stratul superior oferă observațiile într-un singur loc care apoi se împarte în ramuri. Procesul este denumit „Abordare lacomă” datorită concentrării sale doar asupra nodului actual, mai degrabă decât asupra nodurilor viitoare.

4. Până când și dacă nu se atinge un criteriu de oprire, arborele de decizie va continua să ruleze.

5. Odată cu construirea unui arbore de decizie, se generează mult zgomot și valori aberante. Pentru a elimina aceste valori aberante și date zgomotoase, se aplică o metodă de „Tăiere a copacilor”. Prin urmare, acuratețea modelului crește.

6. Acuratețea unui model este verificată pe un set de testare format din tupluri de testare și etichete de clasă. Un model precis este definit pe baza procentelor de tuplu și clase ale setului de test de clasificare de către model.

Figura 1 : Un exemplu de copac netuns și tăiat

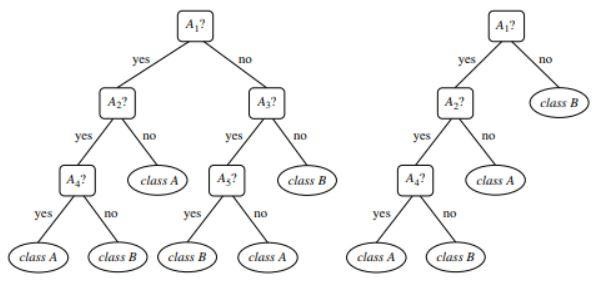
Sursă

Tipuri de arbore decizional

Arborele de decizie duc la dezvoltarea modelelor de clasificare și regresie bazate pe o structură asemănătoare arborelui. Datele sunt împărțite în subseturi mai mici. Rezultatul unui arbore de decizie este un arbore cu noduri de decizie și noduri de frunze. Două tipuri de arbori de decizie sunt explicate mai jos:

1. Clasificare

Clasificarea include construirea de modele care descriu etichete importante de clasă. Ele sunt aplicate în domeniile învățării automate și recunoașterii modelelor. Arborele de decizie în învățarea automată prin modele de clasificare duc la detectarea fraudei, diagnosticarea medicală etc. Procesul în două etape a unui model de clasificare include:

• Învățare: se construiește un model de clasificare bazat pe datele de antrenament.
• Clasificare: acuratețea modelului este verificată și apoi utilizată pentru clasificarea noilor date. Etichetele de clasă sunt sub formă de valori discrete precum „da” sau „nu”, etc.

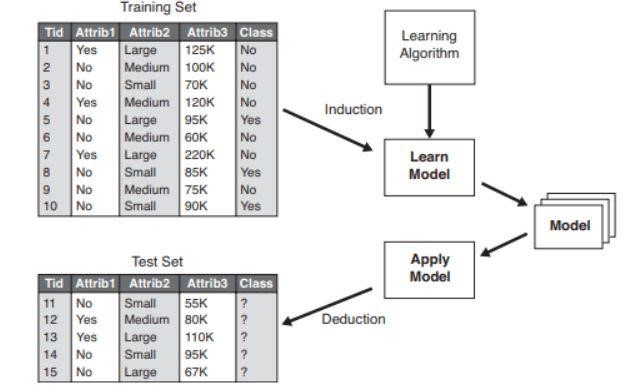
Figura 2 : Exemplu de model de clasificare .

Sursă

2. Regresia

Modelele de regresie sunt folosite pentru analiza de regresie a datelor, adică predicția atributelor numerice. Acestea se mai numesc și valori continue. Prin urmare, în loc să prezică etichetele clasei, modelul de regresie prezice valorile continue.

Lista algoritmilor utilizați

Un algoritm de arbore de decizie cunoscut sub numele de „ID3” a fost dezvoltat în 1980 de un cercetător de mașini pe nume, J. Ross Quinlan. Acest algoritm a fost succedat de alți algoritmi precum C4.5 dezvoltat de el. Ambii algoritmi au aplicat abordarea greedy. Algoritmul C4.5 nu folosește backtracking și copacii sunt construiți într-o manieră recursivă de sus în jos împărți și cuceri. Algoritmul a folosit un set de date de antrenament cu etichete de clasă care sunt împărțite în subseturi mai mici pe măsură ce arborele este construit.

• Sunt selectați inițial trei parametri: lista de atribute, metoda de selecție a atributelor și partiția de date. Atributele setului de antrenament sunt descrise în lista de atribute.
• Metoda de selecție a atribuirii include metoda de selecție a celui mai bun atribut pentru discriminarea între tupluri.
• O structură arborescentă depinde de metoda de selecție a atributelor.
• Construcția unui arbore începe cu un singur nod.
• Divizarea tuplurilor are loc atunci când într-un tuplu sunt reprezentate diferite etichete de clasă. Acest lucru va duce la formarea ramurilor copacului.
• Metoda de împărțire determină ce atribut trebuie selectat pentru partiția de date. Pe baza acestei metode, ramurile sunt crescute dintr-un nod pe baza rezultatului testului.
• Metoda de împărțire și partiționare este efectuată recursiv, rezultând în cele din urmă un arbore de decizie pentru tuplurile setului de date de antrenament.
• Procesul de formare a copacilor continuă până când și cu excepția cazului în care tuplurile rămase nu pot fi împărțite în continuare.
• Complexitatea algoritmului se notează prin

n * |D| * jurnal |D|

Unde, n este numărul de atribute din setul de date de antrenament D și |D| este numărul de tupluri.

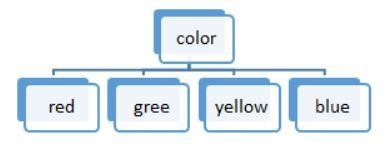
Sursă

Figura 3: O împărțire a valorii discrete

Listele de algoritmi utilizați într-un arbore de decizie sunt:

ID3

Întregul set de date S este considerat nodul rădăcină în timp ce formează arborele de decizie. Iterația este apoi efectuată pentru fiecare atribut și împărțirea datelor în fragmente. Algoritmul verifică și preia acele atribute care nu au fost preluate înainte de cele repetate. Împărțirea datelor în algoritmul ID3 necesită mult timp și nu este un algoritm ideal, deoarece depășește datele.

C4.5

Este o formă avansată de algoritm, deoarece datele sunt clasificate ca eșantioane. Atât valorile continue, cât și cele discrete pot fi gestionate eficient, spre deosebire de ID3. Există o metodă de tăiere care îndepărtează ramurile nedorite.

CART

Atât sarcinile de clasificare, cât și cele de regresie pot fi efectuate de algoritm. Spre deosebire de ID3 și C4.5, punctele de decizie sunt create luând în considerare indicele Gini. Se aplică un algoritm greedy pentru metoda de împărțire care urmărește reducerea funcției de cost. În sarcinile de clasificare, indicele Gini este utilizat ca funcție de cost pentru a indica puritatea nodurilor frunzelor. În sarcinile de regresie, eroarea sumă pătrată este utilizată ca funcție de cost pentru a găsi cea mai bună predicție.

CHAID

După cum sugerează și numele, reprezintă detectorul automat de interacțiune chi-pătrat, un proces care se ocupă cu orice tip de variabile. Acestea pot fi variabile nominale, ordinale sau continue. Arborii de regresie folosesc testul F, în timp ce testul Chi-pătrat este utilizat în modelul de clasificare.

MARTE

Acesta reprezintă spline de regresie adaptativă multivariată. Algoritmul este implementat special în sarcinile de regresie, unde datele sunt în mare parte neliniare.

Divizarea binară recursive greedy

Are loc o metodă de împărțire binară, rezultând două ramuri. Împărțirea tuplurilor se realizează cu calculul funcției de cost divizat. Este selectată cea mai mică împărțire a costurilor și procesul este efectuat recursiv pentru a calcula funcția de cost a celorlalte tupluri.

Arborele de decizie cu exemplu din lumea reală

Preziceți procesul de eligibilitate pentru împrumut din datele date.

Pasul 1: Încărcarea datelor

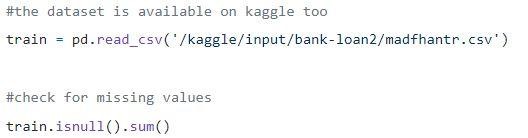
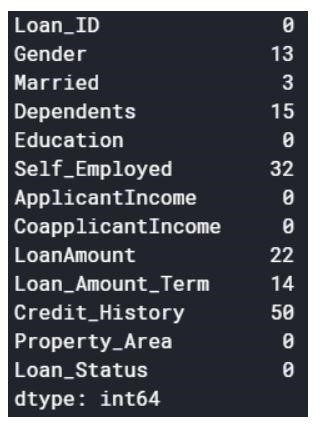
Valorile nule pot fi fie eliminate, fie completate cu unele valori. Forma setului de date original a fost (614,13), iar noul set de date după eliminarea valorilor nule este (480,13).

Pasul 2: o privire asupra setului de date.

Pasul 3: Împărțirea datelor în seturi de antrenament și de testare.

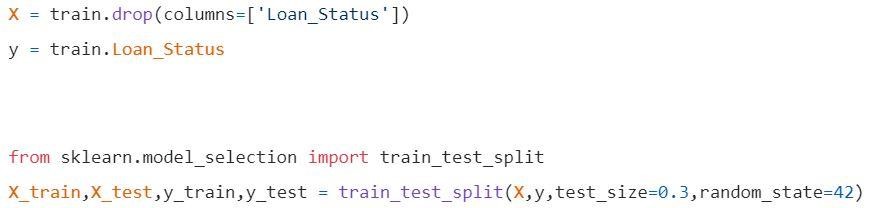
Pasul 4: Construiți modelul și montați setul de tren

Înainte de vizualizare trebuie făcute unele calcule.

Calcul 1: calculați entropia setului de date total.

Calcul 2: Găsiți entropia și câștigul pentru fiecare coloană.

1. Coloana Sex

• Condiția 1: set de date cu toți bărbații în el și apoi,

p = 278, n=116, p+n=489

Entropie (G = Masculin) = 0,87

• Condiția 2: set de date cu toate femeile în el și apoi,

p = 54, n = 32, p+n = 86

Entropie (G=femeie) = 0,95

• Informații medii în coloana de gen

2. Coloana Căsătorit

• Condiția 1: Căsătorit = Da (1)

În această împărțire, întregul set de date cu statutul de Căsătorit, da

p = 227, n = 84, p+n = 311

E(Căsătorit = Da) = 0,84

• Condiția 2: Căsătorit = Nu (0)

În această împărțire, întregul set de date cu statutul de Căsătorit nr

p = 105, n = 64, p+n = 169

E(Căsătorit = Nu) = 0,957

• Informațiile medii din coloana Căsătorit sunt

3. Rubrica educațională

• Condiția 1: Educație = Absolvent(1)

p = 271, n = 112, p+n = 383

E(Educație = Absolvent) = 0,87

• Condiția 2: Educație = Nu absolvent(0)

p = 61, n = 36, p+n = 97

E (Educație = Nu absolvent) = 0,95

• Coloana Informații medii despre educație= 0,886

Câștig = 0,01

4) Coloana Independenți

• Condiția 1: lucrător pe cont propriu = Da (1)

p = 43, n = 23, p+n = 66

E(independenți=Da) = 0,93

• Condiția 2: lucrător pe cont propriu = Nu (0)

p = 289, n = 125, p+n = 414

E(Independenți=Nu) = 0,88

• Informații medii în coloana Independenți în educație = 0,886

Câștig = 0,01

5. Coloana Scor de credit: coloana are valoarea 0 și 1.

• Condiția 1: Scorul de credit = 1

p = 325, n = 85, p+n = 410

E(Scor de credit = 1) = 0,73

• Condiția 2: Scorul de credit = 0

p = 63, n = 7, p+n = 70

E(Scor de credit = 0) = 0,46

• Informații medii în coloana Scor de credit = 0,69

Câștig = 0,2

Comparați toate valorile câștigului

Scorul de credit are cel mai mare câștig. Prin urmare, va fi folosit ca nod rădăcină.

Pasul 5: Vizualizați arborele de decizie

Figura 5: Arborele de decizie cu criteriul Gini

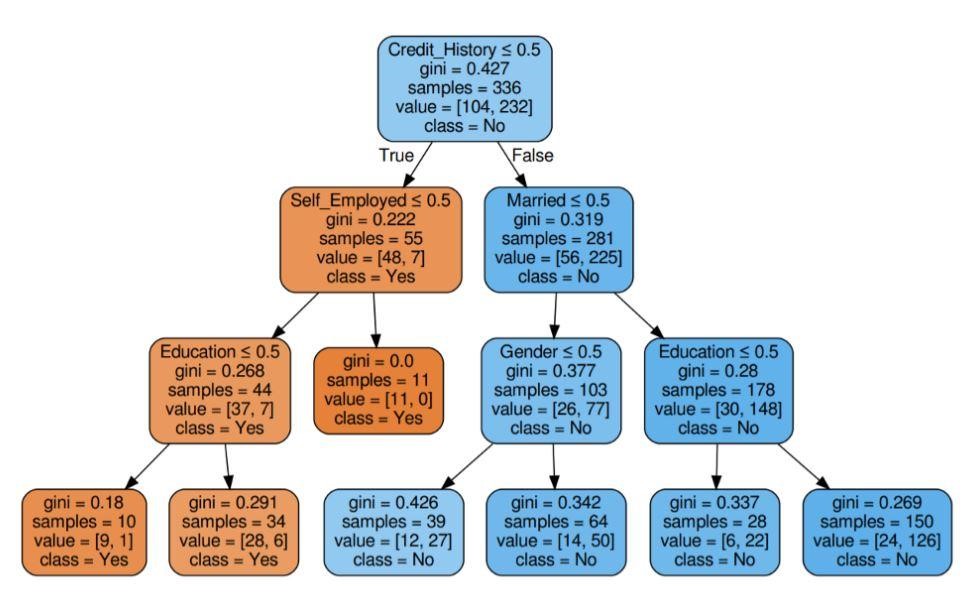Sursă

Figura 6: Arborele de decizie cu criteriul de entropie

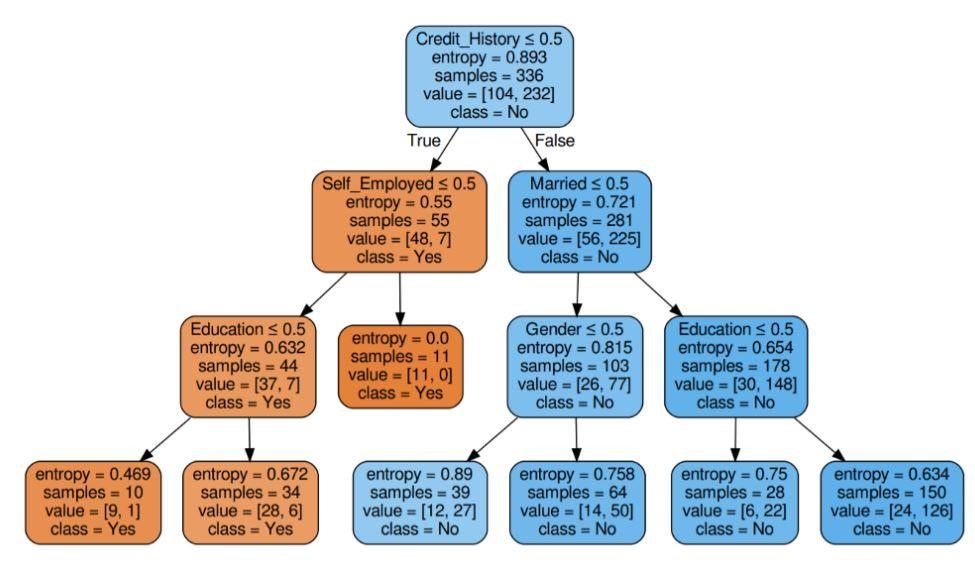
Sursă

Pasul 6: Verificați scorul modelului

Aproape 80% la sută de precizie a marcat.

Lista aplicațiilor

Arborele de decizie sunt utilizați în cea mai mare parte de experții în informații pentru a efectua o investigație analitică. Acestea pot fi utilizate pe scară largă în scopuri de afaceri pentru a analiza sau prezice dificultăți. Flexibilitatea arborelui de decizie le permite să fie utilizate într-o zonă diferită:

1. Asistență medicală

Arborele de decizie permit predicția dacă un pacient suferă de o anumită boală cu condiții de vârstă, greutate, sex etc. Alte predicții includ deciderea efectului medicamentului luând în considerare factori precum compoziția, perioada de fabricație etc.

2. Sectoarele bancare

Arborele de decizie ajută la prezicerea dacă o persoană este eligibilă pentru un împrumut având în vedere starea sa financiară, salariul, membrii familiei etc. Poate identifica, de asemenea, fraudele cu cardul de credit, neplata împrumutului etc.

3. Sectoarele educaționale

Lista scurtă a unui student pe baza punctajului său de merit, prezență etc. poate fi decisă cu ajutorul arborilor de decizie.

Lista de avantaje

• Rezultatele interpretabile ale unui model de decizie pot fi prezentate conducerii superioare și părților interesate.
• În timpul construirii unui model de arbore de decizie, preprocesarea datelor, adică normalizarea, scalarea etc. nu este necesară.
• Ambele tipuri de date - numerice și categorice pot fi gestionate de un arbore de decizie care afișează eficiența sa mai mare de utilizare față de alți algoritmi.
• Valoarea lipsă în date nu afectează procesul unui arbore de decizie, făcându-l astfel un algoritm flexibil.

Ce urmează?

Dacă sunteți interesat să obțineți experiență practică în mineritul de date și să vă instruiți de către experți în domeniul științei datelor, puteți consulta Programul Executive PG în știința datelor de la upGrad. Cursul este destinat oricărei grupe de vârstă cu vârsta cuprinsă între 21-45 de ani, cu criterii minime de eligibilitate de 50% sau note de trecere echivalente la absolvire. Orice profesionist care lucrează se poate alătura acestui program executiv PG certificat de IIIT Bangalore.