Ce este gândirea bayesiană? Introducere și Teoremă

O teoremă statistică dată de statisticianul și filozoful englez Thomas Bayes în anii 1700 continuă să fie o lumină călăuzitoare pentru oamenii de știință și analiștii din întreaga lume. Astăzi, gândirea bayesiană își găsește aplicare în medicină, știință, tehnologie și alte câteva discipline și continuă să ne influențeze puternic viziunea asupra lumii și acțiunile rezultate.

Ideea lui Thomas Bayes a fost izbitor de simplă. Potrivit lui Bayes, probabilitatea ca o ipoteză să fie adevărată depinde de două condiții: cât de rezonabilă este bazată pe ceea ce știm deja (cunoștințele anterioare) și cât de bine se potrivește cu noi dovezi. Astfel, gândirea bayesiană diferă de testarea tradițională a ipotezelor prin aceea că prima include cunoștințele anterioare înainte de a sari la concluzii.

Având în vedere introducerea preliminară, haideți să ne aprofundăm puțin mai multe despre statisticile bayesiene.

Statistica Bayesiană

În termeni simpli, statistica bayesiană aplică probabilități problemelor statistice pentru a actualiza convingerile anterioare în lumina dovezilor de date noi. Probabilitatea exprimă un grad de credință într-un anumit eveniment.

Gradul de credință se poate baza pe cunoștințele anterioare despre eveniment, bazate pe presupuneri personale sau pe rezultatele experimentelor anterioare. Statistica bayesiană utilizează teorema lui Bayes pentru a calcula probabilitățile. Teorema lui Bayes, la rândul său, descrie probabilitatea condiționată a unui eveniment pe baza unor noi dovezi și informații anterioare legate de eveniment.

Având acest lucru în minte, haideți să reluăm conceptul fundamental de probabilitate condiționată înainte de a înțelege în profunzime teorema lui Bayes.

Probabilitate condițională

Probabilitatea condiționată poate fi definită ca probabilitatea unui eveniment sau a unui rezultat bazat pe apariția unui eveniment sau a unui rezultat anterior. Se calculează înmulțind probabilitatea evenimentului anterior cu probabilitatea evenimentului ulterior sau condiționat.

Să aruncăm o privire la un exemplu pentru a înțelege mai bine conceptul .

• Evenimentul A este că o familie care planifica o ieșire va merge la un picnic. Există o șansă de 80% ca familia să meargă la picnic.
• Evenimentul B este că va ploua în ziua în care familia iese la picnic. Prognoza meteo spune că există 60% șanse de precipitații în ziua de picnic.
• Prin urmare, probabilitatea (P) ca familia să meargă la picnic și să plouă se calculează după cum urmează:

P (Picnic și ploaie) = P (Ploaie | Picnic) P (Picnic) = (0,60) * (0,80) = 0,48

În exemplul de mai sus, probabilitatea condiționată privește cele două evenimente A și B în relație unul cu celălalt, adică probabilitatea ca familia să meargă la picnic și, de asemenea, să plouă în aceeași zi.

Prin urmare, probabilitatea condiționată diferă de probabilitatea necondiționată deoarece aceasta din urmă se referă la probabilitatea de apariție a unui eveniment, indiferent dacă orice alt eveniment sau evenimente au avut loc sau sunt prezente orice alte condiții.

Formula probabilității condiționate

Formula pentru probabilitatea condiționată provine din regula înmulțirii probabilității:

P (A și B) sau P (AUB) = P ( B dat A) sau P (B | A) * P (A)

În ecuația de mai sus, P (A și B) este probabilitatea comună, referindu-se la probabilitatea ca două sau mai multe evenimente să se producă simultan. Se mai scrie ca P (A,B).

Iată cum se deduce ecuația probabilității condiționate din regula înmulțirii:

Pasul 1: Notați regula înmulțirii.

P (A și B) = P (B | A) * P (A)

Pasul 2: Împărțiți ambele părți ale ecuației la P (A).

P (A și B) / P (A) = P (B | A) * P (A) / P (A)

Pasul 3: Anulați P (A) din partea dreaptă a ecuației.

P (A și B) / P (A) = P (B | A)

Pasul 4: Rescrie ecuația.

P (A și B) = P (B | A) / P (A)

Astfel, formula probabilității condiționate este dată astfel:

P (A și B) = P (B | A) / P (A)

Teorema lui Bayes

Folosind teorema lui Bayes, ne putem actualiza convingerile și convingerile pe baza unor dovezi noi și relevante. De exemplu, dacă încercăm să ne dăm seama care este probabilitatea ca o anumită persoană să aibă cancer, în general am presupune că acesta este procentul din populație care are cancer. Cu toate acestea, dacă introducem dovezi suplimentare, cum ar fi persoana în cauză este un fumător obișnuit, ne putem actualiza percepția (și, prin urmare, probabilitatea), deoarece probabilitatea de a avea cancer este mai mare dacă un individ este fumător. Prin urmare, folosim atât cunoștințele noastre anterioare, cât și dovezile suplimentare pentru a ne îmbunătăți estimările.

Formula pentru teorema lui Bayes

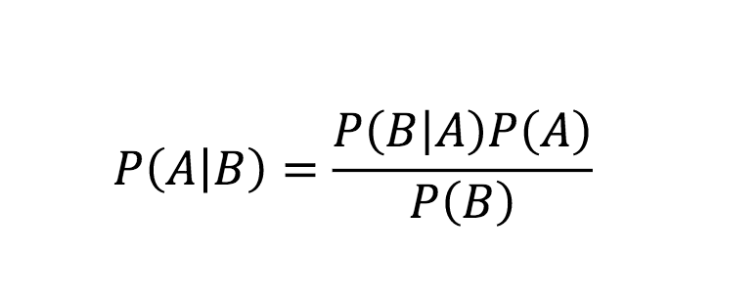
Sursă

Ecuația de mai sus este regula lui Bayes. Acum, să ne uităm la derivarea treptată a ecuației teoremei lui Bayes.

Pasul 1: Luați în considerare două evenimente, A și B. A este evenimentul a cărui probabilitate dorim să o calculăm și B este dovada suplimentară care este legată de A.

Pasul 2: Notați relația dintre probabilitatea comună și probabilitatea condiționată a evenimentelor A și B.

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

Pasul 3: Setați cei doi termeni de probabilitate condiționali egali unul cu celălalt.

P (A | B) * P(B) = P (B | A) * P(A)

Pasul 4: Împărțiți ambele părți ale ecuației la P (B).

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

Pasul 5: Anulați P (B) din partea stângă a ecuației.

P (A | B) = P (B | A) * P(A) / P (B)

Astfel, obținem formula teoremei lui Bayes după cum urmează:

P (A | B) = P (B | A) * P(A) / P (B)

Înțelegerea termenilor din ecuația teoremei lui Bayes

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B) se numește probabilitatea posterioară sau probabilitatea pe care încercăm să o estimăm. Pe baza exemplului anterior, probabilitatea posterioara ar fi probabilitatea ca persoana sa aiba cancer, in conditiile in care persoana respectiva este un fumator obisnuit.
• P (B | A) se numește probabilitate , referindu-se la probabilitatea de a detecta dovezi suplimentare, având în vedere ipoteza noastră inițială. În exemplul de mai sus, probabilitatea este probabilitatea ca persoana să fie fumătoare, având în vedere că persoana are cancer.
• P (A) este probabilitatea anterioară sau probabilitatea ipotezei noastre fără nicio dovadă sau informații suplimentare. În exemplul de mai sus, probabilitatea anterioară este probabilitatea de a avea cancer.
• P (B) este probabilitatea marginală sau probabilitatea totală de a observa dovezile. În contextul exemplului de mai sus, probabilitatea marginală este probabilitatea de a fi fumător.

Un exemplu simplu pentru a înțelege teorema lui Bayes

Folosind câteva numere ipotetice din exemplul anterior, vom vedea efectul aplicării teoremei lui Bayes.

Să presupunem că probabilitatea de a avea cancer este de 0,06, adică 6% dintre oameni au cancer. Acum, să spunem că probabilitatea de a fi fumător este de 0,20 sau 20% dintre oameni sunt fumători, iar 30% dintre persoanele cu cancer sunt fumători. Deci, P (Fumător | Cancer) = 0,30.

Inițial, probabilitatea de a avea cancer este pur și simplu de 0,06 (anterior). Dar folosind noile dovezi, putem calcula P (Rac | Fumător) = P ((Fumător | Rac) * P (Rac)) / P (Fumător) = (0,30*0,06) / (0,20) = 0,09.

Învață cursuri de știință a datelor online de la cele mai bune universități din lume. Câștigă programe Executive PG, programe avansate de certificat sau programe de master pentru a-ți accelera cariera.

Calea de urmat: Stăpânește conceptele de statistică pentru o carieră în știința datelor sau în învățarea automată

Platforma de învățare EdTech superior a upGrad a afectat peste 500.000 de profesioniști din întreaga lume cu multitudinea de cursuri și experiențe de învățare captivante. Cu o bază de peste 40.000 de cursanți răspândiți în peste 85 de țări, cursurile upGrad relevante pentru industrie sunt garantate pentru a vă avansa cariera în domeniul pe care îl alegeți.

Master of Science in Data Science este un curs de 18 luni care oferă abilități cheie în statistică, analiză predictivă, învățare automată, analiză a datelor mari, vizualizare a datelor etc.

Repere ale programului:

• Master de la Liverpool John Moores University și Executive PGP de la IIIT Bangalore
• Peste 500 de ore de conținut, peste 60 de studii de caz și proiecte, peste 20 de sesiuni live, peste 14 limbaje și instrumente de programare
• Rețele din industrie, sesiuni de rezolvare a îndoielilor și sprijin pentru învățare

Programul de certificat avansat în Învățare automată și Învățare profundă este un curs riguros de 6 luni, cu oportunități de relații între colegi, proiecte practice, mentorat în industrie și asistență în carieră la 360 de grade.

Repere ale programului:

• Recunoaștere de prestigiu de la IIIT Bangalore
• Peste 240 de ore de conținut, peste 5 studii de caz și proiecte, peste 24 de sesiuni live, acoperire a 12 limbaje de programare, instrumente și biblioteci
• Sesiuni de coaching de grup 1:8 și sesiuni de mentorat 1:1 cu experți din industrie

Concluzie

Gândirea bayesiană stă la baza mai multor domenii ale gândirii umane, anchetei și credinței, chiar dacă cei mai mulți dintre noi nu suntem conștienți de aceasta. De la screening-ul cancerului și încălzirea globală până la politica monetară și evaluarea riscurilor și asigurări , gândirea bayesiană este fundamentală. Chiar și faimosul matematician britanic Alan Turing se crede că a folosit abordarea bayesiană pentru a sparge Codul Enigma German în timpul celui de-al Doilea Război Mondial.

Înscrieți-vă la upGrad și îmbunătățiți-vă cunoștințele despre conceptele statistice cheie și multe altele!