Învață algoritmul naiv Bayes pentru învățarea automată [cu exemple]
Publicat: 2021-02-25Cuprins
Introducere
În matematică și programare, unele dintre cele mai simple soluții sunt de obicei cele mai puternice. Algoritmul naiv Bayes vine ca un exemplu clasic al acestei afirmații. Chiar și cu progresul și dezvoltarea puternică și rapidă în domeniul învățării automate, acest algoritm naiv Bayes rămâne puternic ca unul dintre cei mai folosiți și eficienți algoritmi. Algoritmul Bayes naiv își găsește aplicațiile într-o varietate de probleme, inclusiv sarcini de clasificare și probleme de procesare a limbajului natural (NLP).
Ipoteza matematică a teoremei Bayes servește drept concept fundamental din spatele acestui algoritm naiv Bayes. În acest articol, vom trece prin elementele de bază ale teoremei Bayes, algoritmul naiv Bayes, împreună cu implementarea sa în Python, cu un exemplu de problemă în timp real. Alături de acestea, vom analiza și câteva avantaje și dezavantaje ale algoritmului Naive Bayes în comparație cu concurenții săi.
Bazele probabilității
Înainte să ne aventurăm să înțelegem teorema Bayes și algoritmul naiv Bayes, să ne perfecționăm cunoștințele existente cu privire la fundamentele probabilității.
După cum știm cu toții prin definiție, dat fiind un eveniment A, probabilitatea ca acel eveniment să se producă este dată de P(A). În probabilitate, două evenimente A și B sunt denumite evenimente independente dacă apariția evenimentului A nu modifică probabilitatea de apariție a evenimentului B și invers. Pe de altă parte, dacă apariția unuia schimbă probabilitatea celuilalt, atunci acestea sunt denumite evenimente dependente.
Să fim introduși într-un nou termen numit Probabilitate condiționată . În matematică, Probabilitatea condiționată pentru două evenimente A și B date de P (A| B) este definită ca probabilitatea de apariție a evenimentului A dat fiind că evenimentul B a avut deja loc. În funcție de relația dintre cele două evenimente A și B, dacă sunt dependente sau independente, probabilitatea condiționată este calculată în două moduri.
- Probabilitatea condiționată a două evenimente dependente A și B este dată de P (A| B) = P (A și B) / P (B)
- Expresia pentru probabilitatea condiționată a două evenimente independente A și B este dată de, P (A| B) = P (A)
Cunoscând matematica din spatele Probabilității și Probabilităților Condiționale, să trecem acum la Teorema Bayes.

Teorema Bayes
În statistică și teoria probabilității, teorema lui Bayes, cunoscută și sub numele de regula lui Bayes, este folosită pentru a determina probabilitatea condiționată a evenimentelor. Cu alte cuvinte, teorema lui Bayes descrie probabilitatea unui eveniment pe baza cunoașterii anterioare a condițiilor care ar putea fi relevante pentru eveniment.
Pentru a o înțelege într-un mod mai simplu, luați în considerare că trebuie să știm că probabilitatea ca prețul unei case să fie foarte mare. Dacă știm despre ceilalți parametri, cum ar fi prezența școlilor, magazinelor medicale și spitalelor din apropiere, atunci putem face o evaluare mai precisă a acestora. Aceasta este exact ceea ce efectuează teorema Bayes.
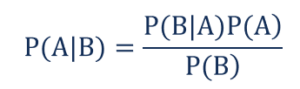
Astfel încât,
- P(A|B) – probabilitatea condiționată de apariție a evenimentului A, dat fiind că evenimentul B a avut loc, cunoscut și sub numele de Probabilitate Posterior .
- P(B|A) – probabilitatea condiționată de apariție a evenimentului B, dat fiind că a avut loc evenimentul A, cunoscut și sub denumirea de probabilitate de probabilitate .
- P(A) – probabilitatea ca evenimentul A să se producă, cunoscută și sub denumirea de probabilitate anterioară.
- P(B) – probabilitatea ca evenimentul B să se producă, cunoscută și sub numele de Probabilitate marginală.
Să presupunem că avem o problemă simplă de învățare automată cu „n” variabile independente și variabila dependentă care este rezultatul este o valoare booleană (adevărat sau fals). Să presupunem că atributele independente sunt de natură categorială, să luăm în considerare 2 categorii pentru acest exemplu. Prin urmare, cu aceste date, trebuie să calculăm valoarea probabilității probabilității, P(B|A).
Prin urmare, observând cele de mai sus, constatăm că trebuie să calculăm 2*(2^ n -1 ) parametri pentru a învăța acest model de învățare automată. În mod similar, dacă avem 30 de atribute booleene independente, atunci numărul total de parametri de calculat va fi aproape de 3 miliarde, ceea ce este extrem de mare în ceea ce privește costul de calcul.
Această dificultate în construirea unui model de învățare automată cu teorema Bayes a condus la nașterea și dezvoltarea algoritmului naiv Bayes.
Algoritmul naiv Bayes
Pentru a fi practic, complexitatea menționată mai sus a teoremei Bayes trebuie redusă. Acest lucru se realizează exact în algoritmul naiv Bayes făcând câteva presupuneri. Ipotezele făcute sunt că fiecare caracteristică aduce o contribuție independentă și egală la rezultat.
Algoritmul Bayes naiv este un algoritm de învățare supravegheată și se bazează pe teorema Bayes, care este folosită în principal în rezolvarea problemelor de clasificare. Este unul dintre cei mai simpli și mai precisi clasificatori care construiesc modele de învățare automată pentru a face predicții rapide. Din punct de vedere matematic, este un clasificator probabilist, deoarece face predicții folosind funcția de probabilitate a evenimentelor.
Exemplu de problemă
Pentru a înțelege logica din spatele ipotezelor, să trecem printr-un set de date simplu pentru a obține o intuiție mai bună.
| Culoare | Tip | Origine | Furt? |
| Negru | Sedan | Importat | da |
| Negru | SUV | Importat | Nu |
| Negru | Sedan | Intern | da |
| Negru | Sedan | Importat | Nu |
| Maro | SUV | Intern | da |
| Maro | SUV | Intern | Nu |
| Maro | Sedan | Importat | Nu |
| Maro | SUV | Importat | da |
| Maro | Sedan | Intern | Nu |
Din setul de date prezentat mai sus, putem deriva conceptele celor două ipoteze pe care le-am definit mai sus pentru algoritmul Naive Bayes.
- Prima presupunere este că toate caracteristicile sunt independente unele de altele. Aici, vedem că fiecare atribut este independent, cum ar fi culoarea „Roșu” este independentă de Tipul și Originea mașinii.
- În continuare, fiecărei caracteristici trebuie să i se acorde o importanță egală. În mod similar, doar cunoștințele despre tipul și originea mașinii nu sunt suficiente pentru a prezice rezultatul problemei. Prin urmare, niciuna dintre variabile nu este irelevantă și, prin urmare, toate au o contribuție egală la rezultat.
Pentru a rezuma, A și B sunt independenți condiționat, dat fiind C, dacă și numai dacă, având în vedere că are loc C, cunoașterea dacă apare A nu oferă informații despre probabilitatea ca B să apară, iar cunoașterea dacă apare B nu oferă informații despre probabilitatea ca A să apară. Aceste ipoteze fac ca algoritmul Bayes să fie naiv . De aici și numele, Naive Bayes Algorithm.
Prin urmare, pentru problema de mai sus, teorema Bayes poate fi rescrisă ca -
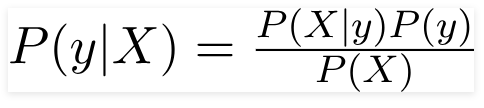
Astfel încât,
- Vectorul de caracteristică independent, X = (x 1 , x 2 , x 3 ……x n ) reprezentând caracteristici precum culoarea, tipul și originea mașinii.
- Variabila de ieșire, y are doar două rezultate Da sau Nu.
Prin urmare, prin înlocuirea valorilor de mai sus, obținem formula Naive Bayes ca:
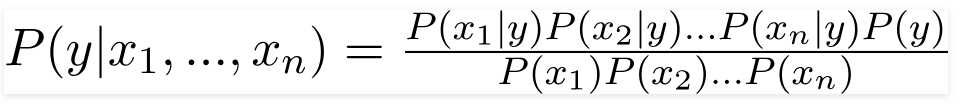
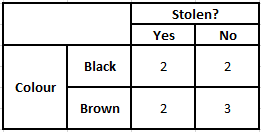
Pentru a calcula probabilitatea posterioară P(y|X), trebuie să creăm un tabel de frecvență pentru fiecare atribut față de rezultat. Apoi convertim tabelele de frecvență în tabele de probabilitate, după care folosim în cele din urmă ecuația Bayesiană Naive pentru a calcula probabilitatea posterioară pentru fiecare clasă. Clasa cu cea mai mare probabilitate posterioară este aleasă ca rezultat al predicției. Mai jos sunt tabelele de frecvență și probabilitate pentru toți cei trei predictori.
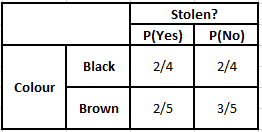
Tabelul de frecvență al culorilor Tabelul probabilității culorilor
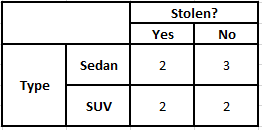
Tabelul de frecvență al tipului Tabelul probabilității tipului

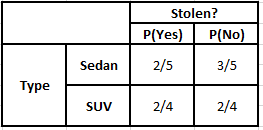
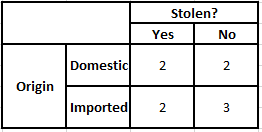
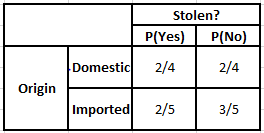
Tabelul de frecvență a originii Tabelul de probabilitate a originii
Luați în considerare cazul în care trebuie să calculăm probabilitățile posterioare pentru condițiile de mai jos -
| Culoare | Tip | Origine |
| Maro | SUV | Importat |
Astfel, din formula dată mai sus, putem calcula probabilitățile posterioare așa cum se arată mai jos -
P(Da | X) = P(Maro | Da) * P(SUV | Da) * P(Importat | Da) * P(Da)
= 2/5 * 2/4 * 2/5 * 1
= 0,08
P(Nu | X) = P(Maro | Nu) * P(SUV | Nu) * P(Importat | Nu) * P(Nu)
= 3/5 * 2/4 * 3/5 * 1
= 0,18
Din valorile calculate mai sus, deoarece probabilitățile posterioare pentru Nu sunt mai mari decât Da (0,18>0,08), atunci se poate deduce că o mașină cu culoare maro, tip SUV de origine importată este clasificată ca „Nu”. Prin urmare, mașina nu este furată.
Implementare în Python
Acum că am înțeles matematica din spatele algoritmului Naive Bayes și am vizualizat-o, de asemenea, cu un exemplu, să trecem prin codul său de Machine Learning în limbajul Python.
Înrudit : Naive Bayes Clasifier
Analiza problemei
Pentru a implementa programul Naive Bayes Classification în Machine Learning folosind Python, vom folosi foarte faimosul „Iris Flower Dataset”. Setul de date pentru flori de iris sau setul de date Iris lui Fisher este un set de date multivariate introdus de statisticianul, eugenicianul și biologul britanic Ronald Fisher în 1998. Acesta este un set de date foarte mic și de bază, care constă din date foarte puțin numerice care conțin informații despre 3 clase. de flori aparținând speciei Iris care sunt:
- Iris Setosa
- Iris Versicolour
- Iris Virginica
Există 50 de mostre din fiecare dintre cele trei specii, ceea ce reprezintă un set de date total de 150 de rânduri. Cele 4 atribute (sau) variabile independente care sunt utilizate în acest set de date sunt:
- lungimea sepalului în cm
- latimea sepalului in cm
- lungimea petelor în cm
- latimea petelor in cm
Variabila dependentă este „ specia ” florii care este identificată prin cele patru atribute date de mai sus.
Pasul 1 – Importarea bibliotecilor
Ca întotdeauna, pasul principal în construirea oricărui model de învățare automată va fi importarea bibliotecilor relevante. Pentru aceasta, vom încărca bibliotecile NumPy, Mathplotlib și Pandas pentru preprocesarea datelor.
import numpy ca np
import matplotlib.pyplot ca plt
importa panda ca pd
Pasul 2 - Încărcarea setului de date
Setul de date pentru flori de iris care va fi folosit pentru antrenamentul Naive Bayes Clasifier va fi încărcat într-un Pandas DataFrame. Cele 4 variabile independente vor fi atribuite variabilei X, iar variabila finală specie de ieșire este atribuită lui y.
set de date = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = dataset.iloc[:,:4].values
y = set de date['specie'].valuesdataset.head(5)>>
sepal_length sepal_width petal_length petal_width specie
5,1 3,5 1,4 0,2 setosa
4,9 3,0 1,4 0,2 setosa
4,7 3,2 1,3 0,2 setosa
4,6 3,1 1,5 0,2 setosa
5,0 3,6 1,4 0,2 setosa
Pasul 3 – Împărțirea setului de date în setul de antrenament și setul de testare
După încărcarea setului de date și a variabilelor, următorul pas este pregătirea variabilelor care vor fi supuse procesului de antrenament. În acest pas, trebuie să împărțim variabilele X și y la antrenament și la seturile de date de testare. Pentru aceasta, vom atribui aleatoriu 80% din date setului de antrenament care va fi folosit în scopuri de antrenament și restul de 20% din date ca set de testare pe care va fi testat pentru precizie Clasificatorul Naive Bayes antrenat.
din sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0,2)
Pasul 4 – Scalarea caracteristicilor
Deși acesta este un proces suplimentar pentru acest set de date mic, adaug acest lucru pentru a-l folosi într-un set de date mai mare. În aceasta, datele din seturile de antrenament și de testare sunt reduse la un interval de valori între 0 și 1. Acest lucru reduce costul de calcul.
din sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
Pasul 5 – Antrenarea modelului Naive Bayes Clasificare pe setul de antrenament
În acest pas importăm clasa Naive Bayes din biblioteca sklearn. Pentru acest model, folosim modelul Gaussian, există câteva alte modele precum Bernoulli, Categoric și Multinomial. Astfel, X_train și y_train sunt adaptate la variabila clasificatoare în scopul antrenamentului.
din sklearn.naive_bayes import GaussianNB
clasificator = GaussianNB()
classifier.fit(X_train, y_train)
Pasul 6 – Prezicerea rezultatelor setului de testare –
Previzăm clasa speciei pentru setul de testare folosind modelul antrenat și îl comparăm cu valorile reale ale clasei de specii.
y_pred = clasificator.predict(X_test)
df = pd.DataFrame({'Valori reale':y_test, 'Valori estimate':y_pred})
df>>
Valori reale Valori prezise
setosa setosa
setosa setosa
virginica virginica
versicolor versicolor
setosa setosa
setosa setosa
… … … … …
virginica versicolor
virginica virginica
setosa setosa
setosa setosa
versicolor versicolor
versicolor versicolor
În comparația de mai sus, vedem că există o predicție incorectă care a prezis Versicolor în loc de virginica.
Pasul 7 – Matricea confuziei și acuratețea
Deoarece avem de-a face cu Clasificare, cea mai bună modalitate de a evalua modelul nostru de clasificator este să tipărim Matricea de confuzie împreună cu acuratețea acesteia pe setul de testare.
din sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)din sklearn.metrics import accuracy_score

tipăriți („Precizie: „, scorul_preciziei(y_test, y_pred))
cm>>Precizie : 0,9666666666666667
>>matrice([[14, 0, 0],
[ 0, 7, 0],
[ 0, 1, 8]])
Concluzie
Astfel, în acest articol, am trecut prin elementele de bază ale algoritmului naiv Bayes, am înțeles matematica din spatele clasificării împreună cu un exemplu rezolvat manual. În cele din urmă, am implementat un cod de învățare automată pentru a rezolva un set de date popular folosind algoritmul Naive Bayes Classification.
Dacă sunteți interesat să aflați mai multe despre AI, învățarea automată, consultați Diploma PG de la IIIT-B și upGrad în Învățare automată și AI, care este concepută pentru profesioniști care lucrează și oferă peste 450 de ore de formare riguroasă, peste 30 de studii de caz și sarcini, Statut de absolvenți IIIT-B, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.
Cum este utilă probabilitatea în Machine Learning?
Este posibil să fim nevoiți să luăm decizii bazate pe informații parțiale sau incomplete în scenarii din lumea reală. Probabilitatea ne ajută să cuantificăm incertitudinile din astfel de sisteme și să gestionăm riscul pentru sarcină. Metoda tradițională funcționează numai pentru rezultatele deterministe pentru acțiuni specifice, dar există întotdeauna un anumit domeniu de incertitudine în orice model de predicție. Această incertitudine poate proveni din mulți parametri din datele de intrare, cum ar fi Zgomotul în date. De asemenea, vederile bayesiene din teoremele de probabilitate pot ajuta la recunoașterea modelelor din datele de intrare. Pentru aceasta, probabilitatea folosește conceptul de estimare a probabilității maxime și, prin urmare, este utilă pentru a produce rezultate relevante.
La ce folosește Matricea de confuzie?
Matricea de confuzie este o matrice 2x2 folosită pentru a interpreta performanța modelului de clasificare. Valorile adevărate pentru datele de intrare trebuie să fie cunoscute pentru ca acest lucru să funcționeze, deci nu poate fi reprezentat pentru datele neetichetate. Se compune din numărul de fals pozitive (FP), adevărate pozitive (TP), fals negative (FN) și adevărate negative (TN). Predicțiile sunt clasificate în aceste clase folosind numărul din setul de antrenament și setul de testare. Ne ajută să vizualizăm parametri utili, cum ar fi acuratețea, precizia, reamintirea și specificitatea. Este relativ ușor de înțeles și vă oferă o idee clară despre algoritm.
Care sunt diferitele tipuri de model Naive Bayes?
Toate tipurile se bazează în principal pe teorema Bayes. Modelul Naive Bayes are în general trei tipuri: Gaussian, Bernoulli și Multinomial. Gaussian Naive Bayes ajută cu valori continue din parametrii de intrare și presupune că toate clasele de date de intrare sunt distribuite uniform. Bayesul naiv al lui Bernoulli este un model bazat pe evenimente în care caracteristicile datelor sunt independente și prezente în valori booleene. Multinomial Naive Bayes se bazează, de asemenea, pe un model bazat pe evenimente. Are caracteristicile de date în formă vectorială, care reprezintă frecvențele relevante bazate pe apariția evenimentelor.
