25 Întrebări și răspunsuri la interviu de învățare automată – Regresie liniară
Publicat: 2022-09-08Este o practică comună testarea aspiranților la știința datelor pe algoritmi de învățare automată utilizați în mod obișnuit în interviuri. Acești algoritmi convenționali sunt regresia liniară, regresia logistică, gruparea, arbori de decizie etc. Se așteaptă ca cercetătorii de date să posede o cunoaștere aprofundată a acestor algoritmi.
Am consultat manageri de angajare și oameni de știință ai datelor din diverse organizații pentru a afla despre întrebările tipice ML pe care le pun într-un interviu. Pe baza feedback-ului lor extins, a fost pregătit un set de întrebări și răspunsuri pentru a ajuta aspiranții cercetători de date în conversațiile lor. Întrebările de interviu de regresie liniară sunt cele mai frecvente în interviurile de învățare automată. Întrebările și răspunsurile despre acești algoritmi vor fi furnizate într-o serie de patru postări pe blog.
Cele mai bune cursuri de învățare automată și cursuri AI online
| Master în învățare automată și IA de la LJMU | Program executiv postuniversitar în Machine Learning și AI de la IIITB | |
| Program de certificat avansat în Machine Learning și NLP de la IIITB | Program de certificat avansat în Machine Learning și Deep Learning de la IIITB | Program executiv postuniversitar în știința datelor și învățarea automată de la Universitatea din Maryland |
| Pentru a explora toate cursurile noastre, vizitați pagina noastră de mai jos. | ||
| Cursuri de învățare automată | ||
Fiecare postare de blog va acoperi următorul subiect: -
- Regresie liniara
- Regresie logistică
- Clustering
- Arbori de decizie și întrebări care se referă la toți algoritmii
Să începem cu regresia liniară!
1. Ce este regresia liniară?
În termeni simpli, regresia liniară este o metodă de a găsi cea mai bună potrivire în linie dreaptă la datele date, adică găsirea celei mai bune relații liniare între variabilele independente și dependente.
În termeni tehnici, regresia liniară este un algoritm de învățare automată care găsește cea mai bună relație de potrivire liniară pe orice date date, între variabile independente și dependente. Se realizează în mare parte prin metoda sumei reziduurilor pătrate.
Abilități de învățare automată la cerere
| Cursuri de inteligență artificială | Cursuri Tableau |
| Cursuri NLP | Cursuri de învățare profundă |

2. Prezentați ipotezele într-un model de regresie liniară.
Există trei ipoteze principale într-un model de regresie liniară:
- Ipoteza despre forma modelului:
Se presupune că există o relație liniară între variabilele dependente și independente. Este cunoscută sub numele de „ipoteza de liniaritate”. - Ipoteze despre reziduuri:
- Ipoteza de normalitate: Se presupune că termenii de eroare, ε (i) , sunt distribuiți în mod normal.
- Ipoteza medie zero: Se presupune că reziduurile au o valoare medie de zero.
- Ipoteza de varianță constantă: Se presupune că termenii reziduali au aceeași varianță (dar necunoscută), σ 2 Această ipoteză este cunoscută și sub denumirea de ipoteza de omogenitate sau homoscedasticitate.
- Ipoteza de eroare independentă: Se presupune că termenii reziduali sunt independenți unul de celălalt, adică covarianța lor pe perechi este zero.
- Ipoteze despre estimatori:
- Variabilele independente sunt măsurate fără eroare.
- Variabilele independente sunt liniar independente unele de altele, adică nu există multicoliniaritate în date.
Explicaţie:
- Acest lucru se explică de la sine.
- Dacă reziduurile nu sunt distribuite în mod normal, aleatoritatea lor se pierde, ceea ce implică faptul că modelul nu este capabil să explice relația în date.
De asemenea, media reziduurilor ar trebui să fie zero.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Acesta este modelul liniar presupus, unde ε este termenul rezidual.
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
Dacă așteptarea (media) a reziduurilor, E(ε (i) ), este zero, așteptările variabilei țintă și ale modelului devin aceleași, care este una dintre țintele modelului.
Reziduurile (cunoscute și ca termeni de eroare) ar trebui să fie independente. Aceasta înseamnă că nu există o corelație între reziduuri și valorile prezise sau între reziduurile în sine. Dacă există o corelație, înseamnă că există o relație pe care modelul de regresie nu este capabil să o identifice. - Dacă variabilele independente nu sunt liniar independente unele de altele, se pierde unicitatea soluției celor mai mici pătrate (sau a soluției ecuației normale).
Alăturați-vă Cursului de inteligență artificială online de la cele mai bune universități din lume - Master, programe executive postuniversitare și program de certificat avansat în ML și AI pentru a vă accelera cariera.
3. Ce este ingineria caracteristicilor? Cum îl aplici în procesul de modelare?
Ingineria caracteristicilor este procesul de transformare a datelor brute în caracteristici care reprezintă mai bine problema de bază pentru modelele predictive.
, rezultând o precizie îmbunătățită a modelului pe date nevăzute.
În termeni simpli, ingineria caracteristicilor înseamnă dezvoltarea de noi caracteristici care vă pot ajuta să înțelegeți și să modelați problema într-un mod mai bun. Ingineria caracteristicilor este de două feluri: bazată pe afaceri și bazată pe date. Ingineria de caracteristici bazată pe afaceri se învârte în jurul includerii de caracteristici din punct de vedere al afacerii. Sarcina aici este de a transforma variabilele de afaceri în caracteristici ale problemei. În cazul ingineriei caracteristicilor bazate pe date, caracteristicile pe care le adăugați nu au nicio interpretare fizică semnificativă, dar ajută modelul în predicția variabilei țintă.
FYI: Curs nlp gratuit!
Pentru a aplica ingineria caracteristicilor, trebuie să fiți pe deplin familiarizați cu setul de date. Aceasta implică cunoașterea care sunt datele date, ce înseamnă acestea, care sunt caracteristicile brute etc. De asemenea, trebuie să aveți o idee clară a problemei, cum ar fi ce factori afectează variabila țintă, care este interpretarea fizică a variabilei. , etc.
4. La ce folosește regularizarea? Explicați regularizările L1 și L2.
Regularizarea este o tehnică care este utilizată pentru a aborda problema supraajustării modelului. Atunci când un model foarte complex este implementat pe datele de antrenament, acesta depășește. Uneori, modelul simplu s-ar putea să nu poată generaliza datele, iar modelul complex se supraajustează. Pentru a rezolva această problemă, se utilizează regularizarea.
Regularizarea nu este altceva decât adăugarea termenilor coeficienți (beta) la funcția de cost, astfel încât termenii să fie penalizați și să aibă o amploare mică. Acest lucru ajută, în esență, la captarea tendințelor în date și, în același timp, previne supraadaptarea, nepermițând modelul să devină prea complex.
- Regularizare L1 sau LASSO: Aici, valorile absolute ale coeficienților sunt adăugate la funcția de cost. Acest lucru poate fi văzut în următoarea ecuație; partea evidențiată corespunde regularizării L1 sau LASSO. Această tehnică de regularizare dă rezultate rare, ceea ce duce și la selecția caracteristicilor.
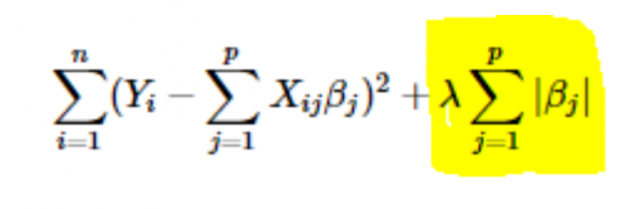
- Regularizare L2 sau Ridge: Aici, pătratele coeficienților sunt adăugate la funcția de cost. Acest lucru poate fi văzut în următoarea ecuație, unde partea evidențiată corespunde regularizării L2 sau Ridge.
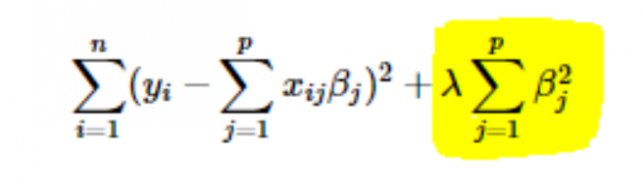
5. Cum să alegeți valoarea ratei de învățare a parametrilor (α)?
Selectarea valorii ratei de învățare este o afacere dificilă. Dacă valoarea este prea mică, algoritmul de coborâre a gradientului durează timp pentru a converge către soluția optimă. Pe de altă parte, dacă valoarea ratei de învățare este mare, coborârea gradientului va depăși soluția optimă și, cel mai probabil, nu va converge niciodată către soluția optimă.
Pentru a depăși această problemă, puteți încerca diferite valori ale alfa într-un interval de valori și puteți reprezenta un grafic costul față de numărul de iterații. Apoi, pe baza graficelor, se poate alege valoarea corespunzătoare graficului care arată scăderea rapidă. 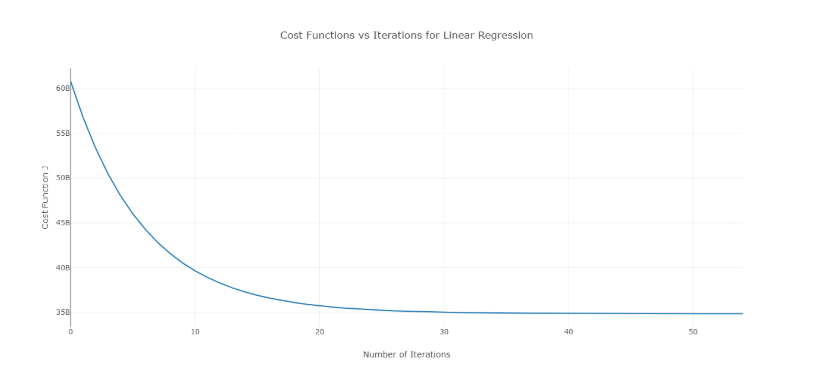
Graficul menționat mai sus este un cost ideal față de curba numărului de iterații. Rețineți că costul scade inițial pe măsură ce numărul de iterații crește, dar după anumite iterații, coborârea gradientului converge și costul nu mai scade.
Dacă observați că costul crește odată cu numărul de iterații, parametrul ratei de învățare este mare și trebuie redus.
6. Cum se alege valoarea parametrului de regularizare (λ)?
Selectarea parametrului de regularizare este o afacere dificilă. Dacă valoarea lui λ este prea mare, se va ajunge la valori extrem de mici ale coeficientului de regresie β , ceea ce va duce la subadaptarea modelului (bias mare – varianță scăzută). Pe de altă parte, dacă valoarea lui λ este 0 (foarte mică), modelul va tinde să depășească datele de antrenament (disturbire scăzută – varianță mare).
Nu există o modalitate corectă de a selecta valoarea lui λ . Ceea ce puteți face este să aveți un sub-eșantion de date și să rulați algoritmul de mai multe ori pe seturi diferite. Aici, persoana trebuie să decidă cât de multă variație poate fi tolerată. Odată ce utilizatorul este mulțumit de varianță, acea valoare a lui λ poate fi aleasă pentru setul de date complet.
Un lucru de remarcat este că valoarea lui λ selectată aici a fost optimă pentru acel subset, nu pentru toate datele de antrenament.
7. Putem folosi regresia liniară pentru analiza seriilor de timp?
Se poate folosi regresia liniară pentru analiza seriilor de timp, dar rezultatele nu sunt promițătoare. Deci, în general, nu este recomandabil să faceți acest lucru. Motivele din spatele acestui lucru sunt:
- Datele din seria temporală sunt utilizate în cea mai mare parte pentru predicția viitorului, dar regresia liniară oferă rareori rezultate bune pentru predicția viitoare, deoarece nu este destinată extrapolării.
- În cea mai mare parte, datele serielor cronologice au un model, cum ar fi în orele de vârf, anotimpurile festive etc., care cel mai probabil ar fi tratate ca valori aberante în analiza regresiei liniare.
8. De ce valoare se apropie suma reziduurilor unei regresii liniare? Justifica.
Răspuns Suma reziduurilor unei regresii liniare este 0. Regresia liniară funcționează din ipoteza că erorile (reziduurile) sunt distribuite în mod normal cu o medie de 0, adică
Y = β T X + ε
Aici, Y este variabila țintă sau dependentă,
β este vectorul coeficientului de regresie,
X este matricea de caracteristici care conține toate caracteristicile sub formă de coloane,
ε este termenul rezidual astfel încât ε ~ N(0,σ 2 ).
Deci, suma tuturor reziduurilor este valoarea așteptată a reziduurilor înmulțită cu numărul total de puncte de date. Deoarece așteptarea reziduurilor este 0, suma tuturor termenilor reziduali este zero.
Notă : N(μ,σ 2 ) este notația standard pentru o distribuție normală având media μ și abaterea standard σ 2 .
9. Cum afectează multicoliniaritatea regresia liniară?
Răspuns Multicoliniaritatea apare atunci când unele dintre variabilele independente sunt foarte corelate (pozitiv sau negativ) între ele. Această multicoliniaritate provoacă o problemă, deoarece este împotriva ipotezei de bază a regresiei liniare. Prezența multicolinearității nu afectează capacitatea de predicție a modelului. Deci, dacă doriți doar predicții, prezența multicolinearității nu vă afectează rezultatul. Cu toate acestea, dacă doriți să extrageți câteva perspective din model și să le aplicați în, să spunem, un anumit model de afaceri, poate cauza probleme.
Una dintre problemele majore cauzate de multicoliniaritate este că aceasta duce la interpretări incorecte și oferă perspective greșite. Coeficienții de regresie liniară sugerează modificarea medie a valorii țintă dacă o caracteristică este modificată cu o unitate. Deci, dacă există multicoliniaritate, acest lucru nu este valabil, deoarece schimbarea unei caracteristici va duce la modificări ale variabilei corelate și modificări ulterioare ale variabilei țintă. Acest lucru duce la perspective greșite și poate produce rezultate periculoase pentru o afacere.
O modalitate foarte eficientă de a trata multicoliniaritatea este utilizarea VIF (Variance Inflation Factor). Cu cât valoarea VIF pentru o caracteristică este mai mare, această caracteristică este mai corelată liniar. Pur și simplu eliminați caracteristica cu o valoare VIF foarte mare și antrenați din nou modelul pe setul de date rămas.
10. Care este forma normală (ecuația) a regresiei liniare? Când ar trebui să fie preferată metodei de coborâre în gradient?
Ecuația normală pentru regresia liniară este -
p=( XTX ) -1 . X T Y
Aici, Y=β T X este modelul pentru regresia liniară,
Y este variabila țintă sau dependentă,
β este vectorul coeficientului de regresie, la care se ajunge folosind ecuația normală,
X este matricea de caracteristici care conține toate caracteristicile sub formă de coloane.
Rețineți aici că prima coloană din matricea X constă din toate cele 1. Aceasta este pentru a încorpora valoarea offset-ului pentru linia de regresie.
Comparație între coborârea gradientului și ecuația normală:
| Coborâre în gradient | Ecuația normală |
| Necesită reglare hiper-parametru pentru alfa (parametru de învățare) | Nici o astfel de nevoie |
| Este un proces iterativ | Este un proces non-iterativ |
| O(kn 2 ) complexitate în timp | O(n 3 ) complexitate în timp datorită evaluării X T X |
| De preferat când n este extrem de mare | Devine destul de lent pentru valori mari ale lui n |
Aici, „ k ” este numărul maxim de iterații pentru coborârea gradientului, iar „ n ” este numărul total de puncte de date din setul de antrenament.
În mod clar, dacă avem date mari de antrenament, ecuația normală nu este preferată pentru utilizare. Pentru valori mici ale lui „ n ”, ecuația normală este mai rapidă decât coborârea gradientului.
Ce este învățarea automată și de ce contează
11. Îți rulezi regresia pe diferite subseturi de date și, în fiecare subset, valoarea beta pentru o anumită variabilă variază foarte mult. Care ar putea fi problema aici?
Acest caz implică faptul că setul de date este eterogen. Deci, pentru a depăși această problemă, setul de date ar trebui grupat în diferite subseturi și apoi modele separate ar trebui construite pentru fiecare cluster. O altă modalitate de a rezolva această problemă este utilizarea modelelor neparametrice, cum ar fi arbori de decizie, care pot trata datele eterogene destul de eficient.

12. Regresia dumneavoastră liniară nu rulează și comunică că există un număr infinit de cele mai bune estimări pentru coeficienții de regresie. Ce ar putea fi în neregulă?
Această condiție apare atunci când există o corelație perfectă (pozitivă sau negativă) între unele variabile. În acest caz, nu există o valoare unică pentru coeficienți și, prin urmare, apare condiția dată.
13. Ce înțelegi prin R 2 ajustat ? Cum este diferit de R2 ?
R2 ajustat , la fel ca R2 , este un reprezentant al numărului de puncte situate în jurul dreptei de regresie. Adică, arată cât de bine se potrivește modelul cu datele de antrenament. Formula pentru R 2 ajustat este -
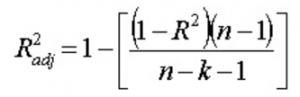
Aici, n este numărul de puncte de date și k este numărul de caracteristici.
Un dezavantaj al lui R2 este că va crește întotdeauna odată cu adăugarea unei noi caracteristici, indiferent dacă noua caracteristică este utilă sau nu. R 2 ajustat depășește acest dezavantaj. Valoarea R 2 ajustată crește numai dacă caracteristica nou adăugată joacă un rol semnificativ în model.
14. Cum interpretați curba valorii reziduale vs ajustate?
Graficul valorii reziduale vs ajustate este utilizat pentru a vedea dacă valorile prezise și reziduurile au sau nu o corelație. Dacă reziduurile sunt distribuite normal, cu o medie în jurul valorii ajustate și o varianță constantă, modelul nostru funcționează bine; în caz contrar, există o problemă cu modelul.
Cea mai frecventă problemă care poate fi întâlnită la antrenamentul modelului pe o gamă largă de un set de date este heteroscedasticitatea (acest lucru este explicat în răspunsul de mai jos). Prezența heteroscedasticității poate fi observată cu ușurință prin reprezentarea grafică a curbei valorii reziduale vs ajustate.
15. Ce este heteroscedasticitatea? Care sunt consecințele și cum le puteți depăși?
Se spune că o variabilă aleatorie este heteroscedastică atunci când diferite subpopulații au variabilități diferite (deviația standard).
Existența heteroscedasticității dă naștere la anumite probleme în analiza regresiei, deoarece ipoteza spune că termenii de eroare sunt necorelați și, prin urmare, varianța este constantă. Prezența heteroscedasticității poate fi adesea observată sub forma unui grafic de împrăștiere în formă de con pentru valorile reziduale vs ajustate.
Una dintre ipotezele de bază ale regresiei liniare este că heteroscedasticitatea nu este prezentă în date. Datorită încălcării ipotezelor, estimatorii MCO (Ordinary Least Squares) nu sunt cei mai buni estimatori liniari imparțiali (ALBASTRU). Prin urmare, ei nu oferă cea mai mică varianță decât alți estimatori liniari imparțiali (LUE).
Nu există o procedură fixă pentru a depăși heteroscedasticitatea. Cu toate acestea, există câteva moduri care pot duce la o reducere a heteroscedasticității. Sunt -
- Logaritmizarea datelor: o serie care crește exponențial are ca rezultat adesea o variabilitate crescută. Acest lucru poate fi depășit folosind transformarea jurnalului.
- Folosind regresia liniară ponderată: Aici, metoda MCO este aplicată valorilor ponderate ale lui X și Y. O modalitate este de a atașa ponderi direct legate de mărimea variabilei dependente.
16. Ce este VIF? Cum o calculezi?
Variance Inflation Factor (VIF) este utilizat pentru a verifica prezența multicolinearității într-un set de date. Se calculează ca:
Aici, VIF j este valoarea lui VIF pentru j- a variabilă,
Rj 2 este valoarea R 2 a modelului atunci când acea variabilă este regresată față de toate celelalte variabile independente.
Dacă valoarea VIF este mare pentru o variabilă, înseamnă că R 2 valoarea modelului corespunzător este mare, adică alte variabile independente sunt capabile să explice acea variabilă. În termeni simpli, variabila este dependentă liniar de alte variabile.
17. De unde știți că regresia liniară este potrivită pentru orice date date?
Pentru a vedea dacă regresia liniară este potrivită pentru orice date date, poate fi utilizat un grafic de dispersie. Dacă relația pare liniară, putem alege un model liniar. Dar dacă nu este cazul, trebuie să aplicăm câteva transformări pentru a face relația liniară. Trasarea graficelor de dispersie este ușoară în cazul regresiei liniare simple sau univariate. Dar în cazul regresiei liniare multivariate, pot fi reprezentate diagrame de dispersie bidimensionale, diagrame rotative și grafice dinamice.
18. Cum se utilizează testarea ipotezelor în regresia liniară?
Testarea ipotezelor poate fi efectuată în regresie liniară în următoarele scopuri:
- Pentru a verifica dacă un predictor este semnificativ pentru predicția variabilei țintă. Două metode comune pentru aceasta sunt:
- Prin utilizarea valorilor p:
Dacă valoarea p a unei variabile este mai mare decât o anumită limită (de obicei 0,05), variabila este nesemnificativă în predicția variabilei țintă. - Prin verificarea valorilor coeficientului de regresie:
Dacă valoarea coeficientului de regresie corespunzător unui predictor este zero, acea variabilă este nesemnificativă în predicția variabilei țintă și nu are nicio relație liniară cu aceasta.
- Prin utilizarea valorilor p:
- Pentru a verifica dacă coeficienții de regresie calculați sunt buni estimatori ai coeficienților reali.
19. Explicați coborârea gradientului în raport cu regresia liniară.
Coborârea gradientului este un algoritm de optimizare. În regresia liniară, este utilizat pentru a optimiza funcția de cost și pentru a găsi valorile βs (estimatorilor) corespunzătoare valorii optimizate a funcției de cost.
Coborârea în gradient funcționează ca o minge care se rostogolește pe un grafic (ignorând inerția). Mingea se mișcă de-a lungul direcției celui mai mare gradient și se odihnește la suprafața plană (minim). 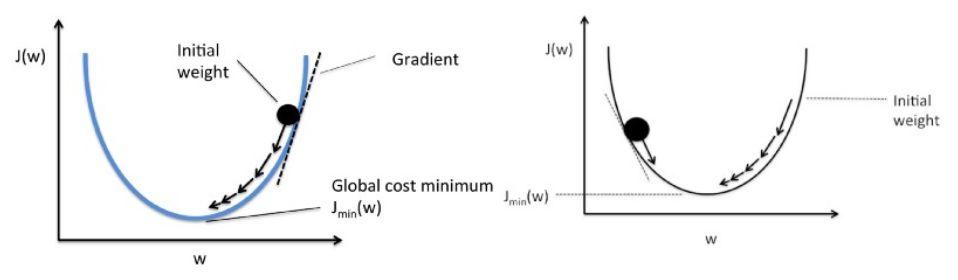
Din punct de vedere matematic, scopul coborârii gradientului pentru regresia liniară este de a găsi soluția
ArgMin J(Θ 0 ,Θ 1 ), unde J(Θ 0 ,Θ 1 ) este funcția de cost a regresiei liniare. Este dat de - 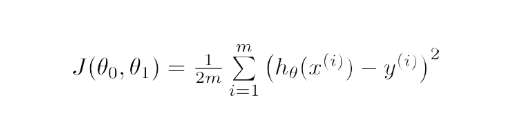
Aici, h este modelul de ipoteză liniară, h=Θ 0 + Θ 1 x, y este rezultatul adevărat și m este numărul punctelor de date din setul de antrenament.
Gradient Descent începe cu o soluție aleatorie, iar apoi pe baza direcției gradientului, soluția este actualizată la noua valoare în care funcția de cost are o valoare mai mică.
Actualizarea este:
Repetați până la convergență 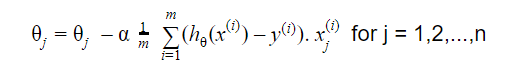
20. Cum interpretați un model de regresie liniară?
Un model de regresie liniară este destul de ușor de interpretat. Modelul are următoarea formă: 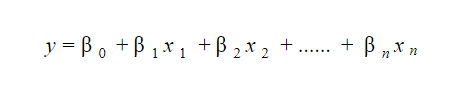
Semnificația acestui model constă în faptul că se pot interpreta și înțelege cu ușurință schimbările marginale și consecințele acestora. De exemplu, dacă valoarea lui x 0 crește cu 1 unitate, păstrând alte variabile constante, creșterea totală a valorii lui y va fi β i . Matematic, termenul de interceptare ( β 0 ) este răspunsul când toți termenii predictori sunt setați la zero sau nu sunt luați în considerare.
Aceste 6 tehnici de învățare automată îmbunătățesc asistența medicală
21. Ce este regresia robustă?
Un model de regresie ar trebui să fie de natură robustă. Aceasta înseamnă că, cu modificări în câteva observații, modelul nu ar trebui să se schimbe drastic. De asemenea, nu ar trebui să fie foarte afectat de valori aberante.
Un model de regresie cu MOL (Meleciume Pătrate Ordinare) este destul de sensibil la valori aberante. Pentru a depăși această problemă, putem folosi metoda WLS (Weighted Least Squares) pentru a determina estimatorii coeficienților de regresie. Aici, se acordă mai puține greutăți valorii aberante sau punctelor de pârghie ridicate din fiting, făcând aceste puncte mai puțin impactante.
22. Ce grafice se sugerează să fie respectate înainte de montarea modelului?
Înainte de a ajusta modelul, trebuie să fiți bine conștienți de date, cum ar fi care sunt tendințele, distribuția, asimetria etc. în variabile. Grafice precum histogramele, diagramele cu case și diagramele cu puncte pot fi utilizate pentru a observa distribuția variabilelor. În afară de aceasta, trebuie să se analizeze și care este relația dintre variabilele dependente și cele independente. Acest lucru se poate face prin diagrame de dispersie (în cazul problemelor univariate), diagrame rotative, diagrame dinamice etc.
23. Ce este modelul liniar generalizat?
Modelul liniar generalizat este derivata modelului de regresie liniară obișnuită. GLM este mai flexibil în ceea ce privește reziduurile și poate fi utilizat acolo unde regresia liniară nu pare adecvată. GLM permite ca distribuția reziduurilor să fie diferită de o distribuție normală. Generalizează regresia liniară permițând modelului liniar să se conecteze la variabila țintă folosind funcția de legătură. Estimarea modelului se face folosind metoda estimării cu maximă probabilitate.
24. Explicați compromisul de părtinire-varianță.
Bias se referă la diferența dintre valorile prezise de model și valorile reale. Este o eroare. Unul dintre scopurile unui algoritm ML este să aibă o părtinire scăzută.
Varianta se referă la sensibilitatea modelului la mici fluctuații ale setului de date de antrenament. Un alt obiectiv al unui algoritm ML este acela de a avea o varianță scăzută.
Pentru un set de date care nu este tocmai liniar, nu este posibil să fie atât prejudecata, cât și varianța scăzute în același timp. Un model în linie dreaptă va avea varianță scăzută, dar părtinire mare, în timp ce un polinom de grad înalt va avea părtinire scăzută, dar varianță mare.
Nu există nicio scăpare de relația dintre părtinire și variație în învățarea automată.
- Scăderea părtinirii crește varianța.
- Scăderea varianței crește părtinirea.
Deci, există un compromis între cele două; specialistul ML trebuie să decidă, pe baza problemei atribuite, cât de multă părtinire și varianță poate fi tolerată. Pe baza acestuia se construiește modelul final.
25. Cum pot curbele de învățare să contribuie la crearea unui model mai bun?
Curbele de învățare indică prezența supraajustării sau subajustării.
Într-o curbă de învățare, eroarea de antrenament și eroarea de validare încrucișată sunt reprezentate grafic în funcție de numărul de puncte de date de antrenament. O curbă tipică de învățare arată astfel: 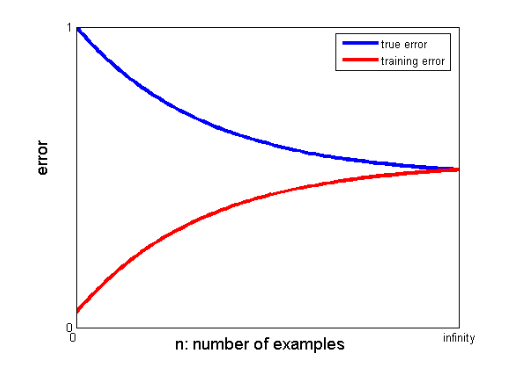
Dacă eroarea de antrenament și eroarea adevărată (eroarea de validare încrucișată) converg către aceeași valoare și valoarea corespunzătoare a erorii este mare, aceasta indică faptul că modelul nu se potrivește și suferă de părtinire mare.
Interviuri de învățare automată și cum să le obțineți
Interviurile de învățare automată pot varia în funcție de tipuri sau categorii, de exemplu, câțiva recrutori pun multe întrebări la interviu cu regresia liniară . Atunci când optează pentru interviul de inginer de învățare automată, se pot specializa în categorii precum codificare, cercetare, studiu de caz, management de proiect, prezentare, proiectare de sistem și statistici. Ne vom concentra pe cele mai comune tipuri de categorii și pe cum să ne pregătim pentru ele.
- Codificare
Codarea și programarea sunt componente importante ale unui interviu de învățare automată și sunt frecvent utilizate pentru a selecta candidații. Pentru a te descurca bine în aceste interviuri, trebuie să ai abilități solide de programare. Interviurile de codificare durează de obicei între 45 și 60 de minute și sunt compuse din doar două întrebări. Intervievatorul pune subiectul și anticipează că solicitantul îl va aborda în cel mai mic timp posibil.
Cum să vă pregătiți – Vă puteți pregăti pentru aceste interviuri având o bună înțelegere a structurilor datelor, a complexității timpului și spațiului, a abilităților de management și a capacității de a înțelege și rezolva o problemă. upGrad are un curs grozav de inginerie software care vă poate ajuta să vă îmbunătățiți abilitățile de codificare și să obțineți acel interviu.
2. Învățare automată
Înțelegerea dvs. despre învățarea automată va fi evaluată prin interviuri. Straturile convoluționale, rețelele neuronale recurente, rețelele adversare generative, recunoașterea vorbirii și alte subiecte pot fi acoperite în funcție de nevoile de angajare.
Cum să te pregătești – Pentru a putea susține acest interviu, trebuie să te asiguri că ai o înțelegere aprofundată a rolurilor și responsabilităților postului. Acest lucru vă va ajuta să identificați specificațiile ML pe care trebuie să le studiați. Cu toate acestea, dacă nu întâlniți nicio specificație, trebuie să înțelegeți profund elementele de bază. Un curs aprofundat de ML oferit de upGrad vă poate ajuta în acest sens. De asemenea, puteți studia cele mai recente articole despre ML și AI pentru a înțelege cele mai recente tendințe ale acestora și le puteți încorpora în mod regulat.
3. Screening
Acest interviu este oarecum informal și de obicei unul dintre punctele inițiale ale interviului. Un potențial angajator se ocupă adesea de asta. Scopul principal al acestui interviu este de a oferi solicitantului un simț al afacerii, al rolului și al îndatoririlor. Într-o atmosferă mai informală, candidatul este, de asemenea, chestionat despre trecutul său pentru a determina dacă domeniul său de interes se potrivește cu poziția.
Cum să vă pregătiți – Aceasta este o parte foarte netehnică a interviului. Tot ceea ce este necesar este onestitatea dvs. și elementele de bază ale specializării dvs. în Machine Learning.
4. Proiectarea sistemului
Astfel de interviuri testează capacitatea unei persoane de a crea o soluție complet scalabilă de la început până la sfârșit. Majoritatea inginerilor sunt atât de preocupați de o problemă, încât adesea trec cu vederea imaginea generală. Un interviu de proiectare a sistemului necesită înțelegerea numeroaselor elemente care se combină pentru a produce o soluție. Aceste elemente includ aspectul front-end, echilibrul de încărcare, memoria cache și multe altele. Un sistem end-to-end eficient și scalabil este mai ușor de dezvoltat atunci când aceste probleme sunt bine înțelese.
Cum să vă pregătiți – Înțelegeți conceptele și componentele proiectului de proiectare a sistemului. Folosiți exemple din viața reală pentru a explica structura intervievatorului pentru o mai bună înțelegere a proiectului.
Bloguri populare de învățare automată și inteligență artificială
| IoT: istorie, prezent și viitor | Tutorial de învățare automată: Învățați ML | Ce este algoritmul? Simplu și Ușor |
| Salariu inginer robotic în India: toate rolurile | O zi din viața unui inginer de învățare automată: ce fac ei? | Ce este IoT (Internet of Things) |
| Permutare vs combinație: diferența dintre permutare și combinație | Top 7 tendințe în inteligența artificială și învățarea automată | Învățare automată cu R: tot ce trebuie să știți |

Dacă există un decalaj semnificativ între valorile convergente ale erorilor de antrenament și de validare încrucișată, adică eroarea de validare încrucișată este semnificativ mai mare decât eroarea de antrenament, sugerează că modelul se adaptează prea mult la datele de antrenament și suferă de o varianță mare. .
Ingineri de învățare automată: mituri vs. realități
Acesta este sfârșitul primei secțiuni a acestei serii. Rămâneți pentru următoarea parte a seriei, care constă în întrebări bazate pe regresia logistică . Simțiți-vă liber să postați comentariile dvs.
Coautor: Ojas Agarwal
Puteți verifica programul nostru Executive PG în Machine Learning și AI , care oferă ateliere practice practice, mentor individual în industrie, 12 studii de caz și sarcini, statutul de absolvenți IIIT-B și multe altele.
Ce intelegi prin regularizare?
Regularizarea este o strategie de abordare a problemei supraadaptării modelului. Supraadaptarea apare atunci când un model complicat este aplicat datelor de antrenament. Modelul de bază poate să nu poată generaliza datele uneori, iar modelul complicat poate supraadapta datele. Regularizarea este folosită pentru a atenua această problemă. Regularizarea este procesul de adăugare a termenilor de coeficienți (beta) la problema minimizării în așa fel încât termenii să fie penalizați și să aibă o amploare modestă. Acest lucru ajută, în esență, la identificarea tiparelor de date, prevenind, de asemenea, supraadaptarea, împiedicând modelul să devină prea complex.
Ce înțelegeți despre ingineria caracteristicilor?
Procesul de schimbare a datelor originale în caracteristici care descriu mai bine problema de bază în modele predictive, rezultând o precizie îmbunătățită a modelului pe date nevăzute, este cunoscut sub numele de inginerie de caracteristici. În termeni simpli, ingineria caracteristicilor se referă la crearea de caracteristici suplimentare care pot ajuta la o mai bună înțelegere și modelare a unei probleme. Există două tipuri de inginerie a caracteristicilor: bazată pe afaceri și bazată pe date. Încorporarea de caracteristici din punct de vedere comercial este punctul central al ingineriei caracteristicilor bazate pe afaceri.
Care este compromisul bias-varianță?
Diferența dintre modelul - valorile prezise și valorile reale este denumită părtinire. E o greseala. O părtinire scăzută este unul dintre obiectivele unui algoritm ML. Vulnerabilitatea modelului la mici modificări ale setului de date de antrenament este denumită varianță. Varianta scăzută este un alt obiectiv al unui algoritm ML. Este imposibil să existe atât părtinire scăzută, cât și varianță scăzută într-un set de date care nu este perfect liniar. Varianța unui model în linie dreaptă este scăzută, dar părtinirea este mare, în timp ce varianța unui polinom de grad înalt este scăzută, dar părtinirea este mare. În învățarea automată, legătura dintre părtinire și variație este inevitabilă.
