Introducere în funcția de densitate de probabilitate [formule, proprietăți, aplicații, exemple]

Funcția de densitate a probabilității (PDF) este o expresie în statistică care denotă distribuția probabilității unei variabile aleatoare discrete. Distribuția probabilității, în termeni simpli, poate fi definită ca o probabilitate a unui rezultat al unei variabile aleatorii, cum ar fi o acțiune sau un ETF. Variabilele discrete apar în contrast cu o variabilă aleatoare continuă a cărei valoare exactă poate fi determinată.

De exemplu, valoarea scrip într-o piață de valori are doar două zecimale (de exemplu, 65,76) într-o variabilă aleatorie discretă în loc de o variabilă continuă cu orice număr de zecimale (de exemplu: 65,7685434567).

O funcție de densitate de probabilitate este un instrument statistic utilizat pentru a determina probabilitatea rezultatului unei variabile aleatoare discrete. Când sunt reprezentate pe un grafic, PDF-urile arată identic cu o curbă clopot în care aria de sub curbă reprezintă probabilitatea rezultatului.

Atunci când este proiectată ca model grafic, aria de sub curbă reprezintă intervalul în care vor cădea valorile variabilelor aleatoare discrete. Astfel, aria totală sub curbă este egală cu probabilitatea rezultatului variabilei.

Funcția de densitate de probabilitate poate determina probabilitatea ca o variabilă aleatoare să se încadreze într-un interval specific de valori.

De obicei, funcțiile de densitate de probabilitate analizează riscurile și veniturile potențiale asociate cu un anumit fond de pe piața de valori.

Condițiile care trebuie îndeplinite de o funcție să fie considerată o funcție de densitate de probabilitate

Valoarea unei variabile discrete poate fi măsurată cu precizie în contrast cu o variabilă continuă care poate avea un număr infinit de valori. Orice funcție ar trebui să îndeplinească următoarele două condiții pentru a fi o funcție de densitate de probabilitate:

• Valoarea f(x) pentru fiecare valoare posibilă a variabilei aleatoare ar trebui să fie pozitivă (nenegativă).
• Valoarea integrală a ariei totale a curbei (integrala tuturor valorilor posibile ale variabilei aleatoare) ar trebui să fie 1.

Diferența dintre funcția de densitate a probabilității și funcția de distribuție a probabilității

Variabilele aleatoare pot avea multe valori. Descrierea fiecărei valori posibile pe care o poate avea o variabilă aleatoare se numește distribuția ei de probabilitate.

Distribuția probabilității oferă un set de rezultate și probabilitățile aferente acestora. Funcția statistică care reprezintă o distribuție continuă de probabilitate este cunoscută sub denumirea de funcție de densitate a probabilității.

Există un alt instrument statistic care reprezintă o distribuție de probabilitate discretă numită funcție de masă a probabilității. Aceasta oferă o descriere detaliată a tuturor rezultatelor posibile și a probabilităților lor.

Expresia pentru funcțiile de densitate de probabilitate

Dacă variabila aleatoare este discretă, distribuția ei de probabilitate se numește funcție de masă de probabilitate, iar dacă este o variabilă continuă, distribuția de probabilitate se numește funcție de densitate de probabilitate.

Un PDF este utilizat atunci când variabila aleatoare în cauză are o gamă de valori posibile. Distribuția lor de probabilitate este utilizată pentru a determina valoarea exactă.

Fie ca variabila aleatoare să fie notată cu X. Funcția de densitate de probabilitate, f a variabilei aleatoare X poate fi exprimată ca

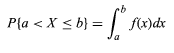
• Valoarea variabilei aleatoare se află între a și b.
• Dacă X denotă probabilitatea de a selecta un anumit număr din intervalul (intervalul) r și s, atunci funcția de densitate a probabilității poate fi exprimată ca

f ( x ) = 1/( s − r ) pentru r < x < s și f ( x ) = 0 pentru x < r sau x > s .

• PDF F este reprezentat ca:

F ( x ) = P { X ≤ x }

care se numește funcția de distribuție sau funcția de distribuție cumulativă a lui X.

Considerând că variabila aleatoare X are o funcție de distribuție a probabilității f ( x ), atunci relația dintre f și F poate fi stabilită ca

F ′(. x ) = f ( x )

Funcția de distribuție a unei variabile aleatoare discrete este diferită de funcția de distribuție a probabilității. Relația dintre cele două poate fi exprimată astfel:

Așteptările variabilei aleatoare se notează ca:

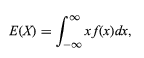
Astfel, toate variabilele discrete și aleatorii pot fi tratate uniform cu ajutorul unei teorii combinate.

Formula funcției de densitate de probabilitate

Probabilitatea unei variabile aleatoare continue X pe o valoare fixă ​​x este întotdeauna 0. În acest caz, P(X = x) nu poate fi utilizat. Valoarea lui X situată între un interval de valori (a,b) trebuie determinată. Pentru a determina același lucru, se folosește următoarea formulă.

Proprietățile unei funcții de densitate de probabilitate

O variabilă aleatoare continuă care își ia valoarea între intervalul (a,b), de exemplu, va fi estimată prin calcularea ariei de sub curbă și a axei X reprezentată grafic cu (a) ca limită inferioară și (b) ca limită inferioară. Limita superioară. Funcția de densitate de probabilitate pentru cele de mai sus este reprezentată ca:

Funcția de densitate de probabilitate este pozitivă (nenegativă) pentru toate valorile posibile. Aceasta înseamnă f(x)≥ 0, pentru fiecare x. Aria care se încadrează între curba de densitate și axa X (axa orizontală) este egală cu 1.

Acesta poate fi de asemenea notat ca:

Curba funcției de densitate este continuă în intervalul dat, care este clar definită față de o serie de valori continue sau domeniul variabilei.

Alăturați-vă Cursului de învățare automată online de la cele mai bune universități din lume – Master, Programe Executive Postuniversitare și Program de Certificat Avansat în ML și AI pentru a vă accelera cariera.

Aplicații ale funcției de densitate de probabilitate

• Funcția de densitate de probabilitate este utilizată în modelarea anuală a nivelurilor de concentrație de NO din atmosferă.
• Modelarea arderii motoarelor diesel.
• În statistică, funcția de densitate de probabilitate este utilizată pentru a determina posibilitățile rezultatului unei variabile aleatoare.

Exemple de funcție de densitate de probabilitate

• Exemplul 1

Mai jos este un exemplu despre modul în care funcția de densitate a probabilității (PDF) este utilizată pentru a determina potențialul de risc al unui investitor pe piața de valori:

În primul rând, PDF-urile sunt generate ca instrument grafic bazat pe informații istorice.

Cea mai comună formă de PDF este proiecția neutră, unde riscul este egal cu recompensa într-o gamă largă de posibilități. Investitorii cu o capacitate mai mică de asumare a riscurilor vor fi răsplătiți doar cu profituri limitate și, prin urmare, se află sub partea stângă a curbei clopot. În schimb, investitorii cu abilități mari de asumare a riscurilor sunt susceptibili de a fi recompensați cu randamente mai mari și, prin urmare, să se încadreze în partea dreaptă a curbei.

Majoritatea investitorilor se încadrează în capacitatea medie de asumare a riscurilor și, prin urmare, ocupă mijlocul curbei.

Acest lucru ajută la analiza categoriei de investitori pe baza datelor primite. Acest lucru îi ajută pe brokerii bursieri să-și identifice categoria țintă de clienți pentru a-și vinde produsele.

• Exemplul 2

Una dintre aplicațiile esențiale ale funcției de densitate de probabilitate este variabila aleatoare gaussiană, cunoscută și ca variabilă aleatoare normală.

În ambele cazuri, graficul oferă o curbă clopot pentru funcția de densitate de probabilitate.

Densitatea poate fi exprimată ca

Graficul ecuației densității de mai sus este prezentat mai jos.

Aria de sub curbă reprezintă valoarea reală a variabilei aleatoare gaussiene.

Concluzie

Funcția de densitate a probabilității joacă un rol vital în învățarea automată. Pentru studenții care doresc o carieră în învățarea automată și inteligența artificială, recomandăm cu căldură să se înscrie la programul de certificat avansat IIT de la upGrad în învățarea automată . Programul este personalizat și conceput pentru a echipa profesioniști seniori care lucrează să implementeze modele de învățare automată folosind tehnologia cloud computing.

Curriculumul este conceput de profesori de la IIT Madras și experți din industrie pentru a face procesul de învățare mai relevant și mai practic. Programul oferă certificare recunoscută la nivel global de la râvnitul și clasat pe locul 1 colegiu de inginerie din India și sprijin de plasare de 360 ​​de grade de la upGrad.

În plus, aveți numeroase oportunități de a colabora la proiecte de anvergură cu baza de cursanți plătiți de la upGrad de peste 40.000 de persoane.

Accesați site-ul nostru pentru a începe călătoria dvs. de învățare!