Introducere în regresia multivariată în învățarea automată: Ghid complet

Nu este un secret pentru nimeni că tehnologia actuală este bazată pe date. Datele pot fi doar o compilație de cifre, dar pot fi procesate în mod semnificativ pentru a extrage productivitate și ingeniozitate pentru ca întreprinderile să rămână competitive și sustenabile pe termen lung. După cum se întâmplă, analiza datelor este răspunsul pentru a obține estimări precise din informații brute.

Analiza datelor este o tehnică care implică idei statistice și logice pentru a analiza, procesa și transforma datele într-o formă utilizabilă. Soluțiile care sunt trase prin analiza datelor sunt folosite în afaceri pentru a lua decizii vitale. Știința datelor împreună cu analiza datelor sunt utilizate pentru a prezice rezultatele viitoare cu o acuratețe ridicată. Este un proces de utilizare a tehnicilor științifice și a algoritmilor pentru a obține informații viabile dintr-un grup de date.

O problemă comună cu care se confruntă profesioniștii în date este modul în care se stabilește dacă există o relație statistică între o variabilă de răspuns (notată cu Y) și variabilele explicative (notate cu Xi).

Răspunsul la această îngrijorare este analiza de regresie. Să înțelegem acest lucru în detaliu.

Ce este analiza de regresie?

Analiza regresiei este una dintre metodele populare în analiza datelor care urmează un algoritm de învățare automată controlat sau supravegheat. Este o tehnică eficientă pentru a identifica și a stabili o relație între variabilele din date.

Analiza de regresie implică sortarea variabilelor viabile folosind strategii matematice pentru a trage concluzii foarte precise despre acele variabile sortate.

Ce este regresia multivariată?

Multivariate este un algoritm de învățare automată controlat sau supravegheat care analizează mai multe variabile de date. Este o continuare a regresiei multiple care implică o variabilă dependentă și multe variabile independente. Rezultatul este prezis pe baza numărului de variabile independente.

Regresia multivariată determină o formulă care explică răspunsul simultan al factorilor prezenți în variabile la modificările altora. Sunt folosite pentru a studia datele în diverse domenii. De exemplu, regresia multivariată în imobiliare este utilizată pentru a prezice prețul unei case pe baza mai multor factori, cum ar fi locația acesteia, numărul de camere și facilitățile disponibile.

Funcția de cost în regresia multivariată

Funcția de cost alocă un cost eșantioanelor atunci când rezultatul unui model se abate de la datele observate. Ecuația funcției de cost este totalul pătratului diferenței dintre valoarea prezisă și valoarea reală împărțit la de două ori lungimea setului de date.

Iată un exemplu :

rezultat :

Sursă

Cum se utilizează analiza de regresie multivariată?

Procesele implicate în analiza de regresie multivariată includ selecția caracteristicilor, proiectarea caracteristicilor, normalizarea caracteristicilor, funcțiile de pierdere a selecției, analiza ipotezelor și crearea unui model de regresie.

1. Selectarea caracteristicilor: Este cel mai important pas în regresia multivariată. Cunoscut și sub denumirea de selecție a variabilelor, acest proces implică selectarea variabilelor viabile pentru a construi modele eficiente.
2. Normalizarea caracteristicilor: Aceasta implică scalarea caracteristicilor pentru a menține distribuția eficientă și rapoartele de date. Acest lucru ajută la o mai bună analiză a datelor. Valoarea tuturor caracteristicilor poate fi modificată în funcție de cerință.
3. Selectarea funcției de pierdere și a ipotezei : Funcția de pierdere este utilizată pentru prezicerea erorilor. Funcția de pierdere intră în joc atunci când predicția ipotezei se schimbă față de cifrele reale. Aici, ipoteza reprezintă valoarea prezisă din caracteristică sau variabilă.
4. Parametrul ipotezei de fixare : Parametrul ipotezei este fixat sau setat astfel încât să minimizeze funcția de pierdere și să îmbunătățească o predicție mai bună.
5. Reducerea funcției de pierdere : Funcția de pierdere este minimizată prin generarea unui algoritm specific pentru minimizarea pierderilor pe setul de date care, la rândul său, facilitează modificarea parametrilor ipotezei. Coborârea gradientului este algoritmul cel mai frecvent utilizat pentru minimizarea pierderilor. Algoritmul poate fi folosit și pentru alte acțiuni odată ce minimizarea pierderilor este completă.
6. Analiza funcției de ipoteză : Funcția ipotezei trebuie analizată deoarece este crucială pentru prezicerea valorilor. După ce funcția este analizată, aceasta este apoi testată pe datele de testare.

Să ne uităm acum la cele două moduri în care poate fi utilizată regresia multivariată.

1. Regresie liniară multivariată

Regresia liniară multivariată seamănă cu regresia liniară simplă, cu excepția faptului că, în regresia liniară multivariată, mai multe variabile independente contribuie la variabilele dependente și astfel se folosesc mai mulți coeficienți în calcul.

• Este folosit pentru a deriva o relație matematică între mai multe variabile aleatoare. Acesta explică câte variabile independente multiple sunt asociate cu o variabilă dependentă.
• Detaliile variabilelor independente multiple sunt utilizate pentru a face o predicție precisă a influenței pe care acestea o au asupra variabilei de rezultat.
• Modelul de regresie liniară multivariată generează o relație într-o formă liniară (o formă de linie dreaptă) cu cea mai bună aproximare a fiecărui punct de date.
• Ecuația modelului de regresie liniară multivariată este:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

unde pentru i=n observații:

Sursă

Când poate fi folosită regresia liniară?

Modelul de regresie liniară poate fi utilizat numai atunci când există două variabile continue dintre care una este dependentă și cealaltă este independentă.

Variabila independentă este folosită ca parametru pentru a determina valoarea sau rezultatul variabilei dependente.

2. Regresie logistică multivariată

Regresia logistică este un algoritm folosit pentru a prezice un rezultat binar bazat pe mai multe variabile independente. Un rezultat binar are două posibilități, fie că se întâmplă scenariul (reprezentat cu 1), fie nu se întâmplă (notat cu 0).

Regresia logistică este utilizată atunci când se lucrează la date binare, datele în care rezultatul (sau variabila dependentă) este dihotomic.

Unde poate fi folosită regresia logistică?

Regresia logistică este folosită în primul rând pentru a trata problemele de clasificare. De exemplu, pentru a stabili dacă un e-mail este spam sau nu și dacă o anumită tranzacție este rău intenționată sau nu. În analiza datelor, este folosit pentru a lua decizii calculate pentru a minimiza pierderile și a crește profiturile.

Regresia logistică multivariată este utilizată atunci când există o variabilă dependentă și rezultate multiple. Diferă de regresia logistică prin faptul că are mai mult de două rezultate posibile.

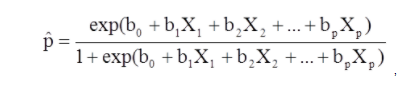
X1 la Xp sunt variabile independente distincte.

b0 la bp sunt coeficienții de regresie

Modelul de regresie logistică multiplă poate fi scris și într-o formă diferită. În formularul de mai jos, rezultatul este jurnalul așteptat al șanselor ca rezultatul să fie prezent,

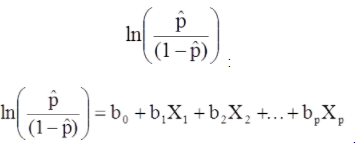
Modelul de regresie logistică multiplă poate fi scris și într-o formă diferită. În formularul de mai jos, rezultatul este jurnalul așteptat al șanselor ca rezultatul să fie prezent.

Partea dreaptă a ecuației de mai sus seamănă cu ecuația de regresie liniară, dar metoda de aflare a coeficienților de regresie diferă.

Ipoteze în modelul de regresie multivariată

• Variabilele dependente și independente au o relație liniară.
• Variabilele independente nu au o corelație puternică între ele.
• Observațiile lui yi sunt alese aleatoriu și individual din populație.

Ipoteze în modelul de regresie logistică multivariată

• Variabila dependentă este nominală sau ordinală. Variabilele nominale au două sau mai multe categorii fără nicio organizare semnificativă. Variabilele ordinale pot avea și două sau mai multe categorii, dar au o structură și pot fi ordonate.
• Pot exista variabile independente simple sau multiple care pot fi ordinale, continue sau nominale. Variabilele continue sunt acelea care pot avea valori infinite într-un interval specific.
• Variabilele dependente se exclud reciproc și sunt exhaustive.
• Variabilele independente nu au o corelație puternică între ele.

Avantajele regresiei multivariate

1. Regresia multivariată ne ajută să studiem relațiile dintre mai multe variabile din setul de date.
2. Corelația dintre variabilele dependente și cele independente ajută la prezicerea rezultatului.
3. Este unul dintre cei mai convenabili și populari algoritmi utilizați în învățarea automată.

Dezavantajele regresiei multivariate

• Complexitatea tehnicilor multivariate necesită calcule matematice complexe.
• Nu este ușor de interpretat rezultatul modelului de regresie multivariată, deoarece există inconsecvențe în rezultatele pierderilor și erorilor.
• Modelele de regresie multivariată nu pot fi aplicate la seturi de date mai mici; sunt concepute pentru a produce rezultate precise atunci când vine vorba de seturi de date mai mari.

Dacă doriți să aflați mai multe despre regresia multivariată și alte subiecte complexe de știință a datelor, upGrad are soluția potrivită pentru dvs. Cursul nostru de master în știința datelor de la Universitatea John Moores din Liverpool, de 18 luni , acoperă peste 500 de ore de învățare riguroase, 25 de sesiuni de coaching (desfășurate pe o bază de 1:8) și peste 20 de sesiuni live. upGrad oferă, de asemenea, asistență didactică 1:1 și asistență de orientare în carieră la 360° pentru ca studenții să își transforme cariera. Cursanții pot valorifica învățarea peer-to-peer pe platforma globală cu peste 40.000 de cursanți plătiți și pot lucra la proiecte de colaborare în șase specializări funcționale pentru a-și maximiza experiența de învățare.