Implementați algoritmul de sortare de numărare în Java

Publicat: 2023-01-30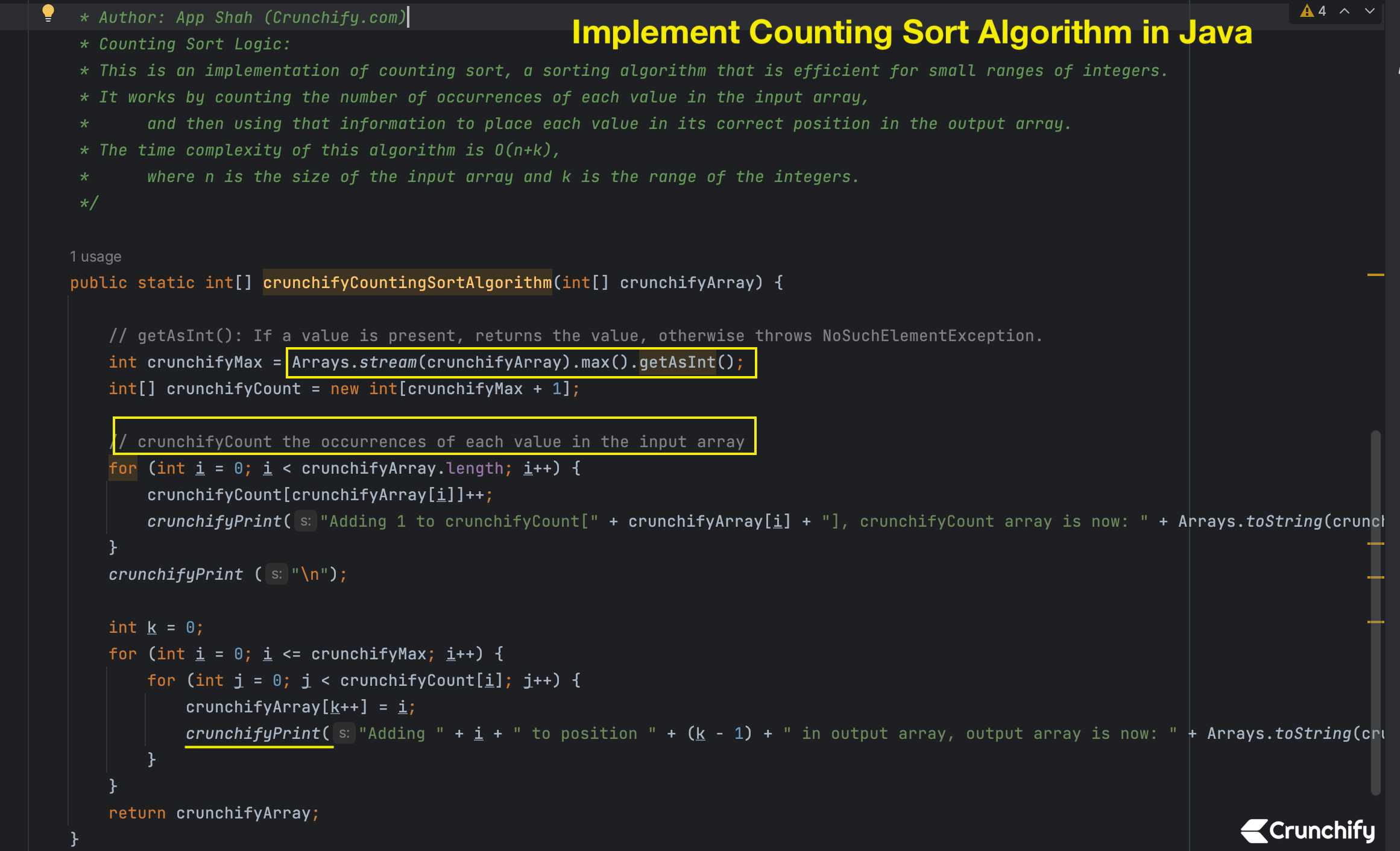
Implementați algoritmul de sortare de numărare în Java

Ce este algoritmul de sortare de numărare?

Counting sort, un algoritm de sortare care este eficient pentru small ranges of integers . Funcționează prin numărarea numărului de apariții ale fiecărei valori în matricea de intrare și apoi folosind acele informații pentru a plasa fiecare valoare în poziția corectă în matricea de ieșire.

Complexitatea de timp a acestui algoritm este O(n+k) , unde n este dimensiunea matricei de intrare și k este intervalul numerelor întregi.

CrunchifyCountingSortAlgo.java

Iată o implementare completă a Counting Sort în Java. Doar copiați-l în IDEA preferată și rulați-l.

 pachet crunchify.com.java.tutorials;

import java.util.Arrays;

/**
 * @autor Crunchify.com
 * Program: Cum se implementează algoritmul de sortare de numărare în java?
 * Counting sort este un algoritm de sortare care sortează elementele unui tablou 
 * prin numărarea numărului de apariții ale fiecărui element unic din matrice.
 */

clasă publică CrunchifyCountingSortAlgo {

    public static void main(String[] args) {

        // Integer Matrice de 10 elemente
        int[] crunchifyArray = {9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3};

        crunchifyPrint("Matrice originală: " + Arrays.toString(crunchifyArray));
        crunchifyPrint ("\n");

        CrunchifyCountingSortAlgo crunchify = nou CrunchifyCountingSortAlgo();
        crunchify.crunchifyCountingSortAlgorithm(crunchifyArray);

        crunchifyPrint ("\n");
        crunchifyPrint("Rezultatul algoritmului de sortare de numărare Crunchify: " + Arrays.toString(crunchifyArray));
    }

    private static void crunchifyPrint(String s) {

        Printlns.out.system(e);
    }


    /**
     * Autor: App Shah (Crunchify.com)
     *
     * Logica de sortare de numărare:
     * Aceasta este o implementare a sortării de numărare, un algoritm de sortare care este eficient pentru intervale mici de numere întregi.
     * Funcționează prin numărarea numărului de apariții ale fiecărei valori din matricea de intrare,
     * și apoi folosind acele informații pentru a plasa fiecare valoare în poziția corectă în matricea de ieșire.
     * Complexitatea temporală a acestui algoritm este O(n+k),
     * unde n este dimensiunea matricei de intrare și k este intervalul numerelor întregi.
     */


    public static int[] crunchifyCountingSortAlgorithm(int[] crunchifyArray) {

        // getAsInt(): Dacă o valoare este prezentă, returnează valoarea, altfel aruncă NoSuchElementException.
        int crunchifyMax = Arrays.stream(crunchifyArray).max().getAsInt();
        int[] crunchifyCount = new int[crunchifyMax + 1];

        // crunchifyCount aparițiile fiecărei valori din tabloul de intrare
        pentru (int i = 0; i < crunchifyArray.length; i++) {
            crunchifyCount[crunchifyArray[i]]++;
            crunchifyPrint("Se adaugă 1 la crunchifyCount[" + crunchifyArray[i] 
                    + "], matricea crunchifyCount este acum: " + Arrays.toString(crunchifyCount));
        }

        crunchifyPrint ("\n");

        int k = 0;
        pentru (int i = 0; i <= crunchifyMax; i++) {
            pentru (int j = 0; j < crunchifyCount[i]; j++) {
                crunchifyArray[k++] = i;
                crunchifyPrint("Adăugarea " + i + " în poziţia " + (k - 1) 
                        + " în tabloul de ieșire, matricea de ieșire este acum: " + Arrays.toString(crunchifyArray));
            }
        }

        returnează crunchifyArray;
    }

}

Doar rulați programul de mai sus ca aplicație Java în IntelliJ IDEA sau Eclipse IDE și veți avea ca rezultat ca mai jos.

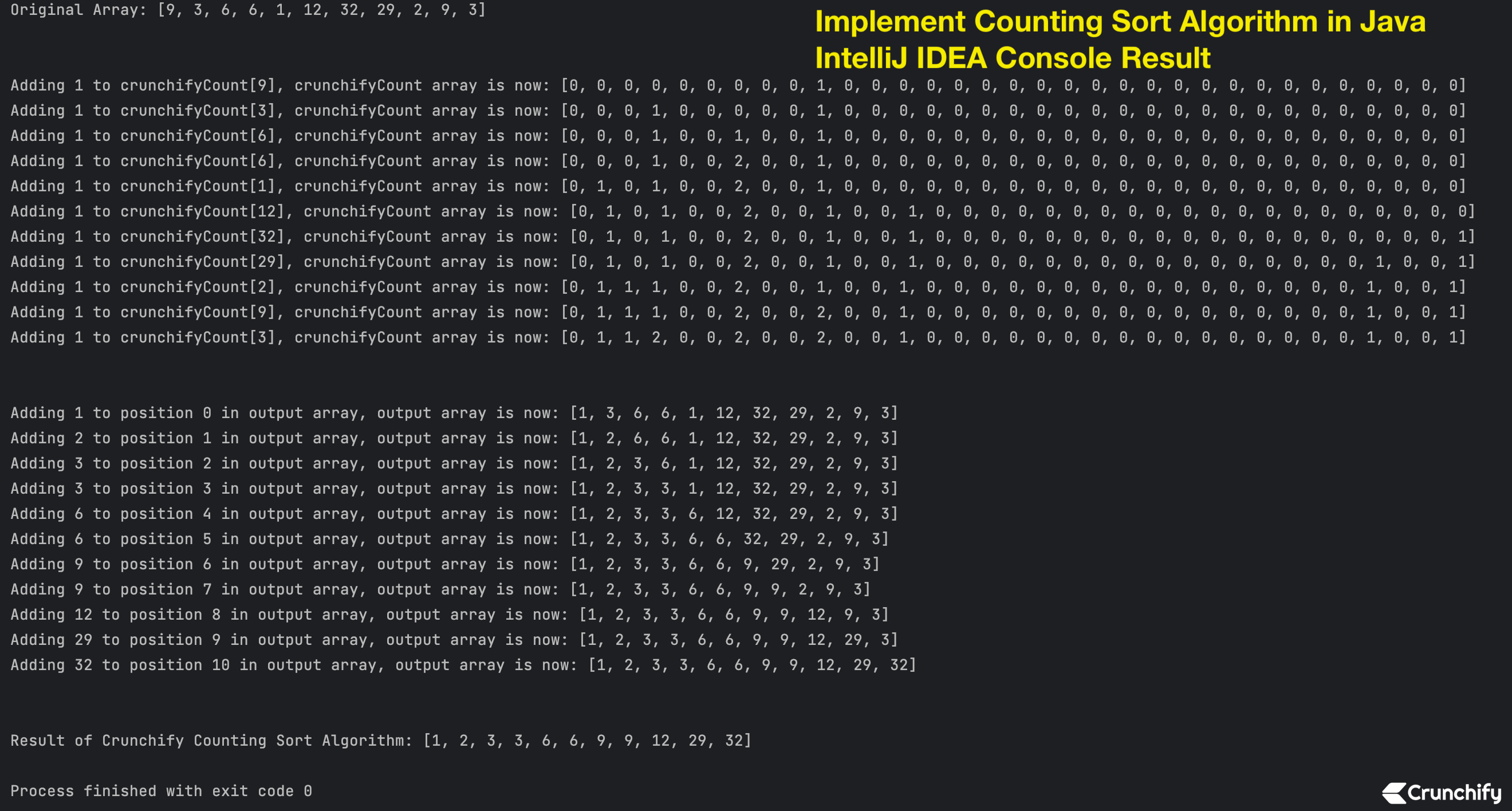
Rezultatul Consolei IntelliJ IDEA

 Matrice originală: [9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3]


Adăugând 1 la crunchifyCount[9], matricea crunchifyCount este acum: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Adăugând 1 la crunchifyCount[3], matricea crunchifyCount este acum: [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Adăugând 1 la crunchifyCount[6], matricea crunchifyCount este acum: [0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Adăugând 1 la crunchifyCount[6], matricea crunchifyCount este acum: [0, 0, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Adăugând 1 la crunchifyCount[1], matricea crunchifyCount este acum: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Adăugând 1 la crunchifyCount[12], matricea crunchifyCount este acum: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Adăugând 1 la crunchifyCount[32], matricea crunchifyCount este acum: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
Adăugând 1 la crunchifyCount[29], matricea crunchifyCount este acum: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
Adăugând 1 la crunchifyCount[2], matricea crunchifyCount este acum: [0, 1, 1, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
Adăugând 1 la crunchifyCount[9], matricea crunchifyCount este acum: [0, 1, 1, 1, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
Adăugând 1 la crunchifyCount[3], matricea crunchifyCount este acum: [0, 1, 1, 2, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]


Adăugând 1 la poziția 0 în matricea de ieșire, matricea de ieșire este acum: [1, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3]
Adăugând 2 la poziția 1 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 6, 6, 1, 12, 32, 29, 2, 9, 3]
Adăugând 3 la poziția 2 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 6, 1, 12, 32, 29, 2, 9, 3]
Adăugând 3 la poziția 3 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 1, 12, 32, 29, 2, 9, 3]
Adăugând 6 la poziția 4 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 6, 12, 32, 29, 2, 9, 3]
Adăugând 6 la poziția 5 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 6, 6, 32, 29, 2, 9, 3]
Adăugând 9 la poziția 6 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 6, 6, 9, 29, 2, 9, 3]
Adăugând 9 la poziția 7 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 6, 6, 9, 9, 2, 9, 3]
Adăugând 12 la poziția 8 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 6, 6, 9, 9, 12, 9, 3]
Adăugând 29 la poziția 9 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 3]
Adăugând 32 la poziția 10 în matricea de ieșire, matricea de ieșire este acum: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32]


Rezultatul algoritmului de sortare de numărare Crunchify: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32]

Procesul s-a încheiat cu codul de ieșire 0
Implementați algoritmul de sortare de numărare în Java - Rezultat IntelliJ IDEA

Anunțați-mă dacă vă confruntați cu vreo problemă de rulare deasupra programului Java Algoritm de sortare de numărare.