Coborâre gradient în învățarea automată: Cum funcționează?

Introducere

Una dintre cele mai importante părți ale Machine Learning este optimizarea algoritmilor săi. Aproape toți algoritmii din Machine Learning au la bază un algoritm de optimizare care acționează ca nucleu al algoritmului. După cum știm cu toții, optimizarea este scopul final al oricărui algoritm, chiar și în cazul evenimentelor din viața reală sau atunci când avem de-a face cu un produs bazat pe tehnologie de pe piață.

În prezent, există o mulțime de algoritmi de optimizare care sunt utilizați în mai multe aplicații, cum ar fi recunoașterea feței, mașinile cu conducere autonomă, analiza bazată pe piață etc. În mod similar, în Machine Learning astfel de algoritmi de optimizare joacă un rol important. Un astfel de algoritm de optimizare utilizat pe scară largă este algoritmul de coborâre a gradientului, pe care îl vom analiza în acest articol.

Ce este Gradient Descent?

În Machine Learning, algoritmul Gradient Descent este unul dintre cei mai folosiți algoritmi și totuși îi uimește pe majoritatea noilor veniți. Din punct de vedere matematic, Gradient Descent este un algoritm de optimizare iterativă de ordinul întâi care este utilizat pentru a găsi minimul local al unei funcții diferențiabile. În termeni simpli, acest algoritm Gradient Descent este folosit pentru a găsi valorile parametrilor (sau coeficienților) unei funcții care sunt utilizați pentru a minimiza o funcție de cost cât mai scăzută posibil. Funcția de cost este utilizată pentru a cuantifica eroarea dintre valorile prezise și valorile reale ale unui model de învățare automată construit.

Intuiție de coborâre în gradient

Luați în considerare un castron mare cu care în mod normal ați păstra fructe sau ați mânca cereale. Acest bol va fi funcția de cost (f).

Acum, o coordonată aleatorie pe orice parte a suprafeței vasului va fi valorile curente ale coeficienților funcției de cost. Fundul vasului este cel mai bun set de coeficienți și este minimul funcției.

Aici, scopul este de a calcula diferitele valori ale coeficienților cu fiecare iterație, de a evalua costul și de a alege coeficienții care au o valoare mai bună a funcției de cost (valoare mai mică). Pe mai multe iterații, s-ar constata că partea inferioară a vasului are cei mai buni coeficienți pentru a minimiza funcția de cost.

În acest fel, algoritmul Gradient Descent funcționează pentru a avea ca rezultat un cost minim.

Alăturați-vă Cursului de învățare automată online de la cele mai bune universități din lume – Master, Programe Executive Postuniversitare și Program de Certificat Avansat în ML și AI pentru a vă accelera cariera.

Procedura de coborâre în gradient

Acest proces de coborâre a gradientului începe cu alocarea inițială a valorilor coeficienților funcției de cost. Aceasta poate fi fie o valoare apropiată de 0, fie o valoare mică aleatorie.

coeficient = 0,0

În continuare, costul coeficienților se obține prin aplicarea acestuia la funcția de cost și calculul costului.

cost = f(coeficient)

Apoi, se calculează derivata funcției de cost. Această derivată a funcției de cost este obținută prin conceptul matematic de calcul diferențial. Ne oferă panta funcției în punctul dat în care se calculează derivata acesteia. Această pantă este necesară pentru a ști în ce direcție va fi mutat coeficientul în următoarea iterație pentru a obține o valoare de cost mai mică. Aceasta se realizează prin observarea semnului derivatei calculate.

delta = derivat(cost)

Odată ce știm ce direcție este în jos față de derivata calculată, trebuie să actualizăm valorile coeficientului. Pentru aceasta, un parametru este cunoscut sub numele de parametru de învățare, se utilizează alfa (α). Acesta este folosit pentru a controla în ce măsură coeficienții se pot schimba cu fiecare actualizare.

coeficient = coeficient – ​​(alfa * delta)

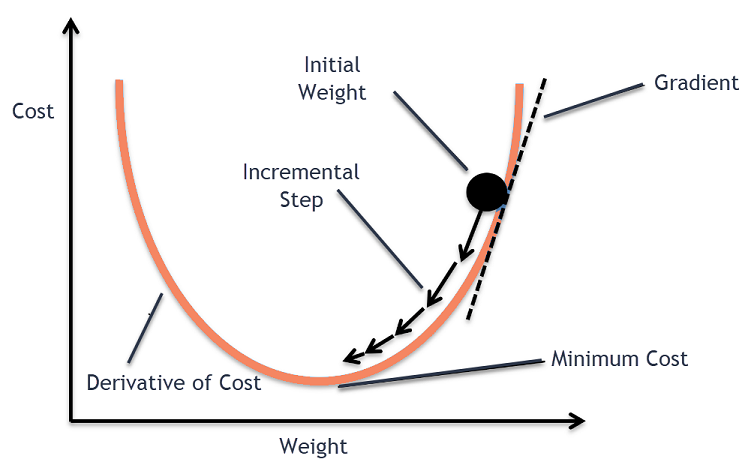
Sursă

În acest fel, acest proces se repetă până când costul coeficienților este egal cu 0,0 sau suficient de aproape de zero. Aceasta este procedura pentru algoritmul de coborâre a gradientului.

Tipuri de algoritmi de coborâre a gradientului

În vremurile moderne, există trei tipuri de bază de Gradient Descent care sunt utilizate în algoritmii moderni de învățare automată și de deep learning. Diferența majoră dintre fiecare dintre aceste 3 tipuri este costul și eficiența sa de calcul. În funcție de cantitatea de date utilizate, de complexitatea timpului și de acuratețe, următoarele sunt cele trei tipuri.

1. Coborâre în grad de lot
2. Coborâre a gradientului stocastic
3. Coborâre cu gradient mini lot

Coborâre gradient lot

Aceasta este prima versiune de bază a algoritmilor Gradient Descent în care întregul set de date este utilizat simultan pentru a calcula funcția de cost și gradientul acesteia. Întrucât întregul set de date este utilizat dintr-o singură dată pentru o singură actualizare, calculul gradientului în acest tip poate fi foarte lent și nu este posibil cu acele seturi de date care sunt în afara capacității de memorie a dispozitivului.

Astfel, acest algoritm Batch Gradient Descent este utilizat numai pentru seturi de date mai mici și când numărul de exemple de antrenament este mare, coborârea batch gradient nu este preferată. În schimb, se folosesc algoritmii Stochastic și Mini Batch Gradient Descent.

Coborâre cu gradient stocastic

Acesta este un alt tip de algoritm de coborâre a gradientului în care este procesat un singur exemplu de antrenament per iterație. În aceasta, primul pas este randomizarea întregului set de date de antrenament. Apoi, un singur exemplu de antrenament este utilizat pentru actualizarea coeficienților. Acest lucru este în contrast cu Coborârea Gradientului Lot în care parametrii (coeficienții) sunt actualizați numai atunci când toate exemplele de antrenament sunt evaluate.

Stochastic Gradient Descent (SGD) are avantajul că acest tip de actualizare frecventă oferă o rată detaliată de îmbunătățire. Cu toate acestea, în anumite cazuri, acest lucru se poate dovedi a fi costisitor din punct de vedere computațional, deoarece procesează un singur exemplu pentru fiecare iterație, ceea ce poate face ca numărul de iterații să fie foarte mare.

Coborâre în gradient mini lot

Acesta este un algoritm dezvoltat recent, care este mai rapid decât algoritmii Batch și Stochastic Gradient Descent. Este de preferat, deoarece este o combinație a ambilor algoritmi menționați anterior. În aceasta, separă setul de antrenament în mai multe mini-loturi și efectuează o actualizare pentru fiecare dintre aceste loturi după calcularea gradientului acelui lot (ca în SGD).

De obicei, dimensiunea lotului variază între 30 și 500, dar nu există o dimensiune fixă, deoarece acestea variază pentru diferite aplicații. Prin urmare, chiar dacă există un set uriaș de date de antrenament, acest algoritm îl procesează în mini-loturi „b”. Astfel, este potrivit pentru seturi mari de date cu un număr mai mic de iterații.

Dacă „m” este numărul de exemple de antrenament, atunci dacă b==m Coborârea Gradient Mini Batch va fi similar cu algoritmul Coborâre Gradient Batch.

Variante de coborâre a gradientului în învățarea automată

Cu această bază pentru Gradient Descent, au existat câțiva alți algoritmi care au fost dezvoltați din aceasta. Câteva dintre ele sunt rezumate mai jos.

Coborâre cu gradient de vanilie

Aceasta este una dintre cele mai simple forme ale tehnicii de coborâre în gradient. Denumirea vanilie înseamnă pură sau fără nicio alterare. În aceasta, se fac pași mici în direcția minimelor prin calcularea gradientului funcției de cost. Similar cu algoritmul menționat mai sus, regula de actualizare este dată de,

coeficient = coeficient – ​​(alfa * delta)

Coborâre în degrade cu Momentum

În acest caz, algoritmul este astfel încât să cunoaștem pașii anteriori înainte de a face pasul următor. Acest lucru se realizează prin introducerea unui nou termen care este produsul actualizării anterioare și a unei constante cunoscute sub numele de impuls. În aceasta, regula de actualizare a greutății este dată de,

actualizare = alfa * delta

viteza = update_anterior * impuls

coeficient = coeficient + viteza – actualizare

ADAGRAD

Termenul ADAGRAD înseamnă algoritmul de gradient adaptiv. După cum spune și numele, folosește o tehnică adaptivă pentru a actualiza greutățile. Acest algoritm este mai potrivit pentru date rare. Această optimizare își modifică ratele de învățare în raport cu frecvența actualizărilor parametrilor în timpul antrenamentului. De exemplu, parametrii care au gradienți mai mari sunt făcuți să aibă o rată de învățare mai lentă, astfel încât să nu ajungem să depășim valoarea minimă. În mod similar, gradienții mai mici au o rată de învățare mai rapidă pentru a se antrena mai repede.

ADAM

Un alt algoritm de optimizare adaptivă care își are rădăcinile în algoritmul Gradient Descent este ADAM, care înseamnă Estimarea momentului adaptiv. Este o combinație a ambelor algoritmi ADAGRAD și SGD cu Momentum. Este construit din algoritmul ADAGRAD și este construit în continuare dezavantaj. În termeni simpli ADAM = ADAGRAD + Momentum.

În acest fel, există câteva alte variante de algoritmi de coborâre a gradientului care au fost dezvoltați și sunt în curs de dezvoltare în lume, cum ar fi AMSGrad, ADAMax.

Concluzie

În acest articol, am văzut algoritmul din spatele unuia dintre cei mai des utilizați algoritmi de optimizare în Machine Learning, algoritmii de coborâre a gradului, împreună cu tipurile și variantele acestuia care au fost dezvoltate.

upGrad oferă un Program Executive PG în Machine Learning și AI și un Master of Science în Machine Learning și AI, care vă poate ghida spre construirea unei cariere. Aceste cursuri vor explica necesitatea învățării automate și pașii suplimentari pentru a culege cunoștințe în acest domeniu, care acoperă concepte variate, de la Coborârea în gradient în învățarea automată.