Bayes naiv gaussian: Ce trebuie să știți?
Publicat: 2021-02-22Cuprins
Bayes naiv gaussian
Naive Bayes este un algoritm probabilistic de învățare automată utilizat pentru multe funcții de clasificare și se bazează pe teorema Bayes. Gaussian Naive Bayes este extensia Bayesului naiv. În timp ce alte funcții sunt folosite pentru a estima distribuția datelor, distribuția Gauss sau normală este cel mai simplu de implementat, deoarece va trebui să calculați media și abaterea standard pentru datele de antrenament.
Ce este algoritmul naiv Bayes?
Naive Bayes este un algoritm probabilistic de învățare automată care poate fi utilizat în mai multe sarcini de clasificare. Aplicațiile tipice ale Naive Bayes sunt clasificarea documentelor, filtrarea spamului, predicția și așa mai departe. Acest algoritm se bazează pe descoperirile lui Thomas Bayes și de aici și numele său.
Numele „Naive” este folosit deoarece algoritmul încorporează caracteristici în modelul său care sunt independente unele de altele. Orice modificare a valorii unei caracteristici nu afectează direct valoarea oricărei alte caracteristici a algoritmului. Principalul avantaj al algoritmului Naive Bayes este că este un algoritm simplu, dar puternic.
Se bazează pe modelul probabilistic în care algoritmul poate fi codificat cu ușurință, iar predicțiile s-au făcut rapid în timp real. Prin urmare, acest algoritm este alegerea tipică pentru a rezolva problemele din lumea reală, deoarece poate fi reglat pentru a răspunde solicitărilor utilizatorilor instantaneu. Dar înainte de a ne scufunda adânc în Bayes naiv și Bayes naiv gaussian, trebuie să știm ce se înțelege prin probabilitate condiționată.
Probabilitatea condiționată explicată
Putem înțelege mai bine probabilitatea condiționată cu un exemplu. Când arunci o monedă, probabilitatea de a trece înainte sau o coadă este de 50%. În mod similar, probabilitatea de a obține un 4 atunci când aruncați zaruri cu fețe este de 1/6 sau 0,16.
Dacă luăm un pachet de cărți, care este probabilitatea de a obține o regină, având în vedere condiția ca aceasta să fie o pică? Deoarece este deja stabilită condiția că trebuie să fie o pică, numitorul sau setul de selecție devine 13. Există o singură damă în pică, deci probabilitatea de a alege o damă de pică devine 1/13= 0,07.

Probabilitatea condiționată a evenimentului A dat eveniment B înseamnă probabilitatea ca evenimentul A să se producă, având în vedere că evenimentul B a avut deja loc. Din punct de vedere matematic, probabilitatea condiționată a lui A dat B poate fi notată ca P[A|B] = P[A AND B] / P[B].
Să luăm în considerare un exemplu puțin complex. Luați o școală cu un total de 100 de elevi. Această populație poate fi delimitată în 4 categorii - studenți, profesori, bărbați și femei. Luați în considerare tabelul de mai jos:
| Femeie | Masculin | Total | |
| Profesor | 8 | 12 | 20 |
| Student | 32 | 48 | 80 |
| Total | 40 | 50 | 100 |
Aici, care este probabilitatea condiționată ca un anumit rezident al școlii să fie Învățător, având în vedere condiția că este Bărbat.
Pentru a calcula acest lucru, va trebui să filtrați sub-populația de 60 de bărbați și să detaliați la cei 12 profesori de sex masculin.
Deci, probabilitatea condiționată așteptată P[Profesor | Masculin] = 12/60 = 0,2
P (Profesor | Masculin) = P (Profesor ∩ Masculin) / P (Bărbat) = 12/60 = 0,2
Acesta poate fi reprezentat ca un Profesor (A) și un bărbat (B) împărțit la bărbat (B). În mod similar, probabilitatea condiționată a lui B dat A poate fi de asemenea calculată. Regula pe care o folosim pentru Naive Bayes poate fi concluzionată din următoarele notații:
P (A | B) = P (A ∩ B) / P(B)
P (B | A) = P (A ∩ B) / P(A)
Regula Bayes
În regula Bayes, mergem de la P (X | Y) care poate fi găsit din setul de date de antrenament pentru a găsi P (Y | X). Pentru a realiza acest lucru, tot ce trebuie să faceți este să înlocuiți A și B cu X și Y în formulele de mai sus. Pentru observații, X ar fi variabila cunoscută și Y ar fi variabila necunoscută. Pentru fiecare rând al setului de date, trebuie să calculați probabilitatea lui Y, având în vedere că X a apărut deja.
Dar ce se întâmplă acolo unde există mai mult de 2 categorii în Y? Trebuie să calculăm probabilitatea fiecărei clase Y pentru a afla cea câștigătoare.
Prin regula Bayes, mergem de la P (X | Y) pentru a găsi P (Y | X)
Cunoscut din datele de antrenament: P (X | Y) = P (X ∩ Y) / P(Y)
P (Dovezi | Rezultat)

Necunoscut – de estimat pentru datele de testare: P (Y | X) = P (X ∩ Y) / P(X)
P (Rezultat | Dovezi)
Regula Bayes = P (Y | X) = P (X | Y) * P (Y) / P (X)
Naivii Bayes
Regula Bayes oferă formula pentru probabilitatea Y dată condiție X. Dar în lumea reală, pot exista mai multe variabile X. Când aveți caracteristici independente, regula Bayes poate fi extinsă la regula Bayes naiv. X-urile sunt independente unele de altele. Formula Naive Bayes este mai puternică decât formula Bayes
Bayes naiv gaussian
Până acum, am văzut că X sunt în categorii, dar cum se calculează probabilitățile când X este o variabilă continuă? Dacă presupunem că X urmează o anumită distribuție, puteți utiliza funcția de densitate de probabilitate a acelei distribuții pentru a calcula probabilitatea probabilităților.
Dacă presupunem că X urmează o distribuție Gaussiană sau normală, trebuie să înlocuim densitatea de probabilitate a distribuției normale și să o numim Gaussian Naive Bayes. Pentru a calcula această formulă, aveți nevoie de media și varianța lui X.
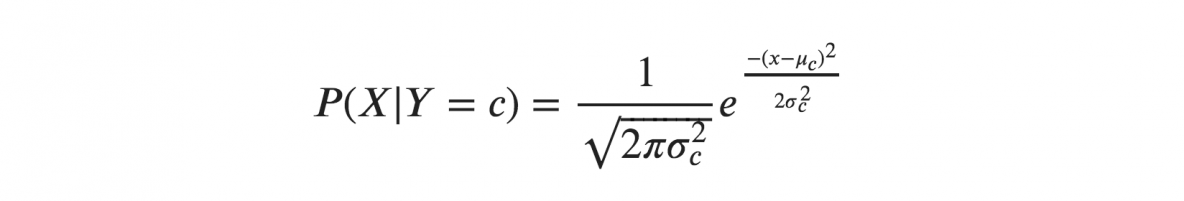
În formulele de mai sus, sigma și mu este varianța și media variabilei continue X calculate pentru o anumită clasă c a lui Y.
Reprezentare pentru Gaussian Naive Bayes
Formula de mai sus a calculat probabilitățile pentru valorile de intrare pentru fiecare clasă printr-o frecvență. Putem calcula media și abaterea standard a lui x pentru fiecare clasă pentru întreaga distribuție.
Aceasta înseamnă că, împreună cu probabilitățile pentru fiecare clasă, trebuie să stocăm și media și abaterea standard pentru fiecare variabilă de intrare pentru clasă.
medie(x) = 1/n * suma(x)
unde n reprezintă numărul de instanțe și x este valoarea variabilei de intrare în date.
abaterea standard(x) = sqrt(1/n * sum(xi-mean(x)^2 ))
Aici se calculează rădăcina pătrată a mediei diferențelor fiecărui x și media lui x unde n este numărul de instanțe, sum() este funcția sumă, sqrt() este funcția rădăcină pătrată și xi este o valoare specifică a x .

Predicții cu modelul Bayes naiv gaussian
Funcția Gaussiană de densitate a probabilității poate fi utilizată pentru a face predicții prin înlocuirea parametrilor cu noua valoare de intrare a variabilei și, ca rezultat, funcția Gaussiană va oferi o estimare pentru probabilitatea noii valori de intrare.
Clasificator Bayes naiv
Clasificatorul Naive Bayes presupune că valoarea unei caracteristici este independentă de valoarea oricărei alte caracteristici. Clasificatorii naivi Bayes au nevoie de date de antrenament pentru a estima parametrii necesari pentru clasificare. Datorită designului și aplicării simple, clasificatoarele Naive Bayes pot fi potrivite în multe scenarii din viața reală.
Concluzie
Clasificatorul Gaussian Naive Bayes este o tehnică de clasificare rapidă și simplă care funcționează foarte bine fără prea mult efort și un nivel bun de precizie.
Dacă sunteți interesat să aflați mai multe despre AI, învățarea automată, consultați Diploma PG de la IIIT-B și upGrad în Învățare automată și AI, care este concepută pentru profesioniști care lucrează și oferă peste 450 de ore de formare riguroasă, peste 30 de studii de caz și sarcini, Statut de absolvenți IIIT-B, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.
Învață cursul ML de la cele mai bune universități din lume. Câștigă programe de master, Executive PGP sau Advanced Certificate pentru a-ți accelera cariera.
Ce este un algoritm bayes naiv?
Naive bayes este un algoritm clasic de învățare automată. Avându-și originea în statistică, bayesul naiv este un algoritm simplu și puternic. Naive bayes este o familie de clasificatoare bazate pe aplicarea unei analize de probabilitate condiționată. În această analiză, probabilitatea condiționată a unui eveniment este calculată folosind probabilitatea fiecăruia dintre evenimentele individuale care constituie evenimentul. Clasificatoarele naive Bayes sunt adesea considerate extrem de eficiente în practică, mai ales când numărul de dimensiuni ale setului de caracteristici este mare.
Care sunt aplicațiile algoritmului naiv bayes?
Naive Bayes este folosit în clasificarea textului, clasificarea documentelor și pentru indexarea documentelor. În Bayes naive, fiecare caracteristică posibilă nu are nicio pondere atribuită în faza de pre-procesare, iar greutățile sunt atribuite ulterior în timpul antrenamentului, precum și în fazele de recunoaștere. Presupunerea de bază a algoritmului bayes naiv este că caracteristicile sunt independente.
Ce este algoritmul Gaussian Naive Bayes?
Gaussian Naive Bayes este un algoritm de clasificare probabilistic bazat pe aplicarea teoremei lui Bayes cu ipoteze puternice de independență. În contextul clasificării, independența se referă la ideea că prezența unei valori a unei trăsături nu influențează prezența alteia (spre deosebire de independența în teoria probabilității). Naiv se referă la utilizarea unei presupuneri că trăsăturile unui obiect sunt independente unele de altele. În contextul învățării automate, clasificatorii naivi Bayes sunt cunoscuți a fi extrem de expresivi, scalabili și rezonabil de precisi, dar performanța lor se deteriorează rapid odată cu creșterea setului de antrenament. O serie de caracteristici contribuie la succesul clasificatorilor naivi Bayes. În special, nu necesită nicio reglare a parametrilor modelului de clasificare, se scalează bine cu dimensiunea setului de date de antrenament și pot gestiona cu ușurință funcțiile continue.
