Diferite tipuri de modele de regresie pe care trebuie să le cunoașteți

Problemele de regresie sunt obișnuite în învățarea automată, iar cea mai comună tehnică de rezolvare a acestora este analiza regresiei. Se bazează pe modelarea datelor și implică elaborarea celei mai bune linii de potrivire, care trece prin toate punctele de date, astfel încât distanța dintre linie și fiecare punct de date să fie minimă. Deși există multe tehnici diferite de analiză a regresiei, regresia liniară și cea logistică sunt cele mai proeminente. Tipul de model de analiză de regresie pe care îl folosim va depinde în cele din urmă de natura datelor implicate.

Să aflăm mai multe despre analiza de regresie și despre diferitele tipuri de modele de analiză de regresie.

Ce este analiza de regresie?

Analiza regresiei este o tehnică de modelare predictivă pentru determinarea relației dintre variabilele dependente (țintă) și variabilele independente dintr-un set de date. Este utilizată de obicei atunci când variabila țintă conține valori continue, iar variabilele dependente și independente au o relație liniară sau neliniară. Astfel, tehnicile de analiză de regresie își găsesc utilizare în determinarea relației de efect cauzal dintre variabile, modelarea seriilor de timp și prognoză. De exemplu, relația dintre vânzările și cheltuielile publicitare ale unei companii poate fi studiată cel mai bine folosind analiza de regresie.

Tipuri de analiză de regresie

Există multe tipuri diferite de tehnici de analiză de regresie pe care le putem folosi pentru a face predicții. În plus, utilizarea fiecărei tehnici este determinată de factori precum numărul de variabile independente, forma liniei de regresie și tipul de variabilă dependentă.

Să înțelegem câteva dintre cele mai frecvent utilizate metode de analiză de regresie:

1. Regresia liniară

Regresia liniară este cea mai cunoscută tehnică de modelare și presupune o relație liniară între o variabilă dependentă (Y) și o variabilă independentă (X). Ea stabilește această relație liniară folosind o linie de regresie, cunoscută și ca linie de cea mai bună potrivire. Relația liniară este reprezentată de ecuația Y = c+m*X + e, unde „c” este intersecția, „m” este panta dreptei și „e” este termenul de eroare.

Modelul de regresie liniară poate fi simplu (cu o variabilă dependentă și o variabilă independentă) sau multiplu (cu o variabilă dependentă și mai multe variabile independente).

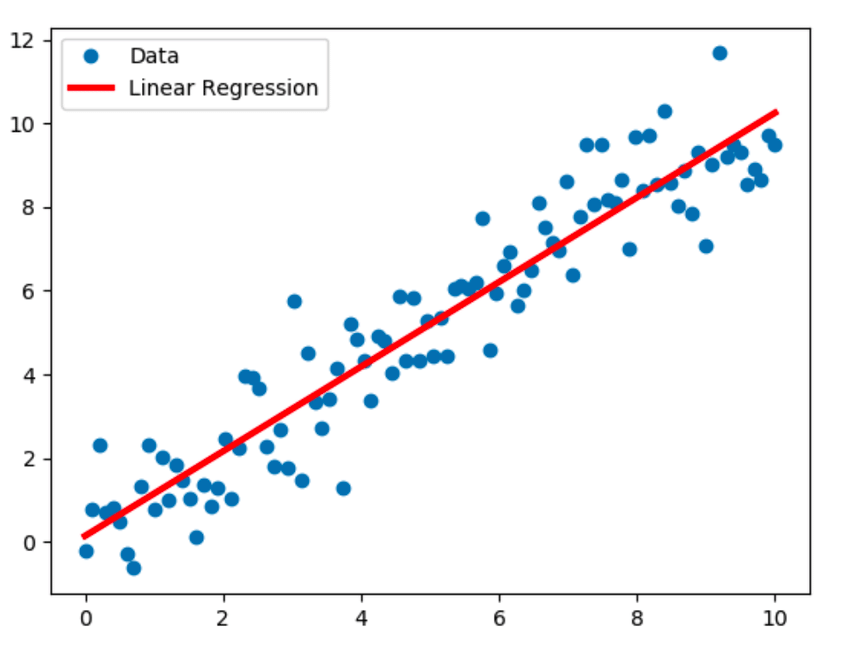
Sursă

2. Regresia logistică

Tehnica analizei regresiei logistice își găsește utilizare atunci când variabila dependentă este discretă. Cu alte cuvinte, această tehnică este utilizată pentru a estima probabilitatea unor evenimente care se exclud reciproc, cum ar fi trecere/eșec, adevărat/fals, 0/1 etc. Prin urmare, variabila țintă poate avea doar una dintre două valori, iar o curbă sigmoidă reprezintă relația sa cu variabila independentă. Valoarea probabilității variază între 0 și 1.

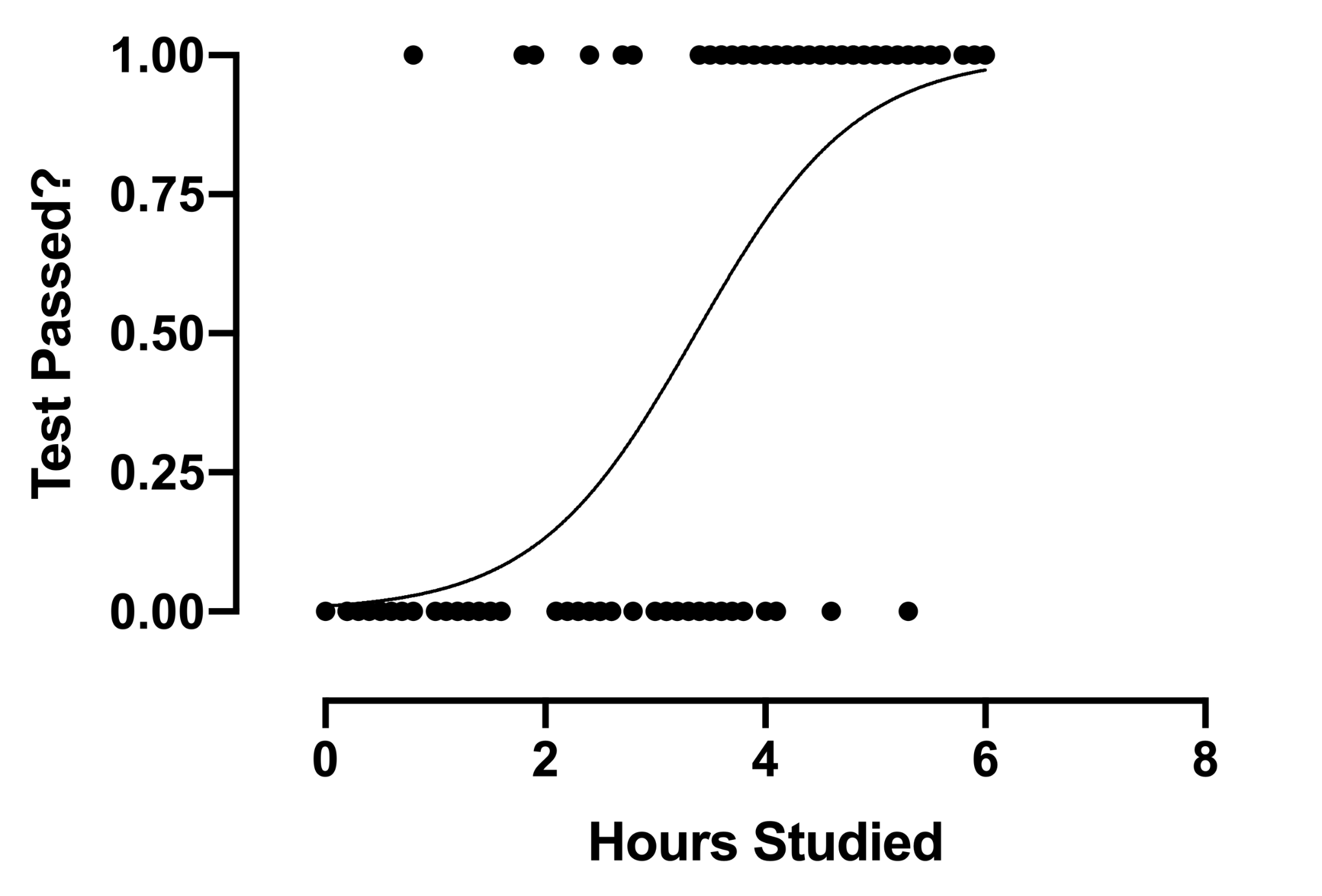
Sursă

3. Regresia polinomială

Tehnica analizei regresiei polinomiale modelează o relație neliniară între variabilele dependente și independente. Este o formă modificată a modelului de regresie liniară multiplă, dar linia de cea mai bună potrivire care trece prin toate punctele de date este curbă și nu dreaptă.

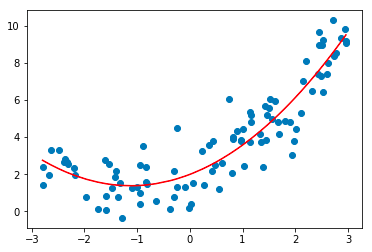
Sursă

4. Regresia crestei

Tehnica de analiză a regresiei crestei este utilizată atunci când datele arată multicoliniaritate; adică variabilele independente sunt foarte corelate. Deși estimările celor mai mici pătrate în multicoliniaritate sunt imparțial, varianțele lor sunt suficient de mari pentru a abate valoarea observată de la valoarea adevărată. Regresia Ridge minimizează erorile standard prin introducerea unui grad de părtinire în estimările de regresie.

Lambda (λ) din ecuația de regresie a crestei rezolvă problema multicoliniarității.

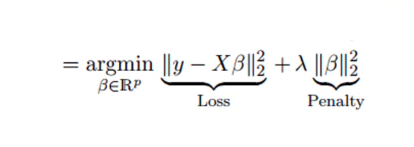
Sursă

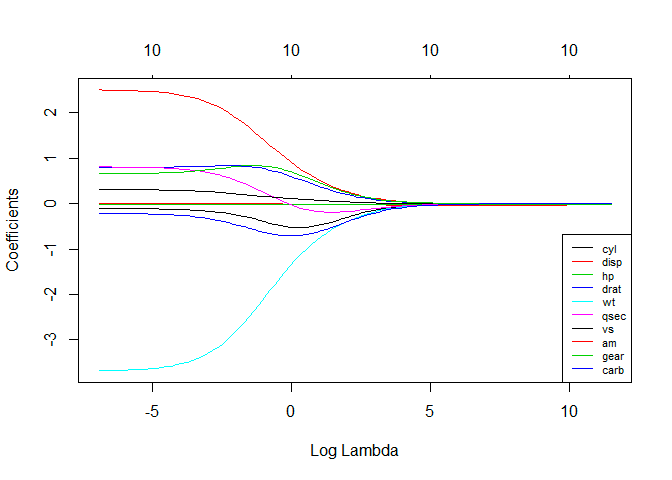
Sursă

5. Regresia lazo

La fel ca regresia crestei, tehnica de regresie lasso (operator de contracție și selecție minimă absolută) penalizează dimensiunea absolută a coeficientului de regresie. În plus, tehnica de regresie lasso folosește selecția variabilelor, ceea ce are ca rezultat micșorarea valorilor coeficienților către zero absolut.

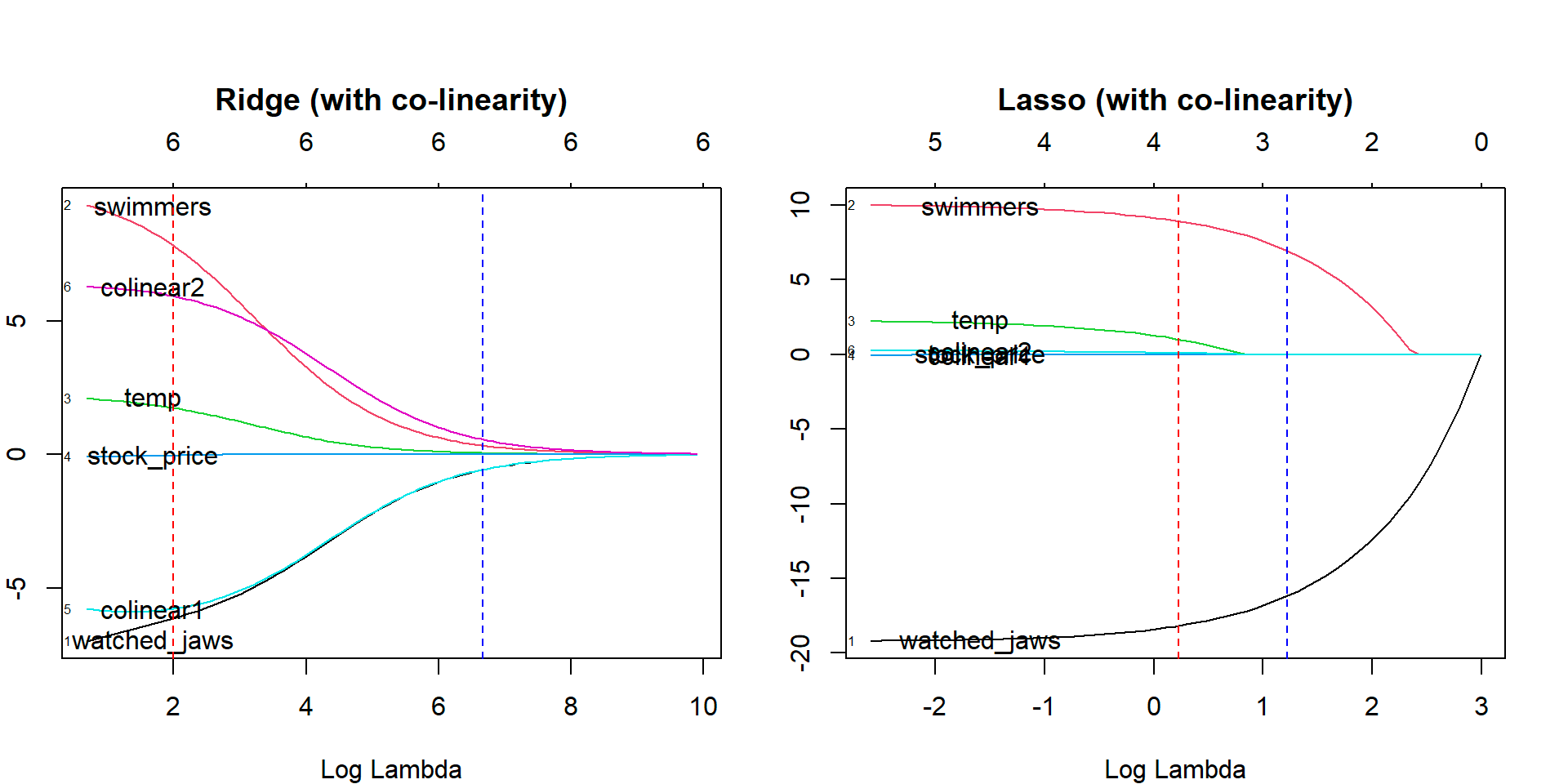
Sursă

6. Regresia cuantilă

Tehnica analizei regresiei cuantile este o extensie a analizei regresiei liniare. Este utilizat atunci când condițiile pentru regresia liniară nu sunt îndeplinite sau datele au valori aberante. Regresia cuantilă își găsește aplicații în statistică și econometrie.

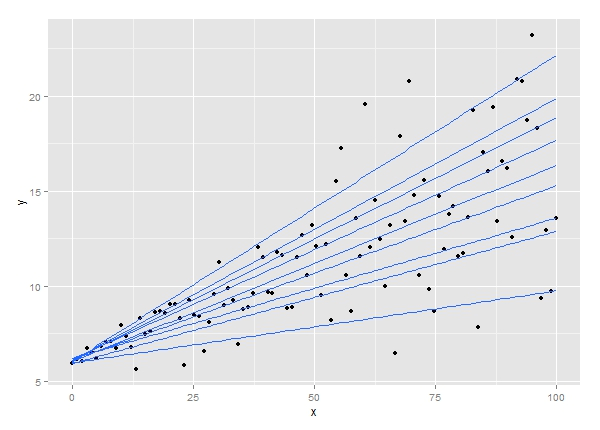
Sursă

7. Regresia liniară bayesiană

Regresia liniară bayesiană este unul dintre tipurile de tehnici de analiză a regresiei în învățarea automată care utilizează teorema lui Bayes pentru a determina valoarea coeficienților de regresie. În loc să afle cele mai mici pătrate, această tehnică determină distribuția posterioară a caracteristicilor. Ca rezultat, tehnica are mai multă stabilitate decât regresia liniară simplă.

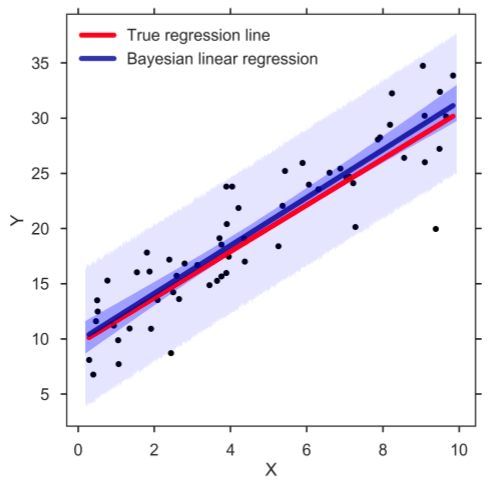
Sursă

8. Regresia componentelor principale

Tehnica de regresie a componentelor principale este utilizată de obicei pentru a analiza datele de regresie multiplă cu multicoliniaritate. La fel ca tehnica de regresie a crestei, metoda de regresie a componentelor principale minimiza erorile standard prin conferirea unui grad de partajare estimărilor de regresie. Tehnica are două etape – în primul rând, analiza componentelor principale este aplicată datelor de antrenament, iar apoi, eșantioanele transformate sunt folosite pentru a antrena un regresor.

9. Regresie parțială cu cele mai mici pătrate

Tehnica de regresie parțială cu cele mai mici pătrate este unul dintre tipurile rapide și eficiente de tehnici de analiză a regresiei bazate pe covarianță. Este benefic pentru problemele de regresie în care numărul de variabile independente este mare, cu probabilitate multicoliniaritate între variabile. Tehnica reduce variabilele la un set mai mic de predictori, care sunt apoi utilizați pentru a efectua o regresie.

10. Regresia netă elastică

Tehnica de regresie a rețelei elastice este un hibrid al modelelor de regresie laso și creste și este utilă atunci când se ocupă de variabile foarte corelate. Folosește penalizările din metodele de regresie cu creasta și lazo pentru a regulariza modelele de regresie.

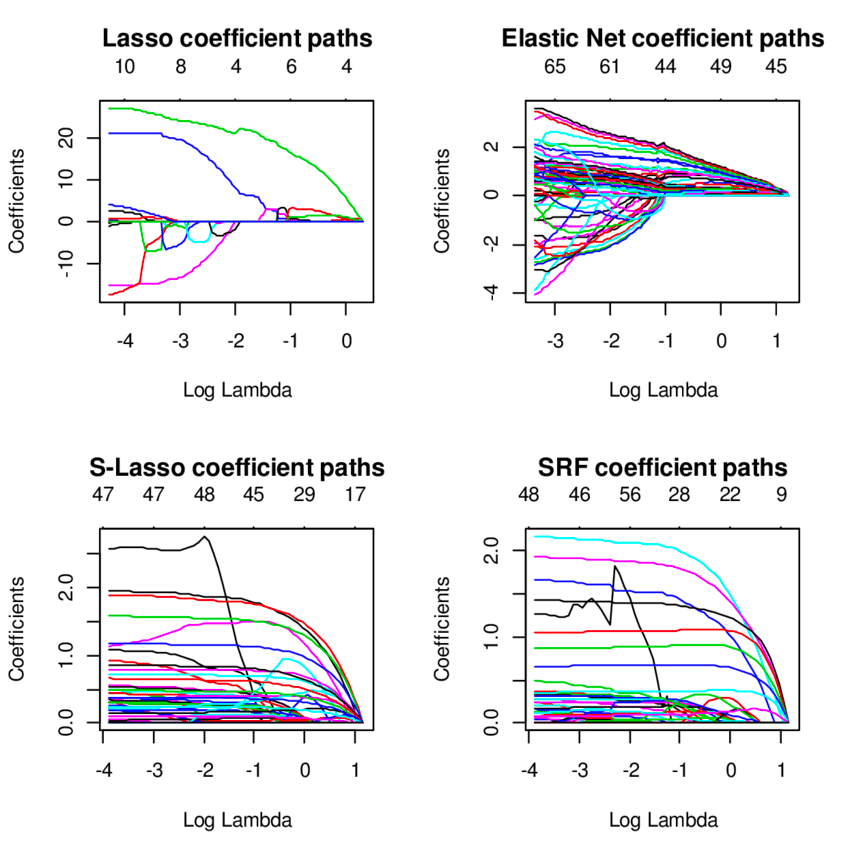
Sursă

rezumat

În afară de tehnicile de analiză a regresiei pe care le-am discutat aici, în învățarea automată sunt utilizate câteva alte tipuri de modele de regresie, cum ar fi regresia ecologică, regresia în trepte, regresia jackknife și regresia robustă. Cazul de utilizare specific al tuturor acestor tipuri diferite de tehnici de regresie depinde de natura datelor disponibile și de nivelul de acuratețe care poate fi atins. În general, analiza de regresie are două beneficii principale. Acestea sunt după cum urmează:

• Indică relația dintre o variabilă dependentă și o variabilă independentă.

• Ea arată puterea impactului variabilelor independente asupra unei variabile dependente.

Calea înainte: obțineți o diplomă de master în învățare automată și inteligență artificială

Ești în căutarea unui program online cuprinzător pentru a te pregăti pentru o carieră de învățare automată și inteligență artificială?

upGrad oferă o diplomă de master în învățare automată și inteligență artificială în asociere cu Universitatea Liverpool John Moores și IIIT Bangalore pentru a produce profesioniști AI versatili și oameni de știință ai datelor.

Programul online cuprinzător, de 20 de luni, este conceput special pentru profesioniștii care doresc să stăpânească concepte și abilități avansate precum Deep Learning, NLP, Modele grafice, Reinforcement Learning și altele asemenea. În plus, programul intenționează să ofere o bază solidă în statistică, împreună cu limbaje și instrumente cheie de programare, cum ar fi Python, Keras, TensorFlow, Kubernetes, MySQL și multe altele.

Repere ale programului:

• Masterat de la Universitatea John Moores din Liverpool
• PGP executiv de la IIIT Bangalore
• Peste 40 de sesiuni live, peste 12 studii de caz și proiecte, 11 sarcini de codare, șase proiecte de bază
• Peste 25 de sesiuni de mentorat cu experți din industrie
• Asistență în carieră la 360 de grade și sprijin pentru învățare
• Oportunități de creare de rețele peer-to-peer

Cu o facultate de clasă mondială, experți în pedagogie, tehnologie și industrie, upGrad a devenit cea mai mare platformă EdTech superioară din Asia de Sud și a afectat peste 500.000 de profesioniști din întreaga lume. Înscrie-te astăzi pentru a deveni parte a celor peste 40.000 de cursanți la nivel mondial upGrad din peste 80 de țări!