Actualizarea animației CSS cu curbe de mișcare

Există animație UI și apoi animație UI bună . O animație bună te face să faci „Wow!” — este neted, frumos și, mai ales, natural, nu blocat, rigid sau robotizat. Dacă frecventezi Dribbble sau UpLabs, vei ști despre ce vorbesc.

Citiri suplimentare despre Smashing:

• Animații SVG și CSS cu traseu clip
• Tehnici practice de animație
• Crearea de animații „desenate manual” cu SVG
• Noul API de animație web

Cu atât de mulți designeri uimitori care creează astfel de animații frumoase, orice dezvoltator ar dori în mod natural să le recreeze în propriile proiecte. Acum, CSS oferă unele presetări pentru transition-timing-function , cum ar fi ease-in , ease-out și ease-in-out , care adaugă un anumit nivel de netezime și realism, dar sunt foarte generice, nu-i așa? Cât de plictisitor ar fi dacă fiecare animație de pe web ar urma aceleași trei funcții de sincronizare?

Una dintre proprietățile transition-timing-function este cubic-bezier(n1, n2, n3, n4) , în care puteți trece patru numere pentru a vă crea propria funcție de sincronizare. Spre sfârșitul acestui articol, veți ști exact ce reprezintă aceste patru numere - totuși, credeți-mă, să veniți cu patru numere pentru a surprinde tranziția pe care o imaginați în capul vostru nu este deloc ușor de făcut. Dar datorită lui cubic-bezier și Ceasar, nu trebuie. Aceste instrumente aduc curbe de mișcare pe web.

Curbele de mișcare sunt utilizate în principal de animatori (de exemplu, în Adobe After Effects) pentru a crea animații avansate, realiste. Cu cubic-bezier și Ceasar, puteți manipula pur și simplu forma unei curbe, iar acele patru numere ( n1, n2, n3, n4 ) vor fi completate pentru dvs., ceea ce este absolut grozav! Totuși, pentru a utiliza și a profita la maximum de curbele de mișcare, trebuie să înțelegeți cum funcționează acestea și asta vom face în acest articol. Sa incepem.

Înțelegerea curbelor de mișcare

O curbă de mișcare nu este altceva decât o diagramă între orice proprietate animabilă și timp. O curbă de mișcare definește modul în care viteza unei animații care rulează sub influența sa variază în timp.

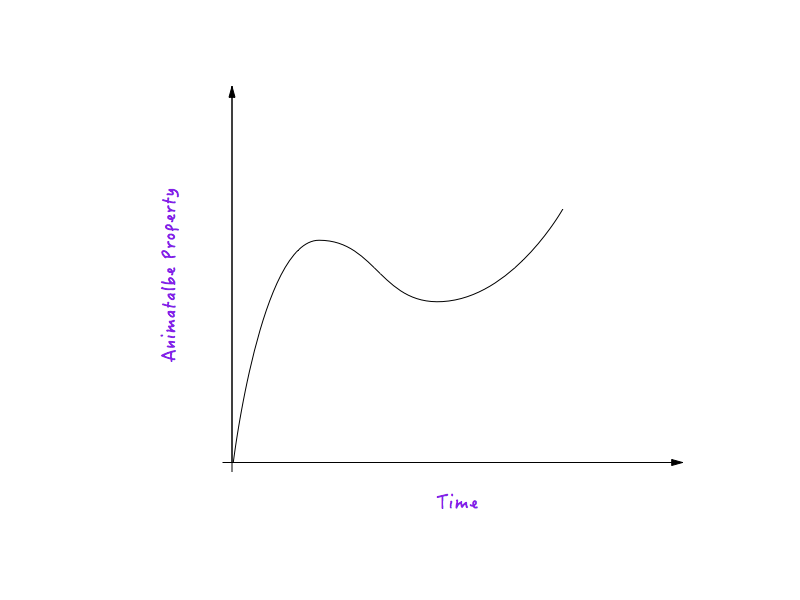
Să luăm distanța ( translateX ) ca exemplu de proprietate animabilă. (Explicația este valabilă pentru orice altă proprietate animabilă.)

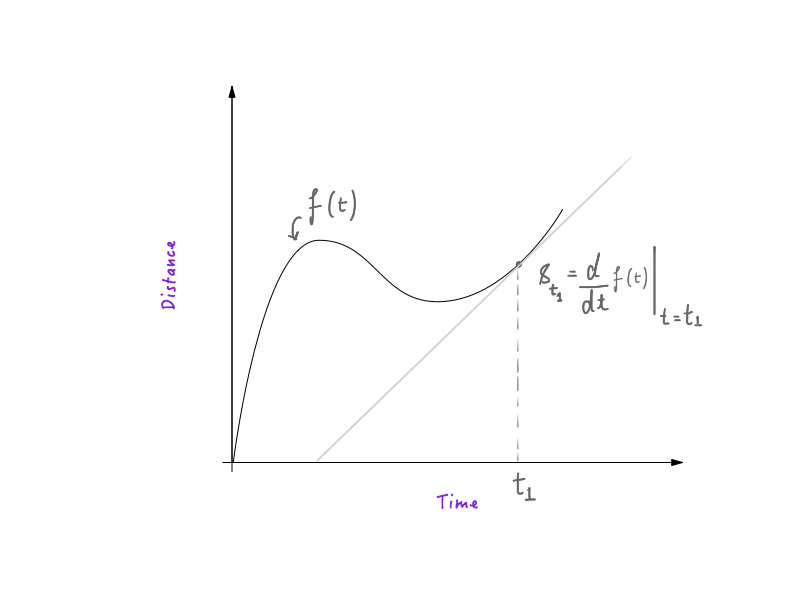
Dacă ați avut experiență cu fizica și calculul de bază, veți ști că descifrarea vitezei dintr-un grafic distanță-timp este foarte simplă. Prima derivată a distanței în funcție de timp , în raport cu timpul , este viteza, ceea ce înseamnă că un obiect care urmează o curbă distanță-timp ar avea o viteză mai mare în locurile în care curba este abruptă și mai mică în locurile în care curba este mai plată. . Dacă știi cum funcționează, grozav! Sunteți gata și puteți sări la secțiunea următoare.

Acum, sunt conștient de faptul că proiectarea și dezvoltarea este un domeniu divers și nu toată lumea are același background. Poate că cele două paragrafe de mai sus au fost toate jargon pentru tine. Nu te supăra. Vom continua și vom înțelege jargonul.

Luați în considerare caseta roșie de mai jos. Să luăm puțină callow aici și să numim caseta roșie „Boxy”; va fi mai ușor să te referi la asta în acest fel. Bine, deci Boxy se va muta de la o margine la alta a ecranului într-un mod liniar și vom analiza mișcarea acestuia.

Una dintre presetări ale transition-timing-function este linear . Pentru a-l face pe Boxy să se miște, tot ce facem este să adăugăm următoarea clasă.

 .moveForward { transform: translateX(1000px); }

Pentru a controla animația, am seta proprietatea de transition pentru Boxy după cum urmează:

 #boxy { width: 200px; height: 200px; background: red; transition-property: transform; transition-duration: 1s; transition-timing-function: linear; }

Acesta este un mod foarte pronunțat de a specifica transition . În realitate, aproape întotdeauna veți găsi transition scrisă în forma ei scurtă:

 #boxy { width: 200px; height: 200px; background: red; transition: transform 1s linear; }

Să vedem că merge.

Robotic, nu-i așa? Ați putea spune că această mișcare pare robotică deoarece este liniară, ceea ce este un răspuns perfect plauzibil. Dar ai putea explica de ce? Putem vedea că stabilirea linear are ca rezultat mișcarea robotică, dar ce se întâmplă exact în spatele scenei? Asta ne vom da seama mai întâi; vom ajunge la interior și vom înțelege de ce această mișcare pare robotică, blocată și nu naturală.

Să începem prin a reprezenta grafic mișcarea lui Boxy pentru a vedea dacă putem obține o perspectivă. Graficul nostru va avea două axe, prima fiind distanța și a doua timp. Boxy acoperă o distanță totală de 1000 de pixeli (distanță) în 1 secundă (timp). Acum, nu vă speriați de toate matematicile de mai jos - este foarte simplu.

Iată graficul nostru foarte simplu, cu axele așa cum am menționat.

Chiar acum, este gol. Să-l completăm cu câteva date.

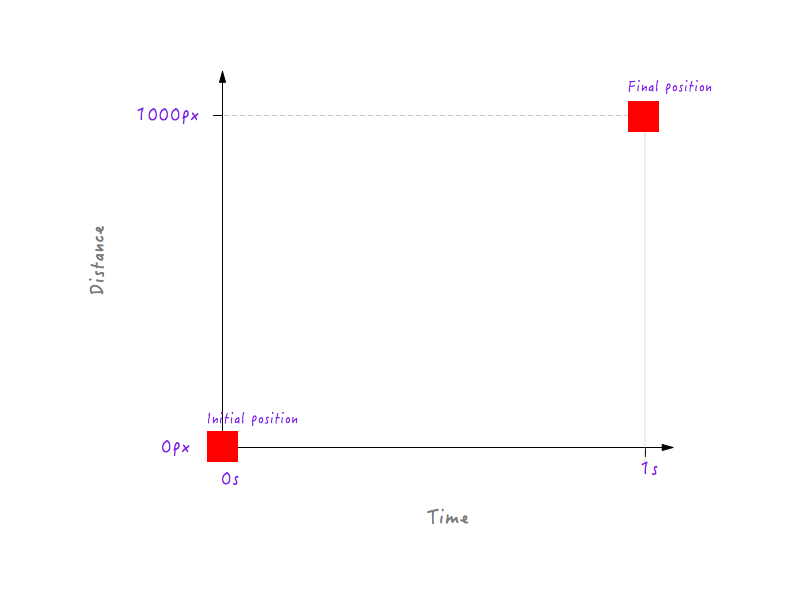
Pentru început, știm că la 0 secunde, când animația nu a început încă, Boxy se află în poziția inițială (0 pixeli). Și după ce a trecut 1 secundă, Boxy a parcurs un total de 1000 de pixeli, ajungând pe marginea opusă a afișajului.

Să reprezentăm aceste date pe grafic.

Până acum, bine. Dar două puncte de date nu sunt suficiente - avem nevoie de mai multe. Următoarea figură arată pozițiile lui Boxy în diferite momente de timp (toate datorită camerei mele de mare viteză).

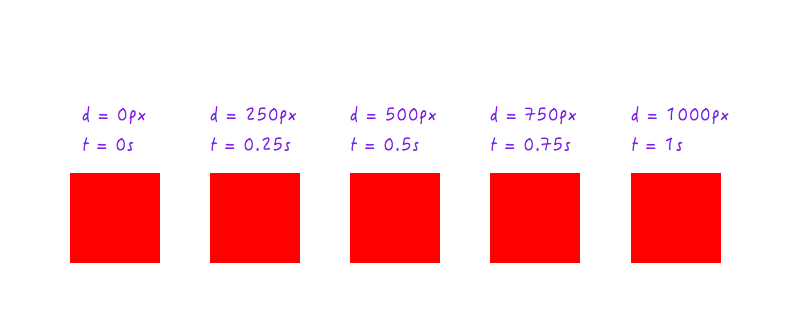
Să adăugăm aceste date la graficul nostru.

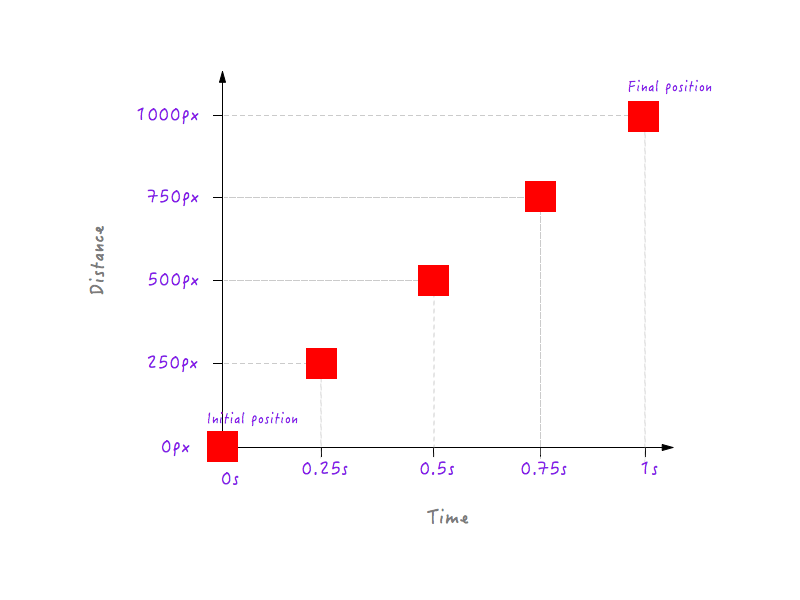
Desigur, puteți avea mai multe puncte de date pentru timpi diferiți (de exemplu, 0,375 secunde, 0,6 secunde etc.), dar ceea ce avem este suficient pentru a ne completa graficul. Unind toate punctele, am completat graficul. Bate palma!

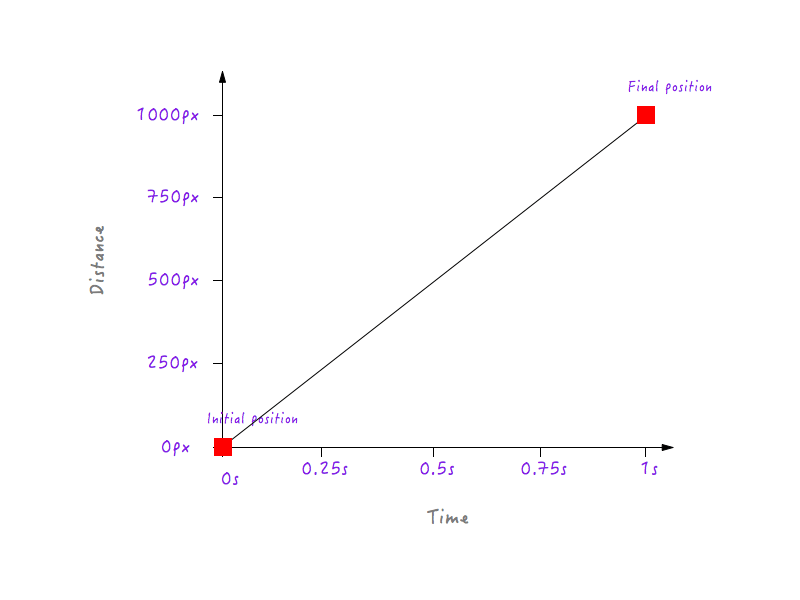
Cool, dar ce ne spune asta? Îți amintești că ne-am început investigația cu scopul de a înțelege de ce mișcarea liniară a lui Boxy este nenaturală și robotică? La o privire, acest grafic pe care tocmai l-am construit nu ne spune nimic despre asta. Trebuie să mergem mai adânc.

Tine cont de grafic si hai sa vorbim un minut despre viteza. Știu că știi ce este viteza — aș dori doar să o exprim în termeni matematici. În continuare, formula vitezei este următoarea:

Prin urmare, dacă o mașină parcurge o distanță de 100 de kilometri într-o oră, spunem că viteza ei este de 100 de kilometri pe oră.

Dacă mașina își dublează viteza, va începe să parcurgă dublul distanței (200 de kilometri) în același interval (1 oră), sau, cu alte cuvinte, va parcurge distanța inițială de 100 de kilometri în jumătate de timp (0,5 ore). . Are sens?

În mod similar, dacă mașina și-ar înjumătăți viteza (adică încetinește la jumătate), ar începe să parcurgă o distanță de 50 de kilometri în același interval (1 oră), sau, cu alte cuvinte, ar parcurge distanța inițială de 100 de kilometri. kilometri în timp de două ori (2 ore).

Grozav! Cu asta din drum, să reluăm de unde am rămas. Încercam să ne dăm seama cum graficul dintre distanță și timp ne poate ajuta să înțelegem de ce mișcarea liniară a lui Boxy se simte robotică.

Hei, așteaptă o secundă! Avem un grafic între distanță și timp, iar viteza poate fi calculată din distanță și timp, nu-i așa? Să încercăm să calculăm viteza lui Boxy la diferite intervale de timp.

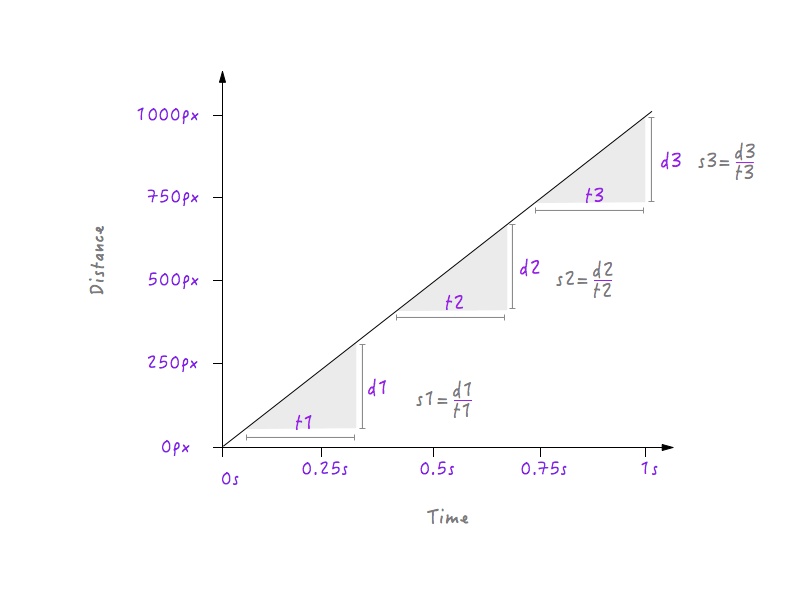
Aici, am ales trei intervale de timp diferite: unul lângă început, unul la mijloc și unul la sfârșit, lângă poziția finală. După cum este evident, la toate cele trei intervale, Boxy are exact aceeași viteză (s1 = s2 = s3) de 1000 de pixeli pe secundă; adică indiferent de intervalul pe care îl alegeți în graficul de mai sus, îl veți găsi pe Boxy mișcându-se la 1000 de pixeli pe secundă. Nu este ciudat? Lucrurile din viața reală nu se mișcă cu o viteză constantă; pornesc încet, își măresc treptat viteza, se mișcă un timp și apoi încetinesc din nou înainte de a se opri, dar Boxy începe brusc cu o viteză de 1000 de pixeli pe secundă, mișcându-se cu aceeași viteză și oprindu-se brusc la exact aceeași viteză. Acesta este motivul pentru care mișcarea lui Boxy pare robotică și nefirească. Va trebui să ne schimbăm graficul pentru a remedia acest lucru. Dar înainte de a ne scufunda, va trebui să știm cum vor afecta modificările vitezei graficul desenat între distanță și timp. Gata? Asta o să fie amuzant.

Să dublăm viteza lui Boxy și să vedem cum se schimbă aspectul graficului ca răspuns. Viteza originală a lui Boxy, așa cum am calculat mai sus, este de 1000 de pixeli pe secundă. Pentru că am dublat viteza, Boxy va putea acum să parcurgă distanța de 1000 de pixeli în jumătate din timp, adică în 0,5 secunde. Să punem asta pe un grafic.

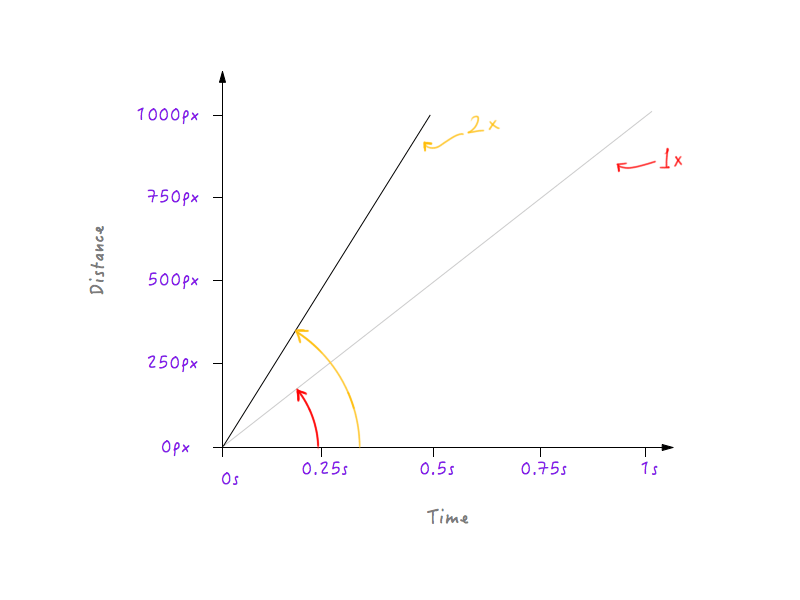
Dacă triplăm viteza? Boxy acoperă acum 1000 de pixeli într-o treime din timp (o treime de secundă).

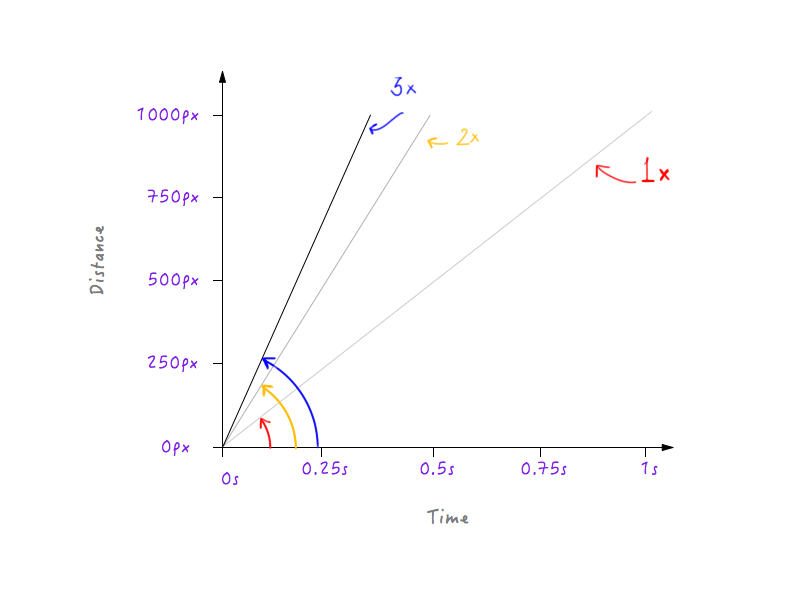
Hmm, ai observat ceva? Observați cum, atunci când graficul se schimbă, unghiul pe care linia îl face cu axa timpului crește pe măsură ce viteza crește.

În regulă, să mergem înainte și să reducem la jumătate viteza lui Boxy. Reducerea la jumătate a vitezei înseamnă că Boxy va putea acoperi doar 500 de pixeli (jumătate din distanța inițială) într-o secundă. Să punem asta pe un grafic.

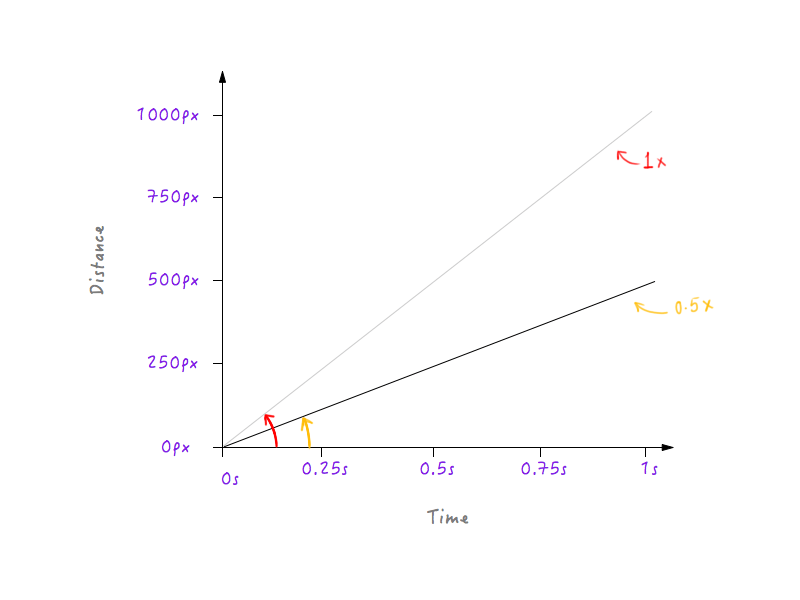
Să încetinim mai mult Boxy, făcând viteza la o treime față de cea originală. Boxy va putea acoperi o treime din distanța inițială în 1 secundă.

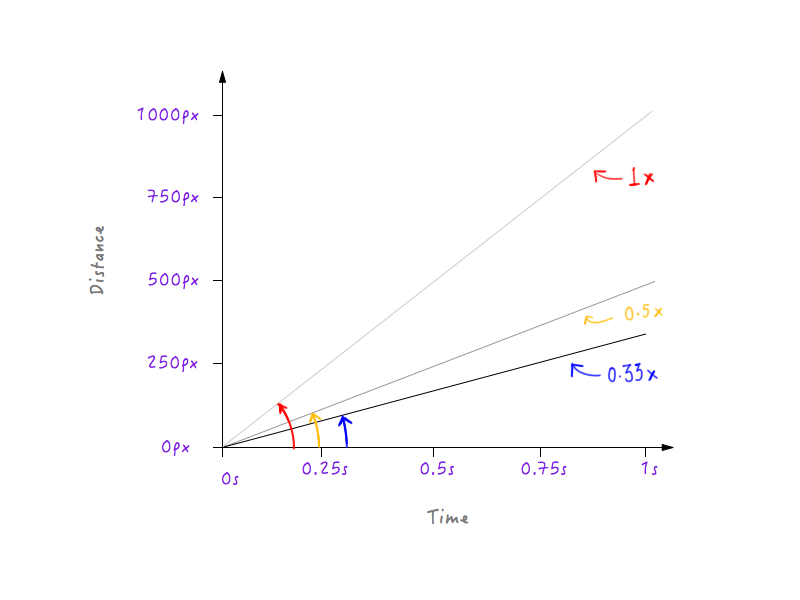
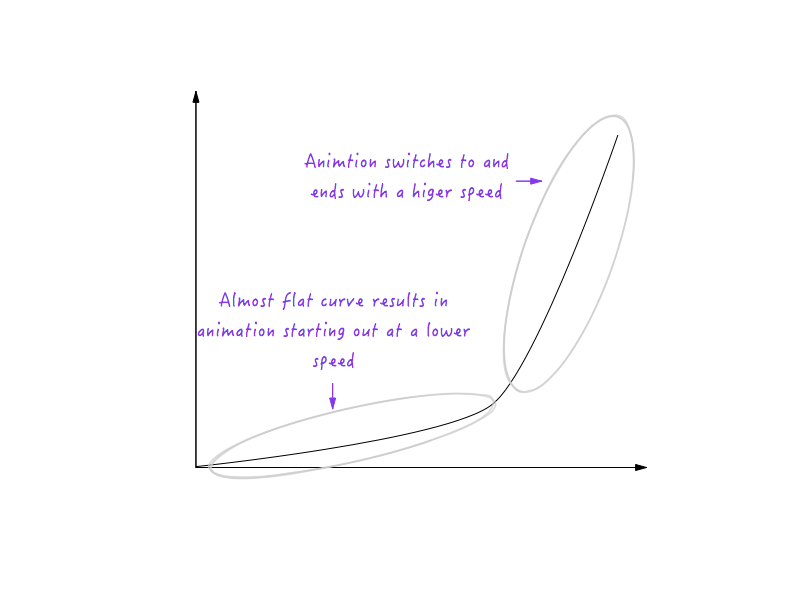
Vezi un model? Linia devine din ce în ce mai abruptă pe măsură ce creștem viteza lui Boxy și începe să se aplatizeze pe măsură ce îl încetinim pe Boxy.

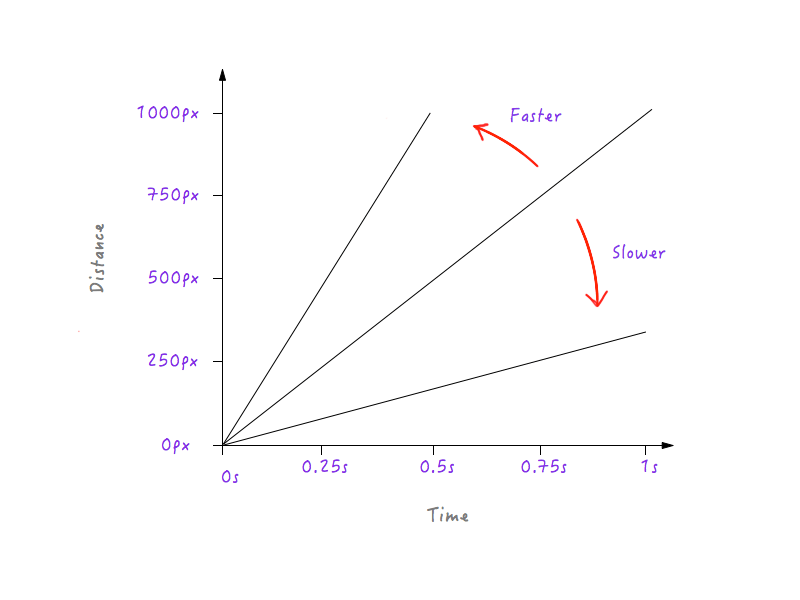
Acest lucru are sens deoarece, pentru o linie mai abruptă, un mic progres în timp produce o schimbare mult mai mare a distanței, implicând o viteză mai mare.

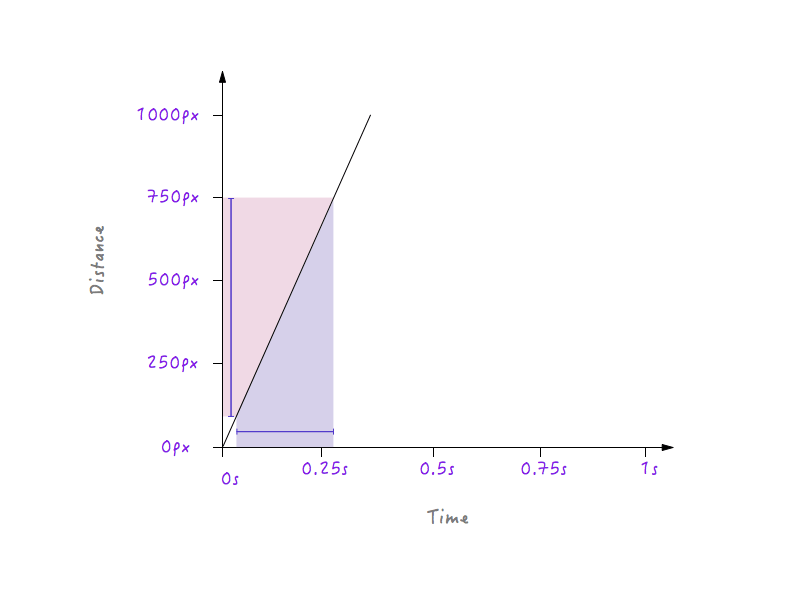
Pe de altă parte, pentru o linie mai puțin abruptă, o schimbare mare a timpului produce doar o mică modificare a distanței, adică o viteză mai mică.

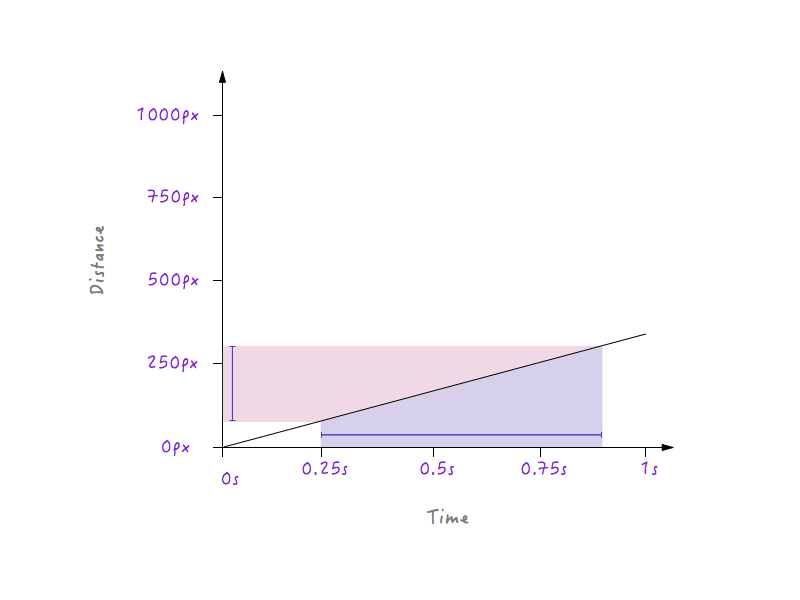
Cu toate schimbările pe care le-am făcut, Boxy se mișcă în continuare într-o manieră liniară, doar la viteze diferite. Cu toate acestea, având în vedere noile noastre cunoștințe despre modul în care modificările distanței în raport cu timpul pot afecta viteza, putem experimenta și desena un grafic care să-l facă pe Boxy să se miște într-un mod care să pară natural și realist.

Să o luăm pas cu pas. În primul rând, lucrurile în viața reală încep încet și cresc încet în viteză. Deci, hai să facem asta.

În toate iterațiile graficului prezentat mai jos, veți observa că punctele din colțurile opuse rămân fixe. Acest lucru se datorează faptului că nu modificăm durata pentru care rulează animația și nici distanța pe care Boxy o parcurge.

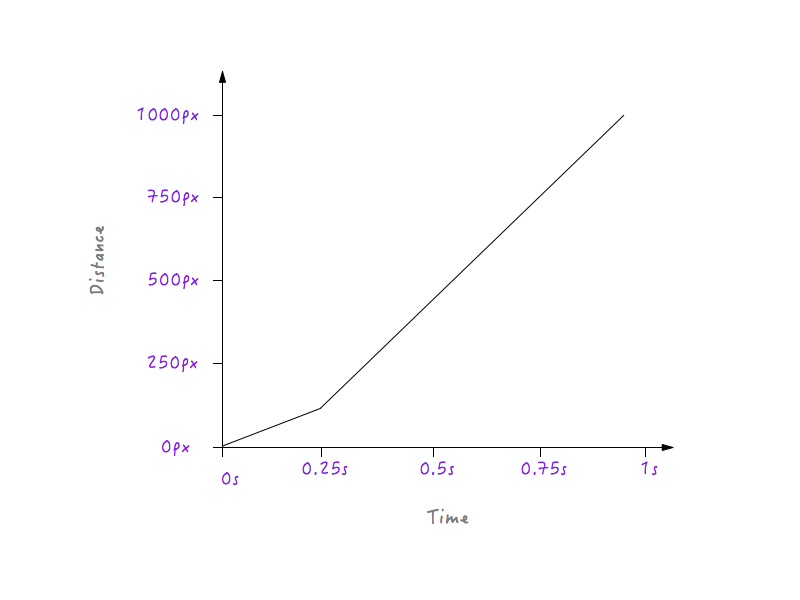
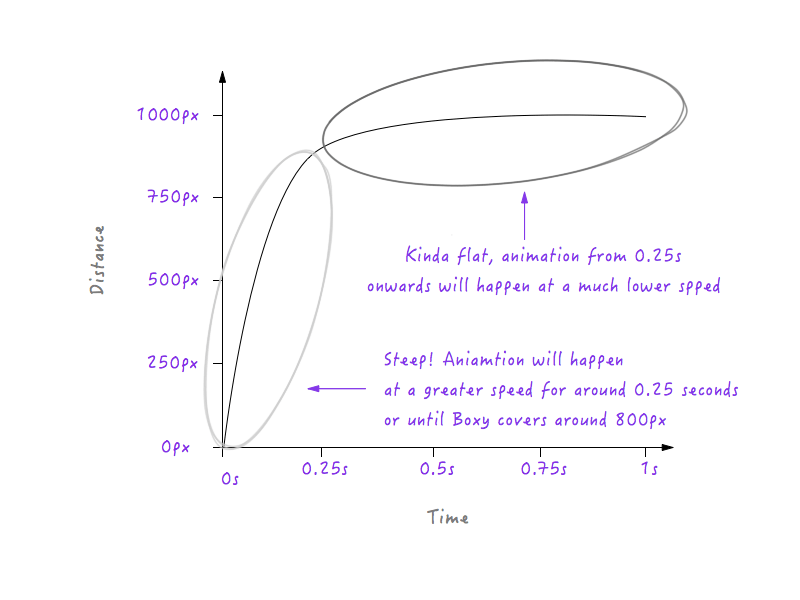
Dacă Boxy urmează să urmeze graficul de mai sus, se va deplasa cu o viteză mai mică timp de 0,25 secunde, deoarece linia este mai puțin abruptă începând de la 0 la 0,25 secunde, iar apoi va trece brusc la o viteză mai mare după 0,25 secunde (motivul fiind că linia din grafic devine mai abruptă după 0,25 secunde). Totuși, va trebui să netezim această tranziție; nu vrem colțuri — până la urmă se numește curbă de mișcare. Să transformăm acel colț într-o curbă.

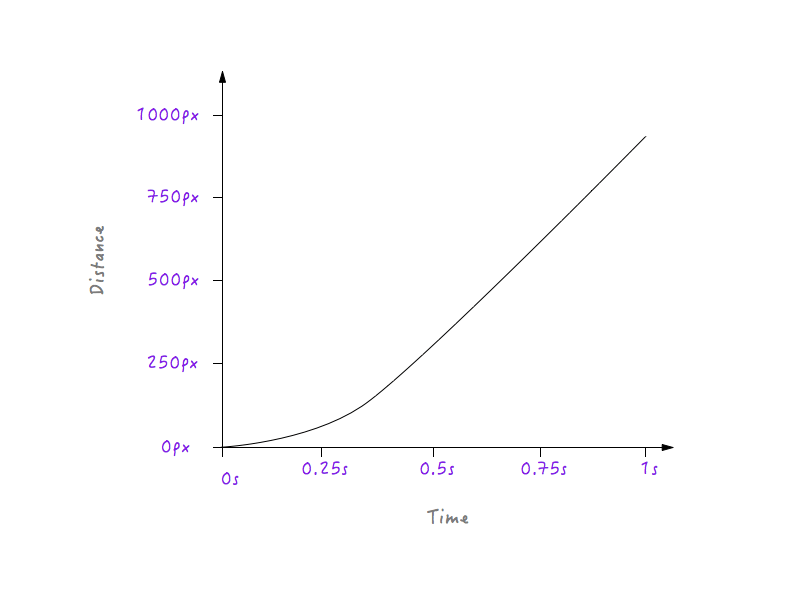
Observați tranziția lină pe care o trece Boxy de la starea de repaus la creșterea treptată a vitezei.

Bun! Apoi, obiectele din viața reală încetinesc progresiv înainte de a se opri. Să schimbăm graficul pentru a face acest lucru. Din nou, vom relua un moment după care ne-am dori ca Boxy să înceapă să încetinească. Ce zici de aproximativ 0,6 secunde? Am netezit deja colțul tranziției la o curbă aici.

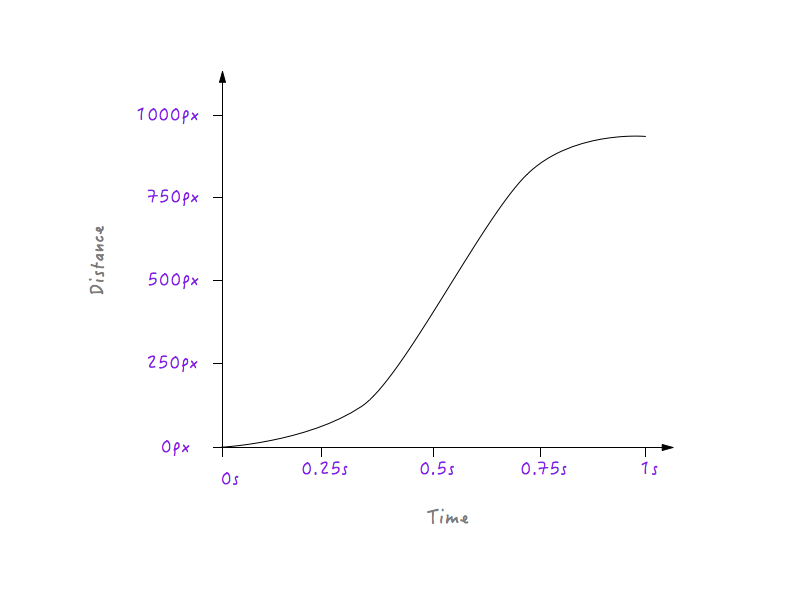
Uită-te la Boxy go! Mult mai natural, nu-i așa?

Curba pe care am trasat-o în locul colțului este de fapt o colecție de multe segmente de linie mici; și, după cum știți deja, cu cât linia de pe grafic este mai abruptă, cu atât viteza este mai mare și cu cât linia este mai plată, cu atât viteza este mai mică. Observați cum, în partea stângă a imaginii, segmentele de linie care alcătuiesc curba devin din ce în ce mai abrupte, ceea ce duce la o creștere treptată a vitezei și se aplatizează progresiv pe partea dreaptă, ceea ce duce la o scădere progresivă a vitezei?

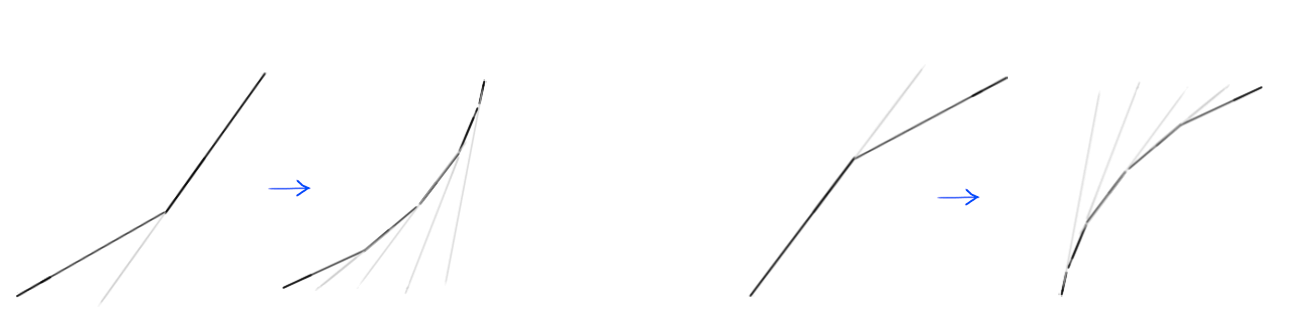
Cu toate aceste cunoștințe, înțelegerea curbelor de mișcare devine mult mai ușoară. Să ne uităm la câteva exemple.

Utilizarea curbelor de mișcare în animația UI

Data viitoare când va trebui să animați un element UI, veți avea la dispoziție puterea curbelor de mișcare. Fie că este vorba de o bară glisantă, de o fereastră modală sau de un meniu derulant, adăugarea cantității potrivite de animație și făcându-l să arate neted și natural va crește foarte mult calitatea interfeței dvs. de utilizator. Va face ca interfața cu utilizatorul să se simtă bine. Luați meniul glisant de mai jos:

Făcând clic pe meniul de hamburger, apare meniul din stânga, dar animația pare blocată. Linia 51 din CSS arată că animația are transition-timing-function setată la linear . Putem îmbunătăți acest lucru. Să trecem la cubic-bezier și să creăm o funcție de sincronizare personalizată.

Dacă citiți acest lucru, este sigur să presupuneți că sunteți un designer sau un dezvoltator sau ambele și, prin urmare, nu sunteți străin de curbele cubice Bezier; sunt șanse mari să le fi întâlnit măcar o dată. Curbele Bezier sunt o minune. Ele sunt utilizate în principal în grafica computerizată pentru a desena forme și sunt utilizate în instrumente precum Sketch și Adobe Illustrator pentru a desena grafică vectorială. Motivul pentru care curbele cubice Bezier sunt atât de populare este că sunt atât de ușor de utilizat: trebuie doar să modificați pozițiile celor patru puncte diferite și să creați tipul de curbă de care aveți nevoie.

Deoarece știm întotdeauna stările inițiale și finale ale obiectului animat, putem fixa două dintre puncte. Mai rămân doar două puncte ale căror poziții trebuie să le modificăm. Cele două puncte fixe se numesc puncte de ancorare, iar cele două puncte rămase sunt puncte de control.

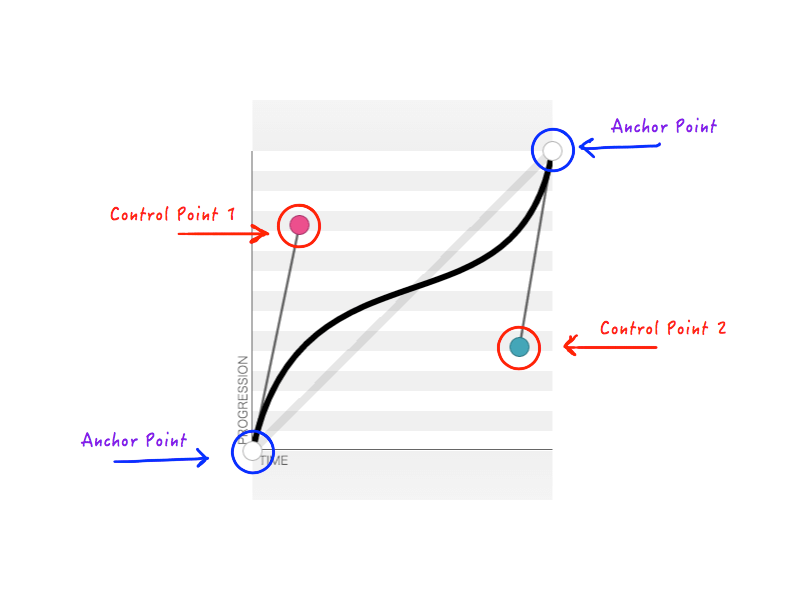
După cum vă amintiți, cubic-bezier acceptă patru numere ( n1, n2, n3, n4 ) atunci când creați o transition-timing-function . Aceste patru numere nu reprezintă altceva decât pozițiile celor două puncte de control: n1, n2 reprezintă coordonatele x și y ale primului punct de control, iar n3, n4 reprezintă coordonatele celui de-al doilea punct de control. Deoarece schimbarea poziției punctelor de control va schimba forma curbei și, prin urmare, animația noastră în ansamblu, rezultatul este același atunci când oricare sau toate dintre n1, n2, n3, n4 sunt modificate. De exemplu, figura de mai jos reprezintă cubic-bezier(.14, .78, .89, .35) :

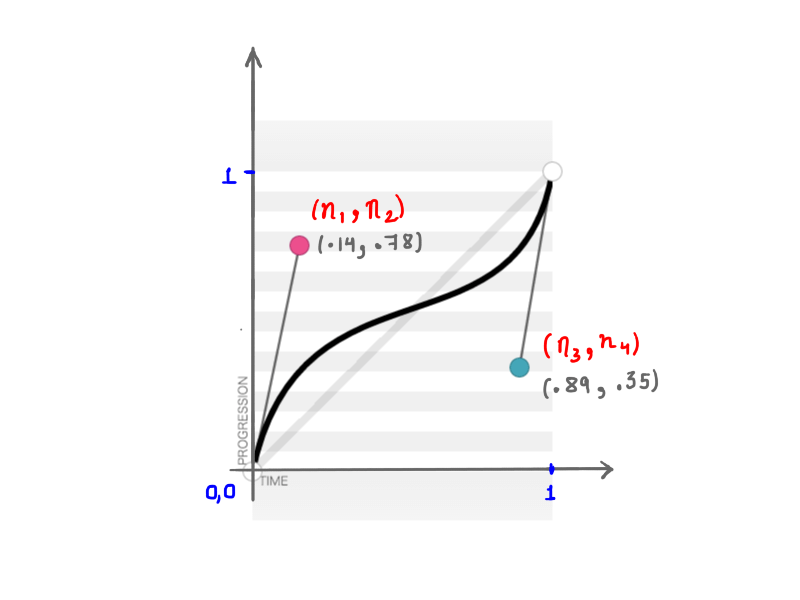
Matematica din spatele acestor curbe aparent simple este fascinantă.

În regulă, în regulă, să revenim la locul în care mergeam cu cubic-bezier: crearea unei transition-timing-function . Vreau genul de animație în care meniul alunecă foarte repede și apoi încetinește cu grație și se termină:

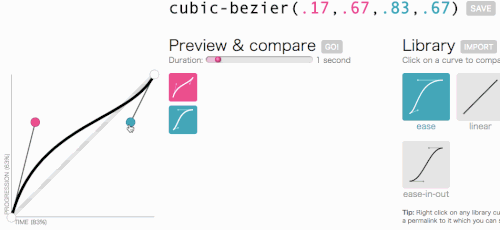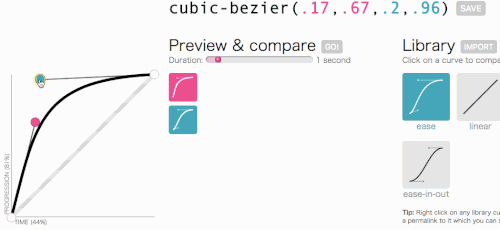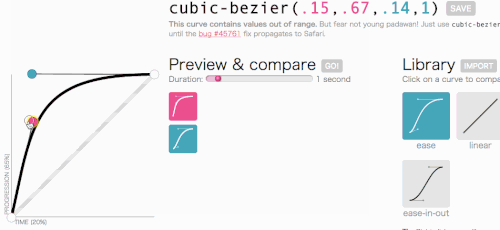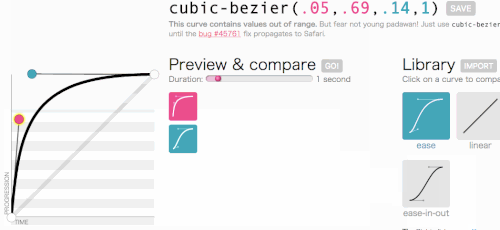
Asta arată bine. Animația va începe rapid și apoi va încetini, mai degrabă decât să se miște cu o viteză constantă. Pur și simplu o să copiez cubic-bezier(.05, .69, .14, 1) din partea de sus a paginii și să înlocuiesc linear cu acesta.

Vezi diferenta? A doua iterație pare mult mai naturală și atrăgătoare. Imaginează-ți dacă fiecare animație din interfața ta de utilizare ar urma o funcție de sincronizare naturală. Cât de grozav ar fi?

După cum am văzut, curbele de mișcare nu sunt deloc complicate. Sunt foarte ușor de înțeles și de folosit. Cu ele, îți poți duce interfața la următorul nivel.

Sper că ați învățat cum funcționează curbele de mișcare. Dacă treceai prin multe încercări și erori pentru ca curbele de mișcare să funcționeze așa cum ți-ai dori sau dacă nu le foloseai deloc, acum ar trebui să te simți confortabil să le îndoiești după voința ta și să creezi animații frumoase. Pentru că, până la urmă, animația contează.