Derivată de regulă în lanț în învățarea automată: explicată

Învățarea automată a evoluat pentru a deveni unul dintre cele mai discutate și mai cercetate domenii din anii actuali și din toate motivele întemeiate. Noi modele și aplicații ale învățării automate sunt descoperite în fiecare zi, iar cercetătorii din întreaga lume lucrează la următorul lucru important.

Drept urmare, a existat un interes crescut pentru profesioniștii din medii variate pentru a trece la învățarea automată și a fi parte a acestei revoluții în curs de desfășurare. Dacă sunteți unul dintre pasionații de învățare automată care doresc să facă primii pași, să vă spunem că începe cu înțelegerea elementelor de bază ale matematicii și statisticii înainte de orice altceva.

Un astfel de subiect vital în matematică care este foarte relevant pentru învățarea automată este derivatele. Din înțelegerea de bază a calculului, ți-ai aminti că derivata oricărei funcții este rata instantanee de modificare a acelei funcții. În acest blog, ne vom aprofunda în derivate și vom explora regula lanțului. Vom vedea cum se schimbă rezultatul unei anumite funcții atunci când modificăm unele variabile independente din ecuație. Cu cunoștințele derivate ale regulilor în lanț, veți putea lucra la diferențierea funcțiilor mai complexe pe care sigur le veți întâlni în învățarea automată.

Obțineți certificare de învățare automată online de la cele mai bune universități din lume – masterat, programe executive postuniversitare și program de certificat avansat în ML și AI pentru a vă accelera cariera.

Înțelegerea derivatei regulii lanțului

Regula lanțului este în esență o formulă matematică care vă ajută să calculați derivata unei funcții compuse. O funcție compusă este una care este compusă din două sau mai multe funcții. Deci, dacă f și g sunt două funcții, atunci regula lanțului ne-ar ajuta să găsim derivata funcțiilor compuse, cum ar fi fog sau go f.

Având în vedere funcția compozită ceață, iată cum ar arăta derivata regulii lanțului:

Regula de mai sus poate fi scrisă și ca:

Unde funcția F este compoziția lui f și g , sub forma f(g(x)).

Acum, să presupunem că avem trei variabile astfel încât a treia variabilă (z) depinde de a doua variabilă (y), care la rândul ei depinde de prima variabilă (x). În acest caz, derivata regulii lanțului ar arăta cam așa:

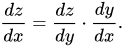În ceea ce privește învățarea profundă, aceasta este și formula utilizată în mod regulat pentru a rezolva problemele de backpropagation. Acum, din moment ce am menționat că z depinde de y și y de x, putem scrie z = f(y) și y = g(x). Această înlocuire ar modifica ecuația noastră diferențială în felul următor:

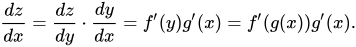Acum, să ne uităm la câteva exemple de derivate ale regulilor în lanț pentru a înțelege mai bine matematica din spatele lor.

Exemple și aplicații ale derivatelor regulii în lanț

Să luăm un exemplu binecunoscut de la Wikipedia pentru a înțelege mai bine derivata regulii în lanț. Să presupunem că faci o cădere liberă din cer. Presiunea atmosferică pe care o întâlnești în timpul toamnei se va schimba constant. Iată un grafic care prezintă această modificare a presiunii atmosferice cu nivelurile de altitudine:

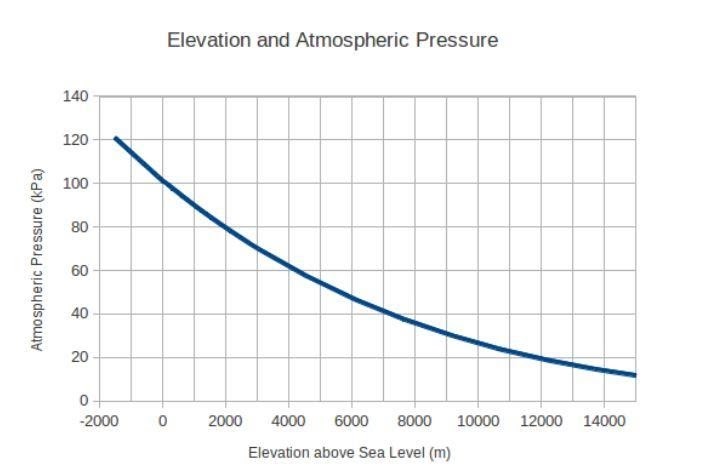
Să presupunem că căderea a început la 4000 de metri deasupra nivelului mării. Inițial, viteza ta a fost zero, iar valoarea accelerației a fost de 9,8 metri pe secundă pătrat din cauza gravitației.

Acum, să comparăm această situație cu metoda anterioară a regulii lanțului. În acest exemplu, vom folosi variabila „t” pentru timp în loc de x.

Apoi, variabila y = g(t), care spune distanța parcursă de la începutul căderii, poate fi dată ca:

g(t) = 0,5*9,8t^2

Și, înălțimea de la nivelul mării poate fi dată de o variabilă „h”, care va fi egală cu 400-g(t).

Să presupunem că, pe baza unui model, putem scrie și funcția presiunii atmosferice la orice înălțime h ca:

f(h) = 101325 e−0,0001h

Acum, puteți distinge între cele două ecuații pe baza variabilelor lor dependente pentru a obține următoarele rezultate:

g′(t) = −9,8t,

Aici, g'(t) spune valoarea vitezei tale în orice moment t.

f′(h) = −10,1325e−0,0001h

Aici, f′(h) este viteza de modificare a presiunii atmosferice în raport cu înălțimea h. Acum, întrebarea este: putem combina aceste două ecuații și putem deduce rata de schimbare a presiunii atm în funcție de timp? Să vedem folosind regula lanțului:

Ecuația finală pe care o avem ne oferă viteza de schimbare a presiunii atmosferice în raport cu timpul trecut de la toamnă. În ceea ce privește învățarea automată, rețelele neuronale au nevoie în mod constant de actualizări de greutate cu privire la eroarea neuronului în predicție. Regula lanțului ajută la ajustarea acestor greutăți și aduce modelul de învățare automată mai aproape de rezultatul corect.

Concluzie

După cum puteți vedea, regula lanțului este benefică în multe scopuri. Mai ales când vine vorba de învățarea automată sau învățarea profundă, regula lanțului își găsește o mulțime de utilizare în actualizarea greutăților neuronilor și îmbunătățirea eficienței generale a modelului.

Acum că ești conștient de elementele de bază ale regulii lanțului, continuă și încearcă singur câteva probleme. Căutați câteva funcții compuse și încercați să găsiți derivatele lor. Cu cât exersezi mai mult, cu atât conceptele tale vor deveni mai clare și cu atât îți va fi mai ușor să-ți antrenezi modelele de învățare automată! Acestea fiind spuse, dacă ești un pasionat de învățare automată, dar te străduiești să faci primii pași în acest domeniu, upGrad te sprijină!

Programul nostru Executive PG în Machine Learning și AI este oferit în colaborare cu IIIT-Bangalore și vă oferă posibilitatea de a alege dintre șase specializări relevante pentru industrie. Cursul începe de la nivelul solului și vă duce la vârf, oferindu-vă în același timp sprijin individual din partea experților din industrie, un grup puternic de studenți și sprijin în carieră la 360 de grade.