Distribuție binomială în Python cu exemple din lumea reală [2022]

Valoarea probabilității și a statisticilor în domeniul științei datelor a fost imensă, inteligența artificială și învățarea automată bazându-se în mare măsură pe acestea. Folosim modele de proces de distribuție normală de fiecare dată când efectuăm teste A/B și modelări de investiții.

Cu toate acestea, distribuția binomială în Python este aplicată în mai multe moduri pentru a efectua mai multe procese. Dar, înainte de a începe cu distribuția binomială în Python , trebuie să știți despre distribuția binomială în general și despre utilizarea acesteia în viața de zi cu zi. Dacă sunteți începător și doriți să aflați mai multe despre știința datelor, consultați formarea noastră în știința datelor de la universități de top.

Ce este distribuția binomială ?

Ai aruncat vreodată o monedă? Dacă ai, atunci trebuie să știi despre probabilitatea de a obține cap sau cozi este egală. Dar, ce zici de probabilitatea de a obține șapte cozi în total zece aruncări de monedă? Aici distribuția binomială poate ajuta la calcularea rezultatelor fiecărei aruncări și, astfel, la aflarea probabilității de a obține șapte cozi pentru zece aruncări ale unei monede.

Cheia distribuției probabilităților provine din varianța oricărui eveniment. Pentru fiecare set de zece aruncări de monede, probabilitatea de a obține cap și cozi poate fi oriunde între una și zece ori, egal și probabil. Incertitudinea rezultatului (cunoscută și ca varianță) ajută la generarea distribuției rezultatelor produse.

Cu alte cuvinte, distribuția binomială este un proces în care există doar două rezultate posibile: adevărat sau fals. Prin urmare, are o probabilitate egală pentru ambele rezultate pentru toate evenimentele, deoarece aceleași acțiuni sunt efectuate de fiecare dată. Există o singură condiție... Pașii trebuie să fie complet neafectați unul de celălalt, iar rezultatele pot fi sau nu la fel de probabile.

Prin urmare, funcția de probabilitate a unei distribuții binomiale este:

f f( k k , n n, p p) = P r Pr( k k; n n, p p) = P r Pr ( X X= k k) =

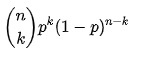
Sursă

Unde,

= n n! k k !( n n!- k k!)

Aici, n = numărul total de încercări

p = probabilitatea de succes

k = numărul țintă de succese

Distribuție binomială în Python

Pentru distribuția binomială prin Python, puteți produce variabila aleatoare distinctă din funcția binom.rvs (), unde „n” este definit ca frecvența totală a încercărilor, iar „p” este egal cu probabilitatea de succes.

De asemenea, puteți muta distribuția folosind funcția loc, iar dimensiunea definește frecvența unei acțiuni care se repetă în serie. Adăugarea unui random_state poate ajuta la menținerea reproductibilității.

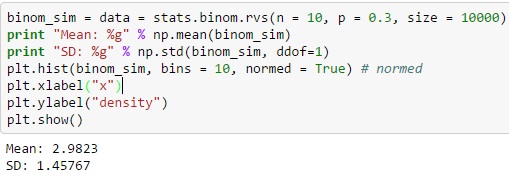
Sursă

Exemple reale de distribuție binomială în Python

Există mult mai multe evenimente (mai mari decât aruncările de monede) care pot fi abordate prin distribuția binomială în Python. Unele dintre cazurile de utilizare pot ajuta la urmărirea și îmbunătățirea rentabilității investițiilor (rentabilitatea investițiilor) pentru companiile mari și mici. Iată cum:

• Gândiți-vă la un centru de apeluri în care fiecare angajat primește în medie 50 de apeluri în fiecare zi.
• Probabilitatea de conversie pentru fiecare apel este egală cu 4%.
• Venitul mediu generat de companie pe baza fiecărei astfel de conversii este de 20 USD.
• Dacă analizezi 100 de astfel de angajați, care sunt plătiți cu 200 USD în fiecare zi, atunci

n = 50

p = 4%

Codul poate genera rezultate după cum urmează:

• Rata medie de conversie pentru fiecare angajat = 2,13
• Abaterea standard a conversiilor pentru fiecare personal din call center = 1,48
• Conversie brută = 213
• Generare de venituri brute = 21.300 USD
• Cheltuială brută = 20.000 USD
• Profit brut = 1.300 USD

Modelele de distribuție binomială și alte distribuții de probabilitate pot prezice doar o aproximare care se poate apropia de lumea reală în ceea ce privește parametrii de acțiune, „n” și „p”. Ne ajută să înțelegem și să identificăm domeniile noastre de interes și să îmbunătățim șansele generale de performanță și eficacitate mai bune.

Citește și: 13 idei și subiecte interesante de proiecte cu structură de date pentru începători

Ce urmează?

Dacă sunteți curios să aflați despre știința datelor, consultați programul Executive PG în știința datelor de la IIIT-B și upGrad, care este creat pentru profesioniști care lucrează și oferă peste 10 studii de caz și proiecte, ateliere practice practice, mentorat cu experți din industrie, 1 -on-1 cu mentori din industrie, peste 400 de ore de învățare și asistență profesională cu firme de top.