Arborele binar vs Arborele de căutare binar: Diferența dintre Arborele binar și Arborele de căutare binar
Publicat: 2021-01-21Cuprins
Introducere
Sortarea este procesul de aranjare a datelor într-o ordine sistematică, astfel încât să poată fi analizate mai eficient. Procesul de identificare a unei anumite înregistrări se numește căutare. Dacă datele sunt sortate corect într-o anumită ordine, atunci căutarea devine o sarcină ușoară și eficientă. Acest articol tratează una dintre cele mai importante structuri de date neliniare, adică arborii.
Arborii sunt utilizați în primul rând pentru a reprezenta date prin demonstrarea unei relații ierarhice între elemente. De exemplu, cuprins, arbore genealogic. Din punct de vedere tehnic, un arbore poate fi definit ca o mulțime finită „T” a unuia sau mai multor noduri, astfel încât un nod este atribuit ca rădăcină a arborelui, iar celelalte noduri sunt împărțite în n>=0 seturi disjunse T1, T2, T3, T4... Tn și sunt numite subarbori sau copii ai acelui nod rădăcină.
Ce este un arbore binar?
Un arbore binar este o structură de date neliniară în care un nod poate avea fie 0, 1 sau 2 noduri. Fiecare nod din arborele binar este denumit fie un nod părinte, fie ca un nod copil. Nodul cel mai de sus al Arborelui Binar este denumit nodul rădăcină. Fiecare nod părinte poate avea cel mult 2 noduri copil care sunt nodul copil stâng și nodul copil drept.
Un nod dintr-un arbore binar are trei câmpuri:
- Element de date – Stochează valoarea datelor care urmează să fie stocată de nod.
- Pointer la copilul din stânga – Stochează referința (sau adresa) la nodul copil din stânga.
- Pointer către copilul din dreapta – Stochează referința la nodul din dreapta.
În acest fel, mai multe noduri sunt combinate împreună pentru a construi un Arbore Binar.
Un arbore binar poate fi reprezentat astfel:
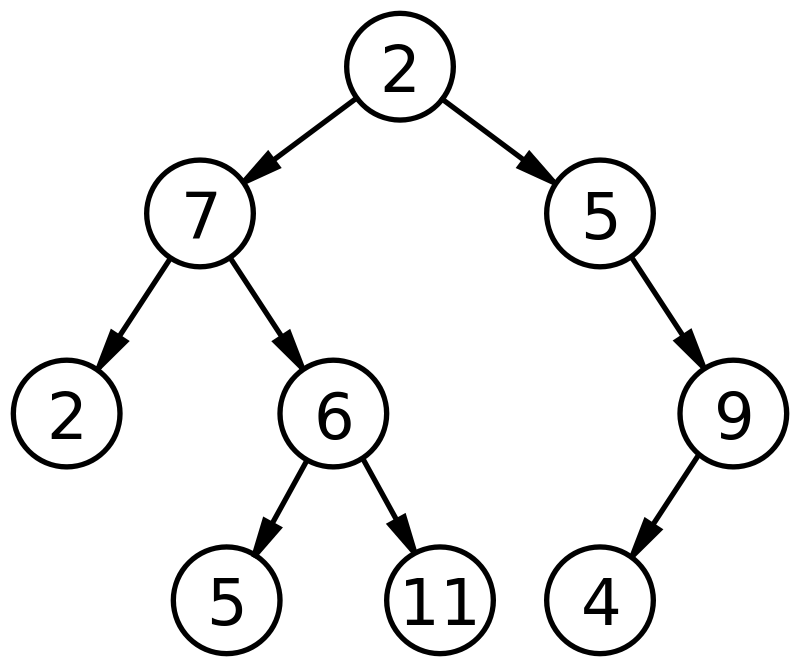
Sursă
Din figura de mai sus, nodul rădăcină 2 are doi copii (sau noduri copil), 7 și 5. 7 este denumit nodul copil stâng și 5 este numit nodul copil dreapta. În acest fel, fiecare dintre nodurile copil acționează ca un nod părinte pentru mai multe alte noduri și împreună reprezintă Arborele Binar.
Verificați: Tipuri de arbore binar
Terminologii utilizate în Arborele Binar
Nod : Reprezentarea de bază a unui punct de terminare într-un arbore.
Nodul rădăcină : cel mai înalt nod al unui arbore binar.
Nod părinte : Dacă un nod este conectat la un alt nod prin margini, este cunoscut ca nod părinte. Într-un arbore binar, un nod părinte poate avea maximum 2 noduri-fii.
Nod copil : Dacă un nod are un predecesor, acesta este cunoscut ca nod copil.
Nod frunză : un nod care nu are niciun nod copil este numit nod frunză.
Adâncimea unui nod : este distanța de la nodul rădăcină la acel nod particular a cărui adâncime urmează să fie măsurată.
Înălțimea arborelui : este cea mai mare distanță de la nodul rădăcină la nodul frunzei.
Acestea sunt câteva terminologii de bază ale unui arbore binar. Cu această înțelegere de bază a unui arbore binar, să trecem la o avansare a arborelui binar cunoscut sub numele de arbore de căutare binar.
Citește și: Algoritmul de căutare binar: funcție, beneficii, complexitate timp și spațiu
Ce este un arbore binar de căutare
După cum sugerează și numele, un arbore de căutare binar sau BST este un arbore care este utilizat pentru sortarea, preluarea și căutarea datelor. Este, de asemenea, un tip de structură de date neliniară în care nodurile sunt aranjate într-o anumită ordine. Prin urmare, este numit și „ Arborele binar ordonat ”. Are următoarele proprietăți:
- Subarborele din stânga al unui nod are noduri care sunt doar mai mici decât cheia nodului respectiv.
- Subarborele din dreapta al unui nod are noduri care sunt doar mai mari decât cheia acelui nod.
- Fiecare nod are chei distincte și duplicatele nu sunt permise în Arborele de căutare binar.
- Subarborele din stânga și din dreapta trebuie să fie, de asemenea, un arbore de căutare binar.
Să vizualizăm acest concept pentru a obține o înțelegere clară a arborilor de căutare binari.
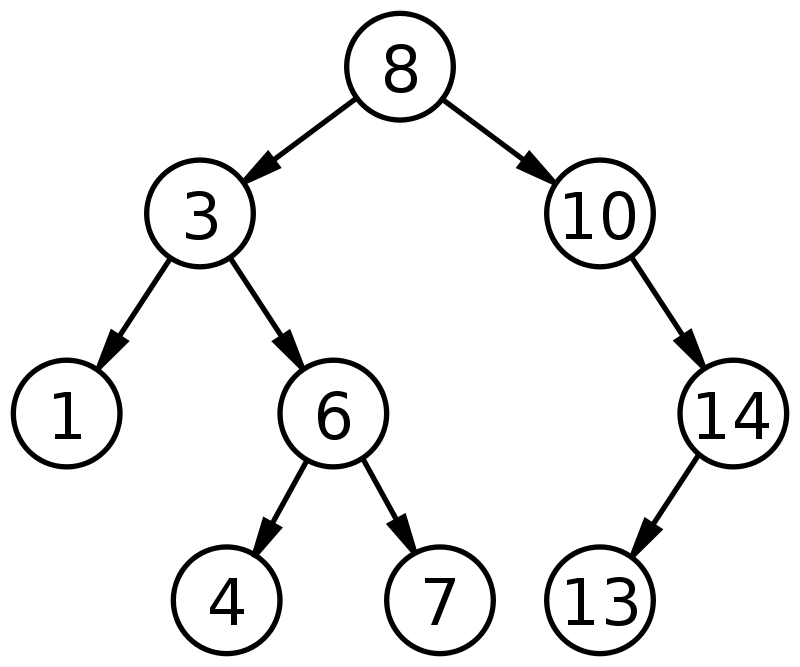
Sursă
În figura de mai sus, vedem că valoarea nodului rădăcină este 8. Cu o analiză suplimentară, se observă că toate valorile din subarborele din stânga sunt mai mici decât valoarea nodului rădăcină și toate valorile din subarborele din dreapta au valori care sunt mai mari decât nodul rădăcină. În plus, se observă că fiecare valoare din Arborele de căutare binar este unică și nu există duplicate. Astfel, proprietățile Arborelui de căutare binar menționate mai sus sunt verificate.
Într-un alt exemplu, vedem că, deși subarborele din stânga și din dreapta sunt arbori de căutare binari cu valori unice în întreg arborele. Valoarea la nodul frunză din subarborele din stânga este 12, care este mai mare decât valoarea nodului rădăcină, care este 12. Astfel, aceasta nu satisface proprietatea BST și, prin urmare, nu este un Arbore de căutare binar.
Operațiune de căutare într-un BST –
Luați în considerare un arbore de căutare binar cu valorile date mai jos. Să înțelegem cum se efectuează operația de căutare pentru a obține 9 din Arborele de căutare binar.

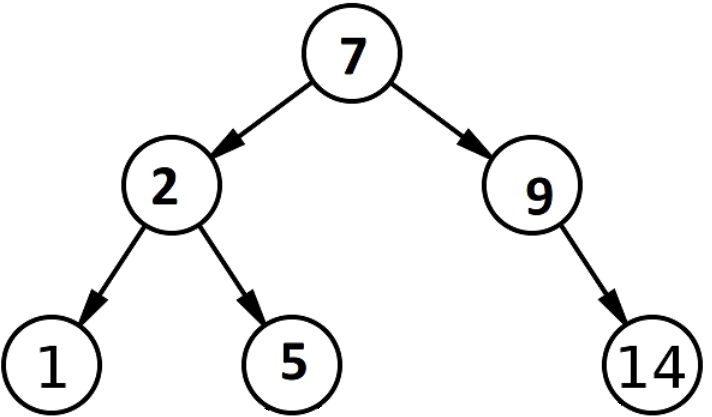
Sursă
Pentru a efectua căutarea binară, inițial vom aranja toate numerele întregi într-un tablou sortat. Acesta se numește spațiu de căutare. Acest spațiu de căutare va consta din doi pointeri, numiți pointeri de început și de final. Matricea arborelui de căutare binar dat de mai sus este reprezentată ca:
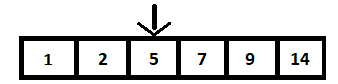
Primul pas este să calculăm valoarea medie a matricei și să o comparăm cu valoarea care urmează să fie căutată, 9 în cazul nostru. Acest lucru se face prin calcularea n/2, unde n este numărul total de elemente din matrice (BST) și este 6. Astfel, al treilea element este elementul din mijloc care este 5.
Acum că elementul din mijloc este comparat cu 9 și deoarece nu este egal (mai mare), operația de căutare va fi efectuată pe tabloul din dreapta. În acest fel, operația de căutare este redusă la jumătate, după cum se arată mai jos:
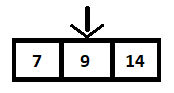
În pasul următor, elementul din mijloc este calculat și se constată că este 9, ceea ce se potrivește cu elementul nostru de căutat.
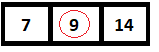
Arborele binar vs Arborele de căutare binar –
Acum că avem o înțelegere de bază atât despre Arborele binar, cât și despre Arborele de căutare binar, haideți să rezumam rapid unele dintre diferențele dintre ambele.
| Baza pentru comparație | Arborele binar | Arborele de căutare binar |
| Definiție | Un arbore binar este o structură de date neliniară în care un nod poate avea 0, 1 sau 2 noduri. Individual, fiecare nod constă dintr-un indicator stânga, un indicator din dreapta și un element de date. | Un arbore binar de căutare este un arbore binar organizat cu o organizare structurată a nodurilor. Fiecare subarbore trebuie să aibă, de asemenea, acea structură particulară. |
| Structura | Nu există nicio structură de organizare necesară a nodurilor din arbore. | Valorile subarborelui din stânga unui anumit nod ar trebui să fie mai mici decât nodul respectiv, iar valorile subarborelui din dreapta ar trebui să fie mai mari. |
| Operațiuni efectuate | Operațiile care pot fi efectuate sunt ștergerea, inserarea și parcurgerea | Deoarece aceștia sunt arbori binari sortați, ei sunt utilizați pentru căutarea, inserarea și ștergerea rapidă și eficientă a binarelor. |
| Tipuri | Există mai multe tipuri. Cele mai comune sunt Arborele Binar Complet, Arborele Binar Complet, Arborele Binar Extins | Cele mai populare sunt AVL Trees, Splay Trees, Tango Trees, T-Trees. |
Concluzie
Astfel, deducem că, deși atât Arborele binar, cât și Arborele de căutare binar au o structură ierarhică comună cu o colecție de noduri, ele au mai multe diferențe în aplicarea lor. Un arbore binar este o structură de bază cu o regulă simplă că niciun părinte nu trebuie să aibă mai mult de 2 copii, în timp ce arborele binar de căutare este o variantă a arborelui binar urmând o anumită ordine în care ar trebui organizate nodurile.
Dacă sunteți curios să aflați despre Arborele binar vs Arborele de căutare binar, consultați Diploma PG în știința datelor de la IIIT-B și upGrad, care este creată pentru profesioniști care lucrează și oferă peste 10 studii de caz și proiecte, ateliere practice practice, mentorat cu industrie experți, 1-la-1 cu mentori din industrie, peste 400 de ore de învățare și asistență la locul de muncă cu firme de top.
Învață cursuri de știință a datelor online de la cele mai bune universități din lume. Câștigă programe Executive PG, programe avansate de certificat sau programe de master pentru a-ți accelera cariera.
Cum putem traversa un arbore binar de căutare?
Spre deosebire de structurile de date liniare, cum ar fi matrice, liste legate, stive și cozi, în care putem traversa structura de date doar într-un singur mod, un arbore binar de căutare ne oferă libertatea de a o traversa în mai multe moduri. Cele mai populare traversări ale arborelui sunt următoarele: într-o traversare în ordine, mai întâi parcurgem nodul din stânga al arborelui, apoi nodul rădăcină al arborelui și, în final, nodul din dreapta al arborelui. Urmăm aceeași modă și în toți subarborele. Într-o traversare în precomandă, parcurgem mai întâi nodul rădăcină al arborelui și apoi nodul din stânga și respectiv din dreapta. Urmăm aceeași modă și în toți subarborele. Într-o traversare post-comandă, mai întâi parcurgem nodul din stânga și respectiv din dreapta al arborelui și, în final, nodul rădăcină al arborelui. Urmăm aceeași modă și în toate subarborele.
Care sunt avantajele și dezavantajele unui BST?
Următoarele sunt avantajele și dezavantajele unui arbore de căutare binar. Avantajele sunt - Operațiuni precum inserarea, ștergerea și căutarea pot fi efectuate în timp O(log n) unde n este numărul de noduri. Toate elementele dintr-un BST sunt sortate astfel încât să putem traversa cu ușurință printr-un BST folosind pur și simplu traversarea în ordine. BST poate fi utilizat eficient pentru a proiecta alocatoare de memorie pentru a accelera procesul de căutare a blocurilor de memorie. Cel mai mare dezavantaj al unui arbore de căutare binar este că trebuie să folosim întotdeauna un BST echilibrat, cum ar fi AVL și arborele roșu-negru, deoarece dacă nu folosim un BST echilibrat, operațiunile noastre în arbore nu vor fi efectuate în timp logaritmic.
Faceți diferența între un arbore binar complet și un arbore binar complet.
Un arbore binar complet este un arbore binar în care toate nodurile au noduri copii între 0 și 2. Cu alte cuvinte, un arbore binar în care toate nodurile au cel puțin 2 noduri copii, cu excepția nodurilor frunze, este cunoscut ca arbore binar complet. Pe de altă parte, un arbore binar complet este un arbore binar în care fiecare nod este complet umplut (exact două noduri copii) și nodurile frunzelor sunt situate cât mai stânga posibil.
