Statistica Bayesiană și modelul: explicat

Tehnica bayesiană este o abordare în statistică utilizată în analiza datelor și estimarea parametrilor. Această abordare se bazează pe teorema Bayes.

Statistica Bayesiană urmează un principiu unic în care ajută la determinarea distribuției comune a probabilității pentru parametrii observați și neobservați folosind un model statistic. Cunoașterea statisticilor este esențială pentru a aborda problemele analitice în acest scenariu.

Încă de la introducerea teoremei Bayes în anii 1770 de către Thomas Bayes, aceasta a rămas un instrument indispensabil în statistică. Modelele bayesiene sunt un înlocuitor clasic pentru modelele frecventiste, deoarece inovațiile recente în statistică au ajutat la depășirea reperelor într-o gamă largă de industrii, inclusiv cercetarea medicală, înțelegerea căutărilor pe web și procesarea limbilor naturale (Procesarea limbajului natural).

De exemplu, Alzheimer este o boală cunoscută că prezintă un risc progresiv pe măsură ce o persoană îmbătrânește. Cu toate acestea, cu ajutorul teoremei Bayes, medicii pot estima probabilitatea ca o persoană să aibă Alzheimer în viitor. De asemenea, se aplică cancerului și altor boli legate de vârstă la care o persoană devine vulnerabilă în ultimii ani ai vieții sale.

Statistici frecvente vs statistici bayesiene

Statistici frecvente vs statisticile bayesiene a fost în mod constant un subiect de controversă și coșmaruri pentru începători, ambii având dificultăți în a alege între cele două. La începutul secolului al XX-lea, statistica bayesiană a suferit cota sa de probleme de neîncredere și acceptare. Cu timpul, totuși, oamenii și-au dat seama de aplicabilitatea modelelor bayesiene și de soluțiile exacte pe care le oferă.

Iată, aruncăm o privire asupra statisticilor frecvente și a complexităților asociate cu acestea:

Statistici frecvente

Este o metodologie inferenţială utilizată pe scară largă în lumea statisticii. Acesta analizează dacă a avut loc sau nu un eveniment (menționat ca ipoteză). De asemenea, estimează probabilitatea ca evenimentul să se producă în timpul experimentului. Experimentul se repetă până când se obține rezultatul dorit.

Eșantioanele de distribuție ale acestora sunt de dimensiune reală, iar experimentul se repetă de infinite ori teoretic. Iată un exemplu care arată cât de des pot fi folosite statisticile pentru a studia aruncarea unei monede.

• Posibilitatea de a obține un cap la aruncarea monedei o dată este de 0,5 (1/2).
• Numărul de capete indică numărul real de lead-uri obținute.
• Diferența dintre numărul real de capete și numărul așteptat de capete va crește pe măsură ce crește numărul de aruncări.

Deci, aici, rezultatul depinde de numărul de ori se repetă experimentul. Este un dezavantaj major al statisticilor frecvente.

Alte defecte asociate cu tehnicile sale de proiectare și interpretare au devenit evidente în secolul al XX-lea, când aplicarea statisticilor frecvente la modelele numerice a fost la apogeu.

Limitările statisticilor frecvente

Cele trei defecte majore ale statisticilor frecvente sunt enumerate mai jos:

1. Valorile p variabilei

Valorile lui p măsurate pentru un eșantion cu o dimensiune fixă ​​într-un experiment cu un punct final definit se modifică cu orice modificare a punctului final și a dimensiunii eșantionului. Rezultă două valori p pentru o singură dată care este incorectă.

2. Intervale inconsecvente de încredere

CI (Intervalul de încredere) depinde numai de dimensiunea eșantionului. Face potențialul de oprire irelevant.

3. Valorile estimate ale CI

Intervalele de încredere nu sunt o distribuție de probabilitate, iar valorile lor pentru un parametru sunt doar o estimare și nu valori reale.

Cele trei motive de mai sus au dat naștere abordării bayesiene care aplică probabilități problemelor statistice.

Nașterea statisticii bayesiene

Reverendul Thomas Bayes a propus pentru prima dată abordarea bayesiană a statisticii în eseul său scris în 1763. Această abordare a fost publicată de Richard Price ca o strategie în probabilitate inversă pentru a prognoza evenimentele viitoare bazate pe trecut.

Abordarea se bazează pe teorema Bayes, care este explicată mai jos:

Teorema lui Bayes

Axioma probabilității lui Renyi examinează probabilitățile condiționate, unde posibilitățile de apariție a evenimentului A și B sunt dependente sau condiționate. Probabilitatea condițională de bază poate fi scrisă astfel:

Probabilitatea ca evenimentul B să se producă depinde de evenimentul A.

Ecuația de mai sus este fundamentul regulii Bayes, o expresie matematică a teoremei Bayes care afirmă:

Aici, ∩ denotă intersecția.

Regula Bayes poate fi scrisă astfel:

Regula Bayes este fundamentul statisticii bayesiene, în care informațiile disponibile despre un anumit parametru dintr-un model statistic sunt comparate și actualizate cu datele colectate.

Cunoștințele de bază sunt reprezentate ca distribuție anterioară, care este apoi comparată și studiată cu datele observate sau colectate ca funcție de probabilitate pentru a afla distribuția posterioară.

Această distribuție posterioară este folosită pentru a face predicții despre evenimente viitoare.

Aplicațiile abordării bayesiene depind de următorii parametri:

1. Definirea modelului anterior și de date
2. Efectuarea de inferențe relevante
3. Analiza si eficientizarea modelelor

Ce sunt rețelele neuronale bayesiene?

Rețelele neuronale bayesiene (BNN) sunt rețele pe care le creați atunci când extindeți rețelele standard utilizând metodologia statistică și modificați inferența posterioară pentru a urmări supraadaptarea. Deoarece este o abordare bayesiană, există o distribuție de probabilitate asociată cu parametrii rețelelor neuronale.

Sunt folosite pentru a rezolva probleme complexe în care nu există un flux liber de date disponibil. Rețelele neuronale bayesiene ajută la controlul supraajustării în domenii precum biologia moleculară și diagnosticul medical.

Se poate lua în considerare o întreagă distribuție de răspunsuri la o întrebare, mai degrabă decât o singură posibilitate folosind rețele neuronale bayesiene. Ele vă ajută să determinați selecția/compararea modelului și să abordați problemele care implică regularizarea.

Statistica bayesiană oferă instrumente matematice pentru a raționaliza și actualiza cunoștințele subiective referitoare la date noi sau dovezi științifice. Spre deosebire de abordarea statistică frecventă, aceasta funcționează pe baza presupunerii că probabilitățile depind de frecvența evenimentelor care se repetă în aceleași condiții.

Pe scurt, tehnica bayesiană este o extensie a presupunerii și opiniilor unui individ. Aspectul cheie al modelului bayesian care îl face mai eficient este înțelegerea că indivizii diferă în opinii în funcție de tipul de informații pe care le primesc.

Cu toate acestea, pe măsură ce apar noi dovezi și date, indivizii au un punct de convergență, inferența bayesiană . Această actualizare rațională este caracteristica specială a statisticii bayesiene care o face mai eficientă în problemele analitice.

Aici, probabilitatea de 0 se aplică atunci când nu există nicio speranță pentru un eveniment, iar probabilitatea de 1 se aplică atunci când este sigur că evenimentul va avea loc. O probabilitate între 0 și 1 oferă loc pentru alte rezultate potențiale.

Regula Bayes este acum aplicată pentru a obține inferența bayesiană pentru a obține o inferență mai bună din model.

Cum aplicați regula Bayes pentru a obține inferența bayesiană?

Luați în considerare ecuația:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) denotă distribuția anterioară,

P(θ|D) denotă credința posterioară,

P(D) reprezintă dovezile,

P(D|θ) indică probabilitatea.

Obiectivul principal al inferenței bayesiene este de a oferi o metodă rațională și precisă din punct de vedere matematic pentru îmbinarea credințelor cu dovezi pentru a obține credințe posterioare actualizate. Credințele posterioare pot fi folosite ca credințe anterioare atunci când sunt generate noi date. Astfel, inferența bayesiană ajută la actualizarea continuă a credințelor cu ajutorul regulii lui Bayes.

Luând în considerare același exemplu de aruncare a monedelor, modelul bayesian actualizează procedura de la credințele dinainte spre cele posterioare cu noi răsturnări de monede. Metoda bayesiană oferă următoarele probabilități.

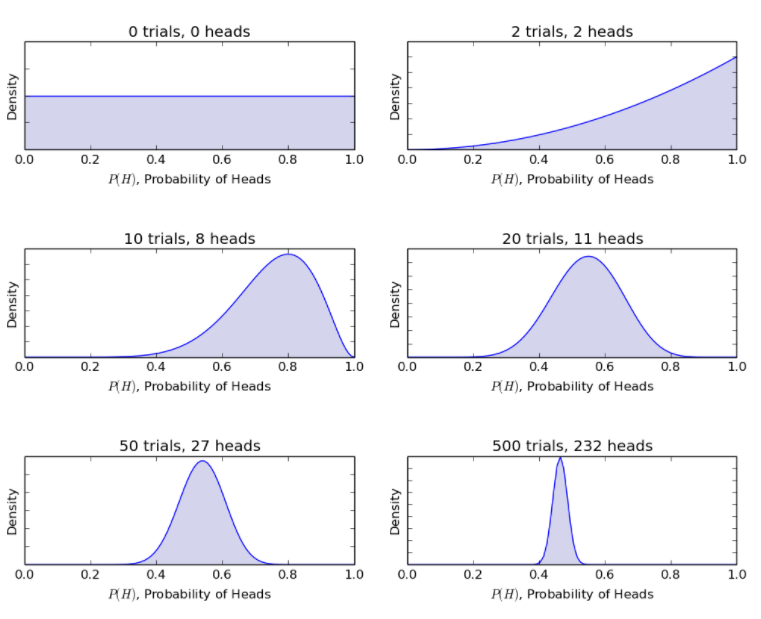
Sursă

Astfel, modelul bayesian permite raționalizarea unui scenariu incert cu informații restrânse la un scenariu mai definit cu o cantitate considerabilă de date.

Diferențe notabile între modelul bayesian și modelul frecventist

Statistici frecvente

Statistica bayesiană

Scopul este considerat ca o estimare punctuală și CI

Scopul este considerat ca o distribuție posterioară

Procedura pleacă de la observații

Procesul începe de la distribuția anterioară

Ori de câte ori se fac observații noi, abordarea frecventistă recalculează modelul existent.

Ori de câte ori se fac observații noi, distribuția posterioară (ideologie/ipoteză) este actualizată

Exemple: Estimarea mediei, testului t și ANOVA.

Exemple: Estimarea distribuției posterioare a mediei și suprapunerea intervalelor de mare densitate.

Avantajele statisticii bayesiene

• Oferă un mijloc organic și simplu de a combina informațiile preconcepute cu un cadru solid cu dovezi științifice. Informațiile trecute despre un parametru pot fi folosite pentru a forma o distribuție anterioară pentru investigații viitoare. Deducerile aderă la teorema Bayes.
• Inferențe dintr-un model bayesian sunt logice și precise din punct de vedere matematic și nu presupuneri brute. Precizia rămâne constantă indiferent de mărimea probei.
• Statisticile bayesiene urmează principiul probabilității. Când două eșantioane diferite au o funcție de probabilitate comună pentru o credință θ, toate inferențe despre credință ar trebui să fie similare. Tehnicile statistice clasice nu urmează principiul probabilității.
• Soluțiile dintr-o analiză bayesiană pot fi interpretate cu ușurință.
• Oferă o platformă favorabilă pentru diverse modele, cum ar fi modele ierarhice și probleme de date incomplete. Calculele tuturor modelelor parametrice pot fi urmărite virtual cu ajutorul altor tehnici numerice.

Aplicații de succes ale modelelor bayesiene de-a lungul istoriei

Metodele bayesiene au avut o mulțime de aplicații de succes în timpul celui de-al Doilea Război Mondial. Câteva dintre ele sunt enumerate mai jos:

• Un statistician rus, Andrey Kolmogorov , a folosit cu succes metode bayesiene pentru a îmbunătăți eficiența artileriei ruse.
• Modelele bayesiene au fost folosite pentru a sparge codurile bărcilor U germane.
• Un matematician american de origine franceză, Bernard Koopman, i-a ajutat pe aliați să identifice locația ambarcațiunilor U germane cu ajutorul modelelor bayesiene pentru a intercepta transmisiile radio.

Dacă doriți să aflați mai multe despre statisticile bayesiene, iată Certificarea avansată upGrad în învățare automată și cloud pentru a înțelege conceptele de bază prin proiecte din industrie și studii de caz din viața reală. Cursul de 12 luni este oferit de IIT Madras și sprijină învățarea în ritm propriu.

Contactați-ne pentru mai multe detalii.