Teorema Bayes explicată cu un exemplu – Ghid complet

Introducere

Ce este teorema Bayes?

Teorema lui Bayes este folosită pentru calcularea unei probabilități condiționate în care intuiția eșuează adesea. Deși folosită pe scară largă în probabilitate, teorema este aplicată și în domeniul învățării automate. Utilizarea sa în învățarea automată include adaptarea unui model la un set de date de antrenament și dezvoltarea modelelor de clasificare.

Ce este probabilitatea condiționată?

O probabilitate condiționată este de obicei definită ca probabilitatea unui eveniment având în vedere apariția unui alt eveniment.

• Dacă A și B sunt două evenimente, atunci probabilitatea condiționată me va fi desemnată ca P(A dat B) sau P(A|B).
• Probabilitatea condiționată poate fi calculată din probabilitatea comună (A | B) = P(A, B) / P(B)

• Probabilitatea condiționată nu este simetrică; De exemplu P(A | B) != P(B | A)

Alte modalități de calculare a probabilității condiționate includ utilizarea celeilalte probabilități condiționate, de ex

P(A|B) = P(B|A) * P(A) / P(B)

Se folosește și reversul

P(B|A) = P(A|B) * P(B) / P(A)

Acest mod de calcul este util atunci când este dificil să se calculeze probabilitatea comună. În rest, atunci când probabilitatea condiționată inversă este disponibilă, calculul prin aceasta devine ușor.

Acest calcul alternativ al probabilității condiționate este denumit Regula Bayes sau Teorema Bayes. Este numit sub persoana care a descris-o prima dată, „Reverendul Thomas Bayes”.

Teorema formulei lui Bayes

Teorema Bayes este o modalitate de a calcula probabilitatea condiționată atunci când probabilitatea comună nu este disponibilă. Uneori, numitorul nu poate fi accesat direct. În astfel de cazuri, modalitatea alternativă de calcul este următoarea:

P(B) = P(B|A) * P(A) + P(B|nu A) * P(nu A)

Aceasta este formularea teoremei Bayes care arată un calcul alternativ al lui P(B).

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|nu A) * P(nu A)

Formula de mai sus poate fi descrisă cu paranteze în jurul numitorului

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|nu A) * P(nu A))

De asemenea, dacă avem P(A), atunci P(nu A) poate fi calculat ca

P(nu A) = 1 – P(A)

În mod similar, dacă avem P(nu B|nu A), atunci P(B|nu A) poate fi calculat ca

P(B|nu A) = 1 – P(nu B|nu A)

Teorema Bayes a probabilității condiționate

Teorema Bayes constă din mai mulți termeni ale căror nume sunt date pe baza contextului aplicării sale în ecuație.

Probabilitatea posterioară se referă la rezultatul lui P(A|B), iar probabilitatea anterioară se referă la P(A).

• P(A|B): Probabilitate posterior.
• P(A): Probabilitate anterioară.

În mod similar, P(B|A) și P(B) sunt denumite probabilitate și dovezi.

• P(B|A): Probabilitate.
• P(B): Dovezi.

Prin urmare, teorema Bayes a probabilității condiționate poate fi reformulată astfel:

Posterior = Probabilitate * Anterior / Dovezi

Dacă trebuie să calculăm probabilitatea ca există incendiu dat fiind că există fum, atunci se va folosi următoarea ecuație:

P(Foc|Fum) = P(Fum|Foc) * P(Foc) / P(Fum)

Unde, P(Foc) este Priorul, P(Fum|Foc) este Probabilitatea și P(Fum) este dovada.

O ilustrare a teoremei lui Bayes

Este descris un exemplu de teoremă Bayes pentru a ilustra utilizarea teoremei Bayes într-o problemă.

Problemă

Sunt prezente trei casete etichetate ca A, B și C. Detaliile cutiilor sunt:

• Cutia A conține 2 bile roșii și 3 negre
• Cutia B conține 3 bile roșii și 1 neagră
• Și caseta C conține 1 bile roșie și 4 bile negre

Toate cele trei cutii sunt identice, având o probabilitate egală de a fi ridicate. Prin urmare, care este probabilitatea ca mingea roșie să fi fost ridicată din caseta A?

Soluţie

Fie că E indică evenimentul în care o minge roșie este ridicată și A, B și C indică faptul că mingea este ridicată din cutiile respective. Prin urmare, probabilitatea condiționată ar fi P(A|E) care trebuie calculată.

Probabilitățile existente P(A) = P(B) = P (C) = 1 / 3, deoarece toate casetele au probabilitatea egală de a fi alese.

P(E|A) = Numărul de bile roșii din caseta A / Numărul total de bile din caseta A = 2 / 5

În mod similar, P(E|B) = 3 / 4 și P(E|C) = 1 / 5

Atunci dovezile P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Prin urmare, P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Exemplu de teorema Bayes

Teorema Bayes dă probabilitatea unui „eveniment” cu informațiile date despre „teste”.

• Există o diferență între „evenimente” și „teste”. De exemplu, există un test pentru boala de ficat, care este diferit de a avea de fapt boala de ficat, adică un eveniment.
• Evenimentele rare ar putea avea o rată mai mare de fals pozitive.

Exemplul 1

Care este probabilitatea ca un pacient să aibă boală hepatică dacă este alcoolic?

Aici, „a fi alcoolic” este „testul” (tip de test de turnesol) pentru boala hepatică.

• A este evenimentul, adică „pacientul are boală hepatică””.

Conform înregistrărilor anterioare ale clinicii, se menționează că 10% dintre pacienții care intră în clinică suferă de boală hepatică.

Prin urmare, P(A)=0,10

• B este testul de turnesol că „Pacientul este alcoolic”.

Înregistrările anterioare ale clinicii au arătat că 5% dintre pacienții care intră în clinică sunt alcoolici.

Prin urmare, P(B)=0,05

• De asemenea, 7% dintre pacienții diagnosticați cu boală hepatică sunt alcoolici. Aceasta definește B|A: probabilitatea ca un pacient să fie alcoolic, având în vedere că are o boală hepatică este de 7%.

Conform formulei teoremei Bayes ,

P(A|B) = (0,07 * 0,1)/0,05 = 0,14

Prin urmare, pentru un pacient alcoolic, șansele de a avea o boală hepatică sunt de 0,14 (14%).

Exemplul2

• Incendiile periculoase sunt rare (1%)
• Dar fumul este destul de comun (10%) din cauza grătarelor,
• Și 90% dintre incendiile periculoase fac fum

Care este probabilitatea unui incendiu periculos atunci când există fum?

Calcul

P(Foc|Fum) =P(Foc) P(Fum|Foc)/P(Fum)

= 1% x 90%/10%

= 9%

Exemplul 3

Care sunt șansele de ploaie în timpul zilei? Unde, Rain înseamnă ploaie în timpul zilei, iar Cloud înseamnă dimineața înnorată.

Șansa de ploaie dată de Nor se scrie P(Ploaie|Nor)

P(Ploaie|Nor) = P(Ploaie) P(Nor|Ploaie)/P(Nor)

P(Ploaie) este probabilitatea ploii = 10%

P(Nor|Ploaie) este probabilitatea de apariție a norilor, având în vedere că se întâmplă ploaia = 50%

P(Cloud) este probabilitatea de apariție a norului = 40%

P(Ploaie|Nor) = 0,1 x 0,5/0,4 = .125

Prin urmare, o șansă de ploaie de 12,5%.

Aplicații

Există mai multe aplicații ale teoremei Bayes în lumea reală. Câteva aplicații principale ale teoremei sunt:

1. Modelarea ipotezelor

Teorema Bayes găsește o aplicație largă în învățarea automată aplicată și stabilește o relație între date și model. Învățarea automată aplicată utilizează procesul de testare și analiză a diferitelor ipoteze pe un anumit set de date.

Pentru a descrie relația dintre date și model, teorema Bayes oferă un model probabilistic.

P(h|D) = P(D|h) * P(h) / P(D)

Unde,

P(h|D): Probabilitatea posterioară a ipotezei

P(h): Probabilitatea anterioară a ipotezei.

O creștere a P(D) scade P(h|D). În schimb, dacă P(h) și probabilitatea de a observa datele date ipotezei crește, atunci probabilitatea P(h|D) crește.

2. Teorema Bayes pentru Clasificare

Metoda de clasificare presupune etichetarea unei date date. Acesta poate fi definit ca calculul probabilității condiționate a unei etichete de clasă dată unui eșantion de date.

P(clasa|date) = (P(date|clasa) * P(clasa)) / P(date)

Unde P(clasa|date) este probabilitatea clasei date fiind datele furnizate.

Calculul poate fi efectuat pentru fiecare clasă. Clasa cu cea mai mare probabilitate poate fi atribuită datelor de intrare.

Calculul probabilității condiționate nu este fezabil în condițiile unui număr mic de exemple. Prin urmare, aplicarea directă a teoremei Bayes nu este fezabilă. O soluție a modelului de clasificare constă în calculul simplificat.

• Clasificator Bayes naiv

Teorema Bayes consideră că variabilele de intrare sunt dependente de alte variabile care cauzează complexitatea calculului. Prin urmare, ipoteza este eliminată și fiecare variabilă de intrare este considerată ca o variabilă independentă. Ca rezultat, modelul se schimbă de la model de probabilitate condiționată dependentă la model de probabilitate condiționată independent. În cele din urmă, reduce complexitatea.

Această simplificare a teoremei Bayes este denumită Bayes naiv. Este utilizat pe scară largă pentru modele de clasificare și predicție.

• Clasificator optim Bayes

Acesta este un tip de model probabilistic care implică predicția unui nou exemplu dat de setul de date de antrenament. Un exemplu de clasificator optim Bayes este „Care este cea mai probabilă clasificare a noii instanțe, având în vedere datele de antrenament?”

Calculul probabilității condiționate a unei noi instanțe având în vedere datele de antrenament se poate face prin următoarea ecuație

P(vj | D) = suma {h în H} P(vj | hi) * P(hi | D)

Unde vj este o instanță nouă de clasificat,

H este setul de ipoteze pentru clasificarea instanței,

salut este o ipoteză dată,

P(vj | hi) este probabilitatea posterioară pentru vi dată de ipoteza hi, și

P(hi | D) este probabilitatea posterioară a ipotezei hi având în vedere datele D.

3. Utilizări ale teoremei Bayes în învățarea automată

Cea mai comună aplicație a teoremei Bayes în învățarea automată este dezvoltarea problemelor de clasificare. Alte aplicații, mai degrabă decât clasificarea, includ optimizarea și modelele casual.

• Optimizare bayesiana

Este întotdeauna o sarcină contestabilă să găsiți o intrare care are ca rezultat costul minim sau maxim al unei anumite funcții obiective. Optimizarea bayesiană se bazează pe teorema Bayes și oferă un aspect pentru căutarea unei probleme de optimizare globală. Metoda include construirea unui model probabilistic (funcția surogat), căutarea printr-o funcție de achiziție și selectarea eșantioanelor candidate pentru evaluarea funcției obiective reale.

În învățarea automată aplicată, optimizarea bayesiană este utilizată pentru a regla hiperparametrii unui model performant.

• Rețele de credință bayesiană

Relațiile dintre variabile pot fi definite prin utilizarea modelelor probabilistice. Ele sunt folosite și pentru calcularea probabilităților. Este posibil ca un model de probabilitate complet condiționat să nu poată calcula probabilitățile din cauza volumului mare de date. Naive Bayes a simplificat abordarea calculului. Totuși, există o altă metodă în care un model este dezvoltat pe baza dependenței condiționate cunoscute între variabile aleatoare și a independenței condiționate în alte cazuri. Rețeaua Bayesiană afișează această dependență și independență prin modelul grafic probabilistic cu muchii direcționate. Dependența condiționată cunoscută este afișată ca muchii direcționate, iar conexiunile lipsă reprezintă independențele condiționate din model.

4. Filtrarea Bayesiană a Spamului

Filtrarea spamului este o altă aplicație a teoremei Bayes. Două evenimente sunt prezente:

• Evenimentul A: Mesajul este spam.
• Testul X: mesajul conține anumite cuvinte (X)

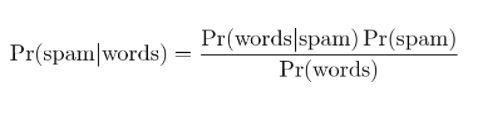
Prin aplicarea teoremei Bayes, se poate prezice dacă mesajul este spam, având în vedere „rezultatele testului”. Analizarea cuvintelor dintr-un mesaj poate calcula șansele de a fi un mesaj spam. Odată cu antrenarea filtrelor cu mesaje repetate, actualizează faptul că probabilitatea de a avea anumite cuvinte în mesaj ar fi spam.

O aplicație a teoremei Bayes cu un exemplu

Un producător de catalizator produce un dispozitiv pentru testarea defectelor unui anumit electrocatalizator (EC). Producătorul de catalizator susține că testul este fiabil în proporție de 97% dacă EC este defect și fiabil în proporție de 99% când este impecabil. Cu toate acestea, se poate aștepta ca 4% din EC menționate să fie defecte la livrare. Regula Bayes este aplicată pentru a stabili adevărata fiabilitate a dispozitivului. Seturile de evenimente de bază sunt

A: EC-ul este defect; A': CE este impecabil; B: EC este testat ca fiind defect; B': EC este testat pentru a fi impecabil.

Probabilitățile ar fi

B/A: EC este (cunoscut a fi) defect și testat defect, P(B/A) = 0,97,

B'/A: EC este (cunoscut ca fiind) defect, dar testat impecabil, P(B'/A)=1-P(B/A)=0,03,

B/A': EC este (cunoscut a fi) defect, dar testat defect, P(B/A') = 1- P(B'/A')=0,01

B'/A: = EC este (cunoscut a fi) impecabil și testat fără cusur P(B'/A') = 0,99

Probabilitățile calculate prin teorema Bayes sunt:

Probabilitatea de calcul arată că există o mare posibilitate de a respinge EC-uri impecabile (aproximativ 20%) și o posibilitate scăzută de a identifica EC-uri defecte (aproximativ 80%).

Concluzie

Una dintre caracteristicile cele mai izbitoare ale unei teoreme Bayes este că din câteva rapoarte de probabilitate se poate obține o cantitate imensă de informații. Cu mijloacele de probabilitate, probabilitatea unui eveniment anterior poate fi transformată în probabilitatea posterioară. Abordările teoremei Bayes pot fi aplicate în domeniile statisticii, epistemologiei și logicii inductive.

Dacă sunteți interesat să aflați mai multe despre Teorema Bayes, AI și învățarea automată, consultați Programul Executive PG de la IIIT-B și upGrad în Machine Learning și AI, care este conceput pentru profesioniști care lucrează și oferă peste 450 de ore de pregătire riguroasă, peste 30 de cazuri studii și sarcini, statutul de absolvenți IIIT-B, peste 5 proiecte practice practice și asistență la locul de muncă cu firme de top.