O que é o pensamento bayesiano? Introdução e Teorema

Um teorema estatístico dado pelo estatístico e filósofo inglês Thomas Bayes em 1700 continua a ser uma luz orientadora para cientistas e analistas em todo o mundo. Hoje, o pensamento bayesiano encontra aplicação na medicina, ciência, tecnologia e várias outras disciplinas e continua a influenciar fortemente nossa visão de mundo e ações resultantes.

A ideia de Thomas Bayes era surpreendentemente simples. De acordo com Bayes, a probabilidade de uma hipótese ser verdadeira depende de duas condições: quão razoável ela é baseada no que já sabemos (o conhecimento prévio) e quão bem ela se ajusta a novas evidências. Assim, o pensamento bayesiano difere do teste de hipóteses tradicional, pois o primeiro inclui o conhecimento prévio antes de tirar conclusões precipitadas.

Com a introdução preliminar em mente, vamos mergulhar um pouco mais em detalhes sobre as estatísticas Bayesianas.

Estatísticas Bayesianas

Em termos simples, a estatística Bayesiana aplica probabilidades a problemas estatísticos para atualizar crenças anteriores à luz da evidência de novos dados. A probabilidade expressa um grau de crença em um evento específico.

O grau de crença pode ser baseado em conhecimento prévio sobre o evento com base em suposições pessoais ou resultados de experimentos anteriores. Estatísticas Bayesianas usam o Teorema de Bayes para calcular probabilidades. O Teorema de Bayes, por sua vez, descreve a probabilidade condicional de um evento com base em novas evidências e informações prévias relacionadas ao evento.

Com isso em mente, vamos retocar o conceito fundamental de probabilidade condicional antes de entendermos o Teorema de Bayes em profundidade.

Probabilidade Condicional

A probabilidade condicional pode ser definida como a probabilidade de um evento ou resultado com base na ocorrência de um evento ou resultado anterior. É calculado multiplicando a probabilidade do evento anterior pela probabilidade do evento subsequente ou condicional.

Vamos dar uma olhada em um exemplo para entender melhor o conceito .

• O evento A é que uma família planejando um passeio vai fazer um piquenique. Há 80% de chance de que a família vá ao piquenique.
• O evento B é que vai chover no dia em que a família sair para um piquenique. A previsão do tempo diz que há 60% de chance de chuva no dia do piquenique.
• Assim, a probabilidade (P) de que a família vá ao piquenique e chova é calculada da seguinte forma:

P (Piquenique e chuva) = P (Chuva | Piquenique) P (Piquenique) = (0,60) * (0,80) = 0,48

No exemplo acima, a probabilidade condicional analisa os dois eventos A e B em relação um com o outro, ou seja, a probabilidade de que a família vá ao piquenique e também chova no mesmo dia.

Portanto, a probabilidade condicional difere da probabilidade incondicional porque a última se refere à probabilidade de ocorrência de um evento, independentemente de qualquer outro evento ou eventos terem ocorrido ou quaisquer outras condições estarem presentes.

A fórmula da probabilidade condicional

A fórmula para probabilidade condicional vem da regra de multiplicação de probabilidade:

P (A e B) ou P (AUB) = P (B dado A) ou P (B | A) * P (A)

Na equação acima, P (A e B) é a probabilidade conjunta, referindo-se à probabilidade de dois ou mais eventos ocorrerem simultaneamente. Também é escrito como P(A,B).

Veja como deduzir a equação de probabilidade condicional da regra de multiplicação:

Passo 1: Escreva a regra da multiplicação.

P (A e B) = P (B | A) * P (A)

Passo 2: Divida ambos os lados da equação por P (A).

P (A e B) / P (A) = P (B | A) * P (A) / P (A)

Passo 3: Cancele P (A) no lado direito da equação.

P (A e B) / P (A) = P (B | A)

Passo 4: Reescreva a equação.

P (A e B) = P (B | A) / P (A)

Assim, a fórmula para probabilidade condicional é dada como:

P (A e B) = P (B | A) / P (A)

Teorema de Bayes

Usando o Teorema de Bayes, podemos atualizar nossas crenças e convicções com base em novas e relevantes evidências. Por exemplo, se estamos tentando descobrir a probabilidade de uma determinada pessoa ter câncer, geralmente assumimos que é a porcentagem da população que tem câncer. No entanto, se introduzirmos evidências extras, como a pessoa em questão é um fumante regular, podemos atualizar nossa percepção (e, portanto, a probabilidade), pois a probabilidade de ter câncer é maior se o indivíduo for fumante. Portanto, utilizamos nosso conhecimento prévio e as evidências adicionais para melhorar nossas estimativas.

A fórmula do Teorema de Bayes

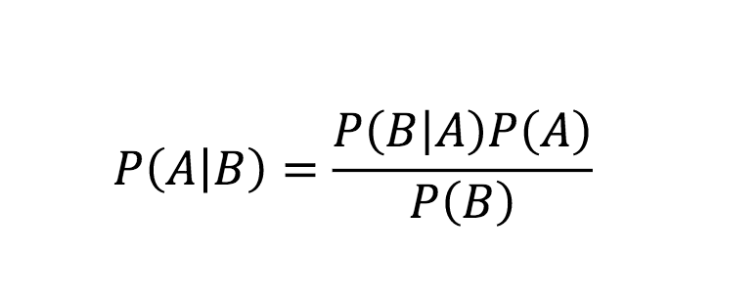
Fonte

A equação acima é a regra de Bayes. Agora, vamos olhar para a derivação passo a passo da equação do Teorema de Bayes.

Passo 1: Considere dois eventos, A e B. A é o evento cuja probabilidade queremos calcular e B é a evidência adicional relacionada a A.

Passo 2: Escreva a relação entre a probabilidade conjunta e a probabilidade condicional dos eventos A e B.

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

Etapa 3: Defina os dois termos de probabilidade condicional iguais entre si.

P (A | B) * P(B) = P (B | A) * P(A)

Passo 4: Divida ambos os lados da equação por P (B).

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

Passo 5: Cancele P (B) no lado esquerdo da equação.

P (A | B) = P (B | A) * P(A) / P (B)

Assim, obtemos a fórmula do Teorema de Bayes da seguinte forma:

P (A | B) = P (B | A) * P(A) / P (B)

Entendendo os termos da equação do Teorema de Bayes

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B) é chamado de probabilidade posterior ou a probabilidade que estamos tentando estimar. Com base no exemplo anterior, a probabilidade posterior seria a probabilidade de a pessoa ter câncer, dado que a pessoa é fumante regular.
• P (B | A) é chamado de probabilidade , referindo-se à probabilidade de detectar a evidência adicional, dada nossa hipótese inicial. No exemplo acima, a probabilidade é a probabilidade de a pessoa ser fumante, dado que a pessoa tem câncer.
• P (A) é a probabilidade anterior ou a probabilidade de nossa hipótese sem qualquer evidência ou informação adicional. No exemplo acima, a probabilidade anterior é a probabilidade de ter câncer.
• P (B) é a probabilidade marginal ou a probabilidade total de observar a evidência. No contexto do exemplo acima, a probabilidade marginal é a probabilidade de ser fumante.

Um exemplo simples para entender o teorema de Bayes

Usando alguns números hipotéticos no exemplo anterior, veremos o efeito da aplicação do Teorema de Bayes.

Suponha que a probabilidade de ter câncer seja 0,06, ou seja, 6% das pessoas têm câncer. Agora, digamos que a probabilidade de ser fumante é de 0,20 ou 20% das pessoas são fumantes e 30% das pessoas com câncer são fumantes. Então, P (Fumante | Câncer) = 0,30.

Inicialmente, a probabilidade de ter câncer é simplesmente 0,06 (anterior). Mas, usando as novas evidências, podemos calcular P (Câncer | Fumante) = P ((Fumante | Câncer) * P (Câncer)) / P (Fumante) = (0,30*0,06) / (0,20) = 0,09.

Aprenda cursos de ciência de dados online das melhores universidades do mundo. Ganhe Programas PG Executivos, Programas de Certificado Avançado ou Programas de Mestrado para acelerar sua carreira.

Caminho a seguir: domine os conceitos de estatística para uma carreira em ciência de dados ou aprendizado de máquina

A plataforma de ensino superior EdTech da upGrad impactou mais de 500.000 profissionais que trabalham em todo o mundo com sua infinidade de cursos e experiências de aprendizado imersivas. Com uma base de mais de 40.000 alunos espalhados por mais de 85 países, os cursos relevantes para o setor do upGrad garantem o avanço de sua carreira em seu campo de escolha.

O Mestrado em Ciência de Dados é um curso de 18 meses que transmite as principais habilidades em Estatística, Análise Preditiva, Aprendizado de Máquina, Análise de Big Data, Visualização de Dados, etc.

Destaques do programa:

• Mestrado pela Liverpool John Moores University e Executive PGP pelo IIIT Bangalore
• Mais de 500 horas de conteúdo, mais de 60 estudos de caso e projetos, mais de 20 sessões ao vivo, mais de 14 linguagens e ferramentas de programação
• Rede do setor, sessões de resolução de dúvidas e suporte ao aprendizado

O Advanced Certificate Program in Machine Learning and Deep Learning é um curso rigoroso de 6 meses com oportunidades de networking entre pares, projetos práticos, orientação do setor e assistência profissional de 360 ​​graus.

Destaques do programa:

• Reconhecimento de prestígio do IIIT Bangalore
• Mais de 240 horas de conteúdo, mais de 5 estudos de caso e projetos, mais de 24 sessões ao vivo, cobertura de 12 linguagens de programação, ferramentas e bibliotecas
• Sessões de coaching em grupo 1:8 e sessões de mentoria 1:1 com especialistas do setor

Conclusão

O pensamento bayesiano sustenta várias áreas do pensamento humano, investigação e crença, embora a maioria de nós não tenha consciência disso. Do rastreamento do câncer e do aquecimento global à política monetária e avaliação de risco e seguro , o pensamento bayesiano é fundamental. Acredita-se que até o famoso matemático britânico Alan Turing empregou a abordagem Bayesiana para decifrar o Código Enigma Alemão durante a Segunda Guerra Mundial.

Inscreva-se no upGrad e aprofunde seu conhecimento dos principais conceitos estatísticos e muito mais!