Regressão polinomial: importância, implementação passo a passo

Introdução

Nesse vasto campo de Machine Learning, qual seria o primeiro algoritmo que a maioria de nós teria estudado? Sim, é a Regressão Linear. Principalmente sendo o primeiro programa e algoritmo que alguém teria aprendido em seus primeiros dias de programação de aprendizado de máquina, a regressão linear tem sua própria importância e poder com um tipo linear de dados.

E se o conjunto de dados que encontramos não for linearmente separável? E se o modelo de regressão linear não for capaz de derivar nenhum tipo de relação entre as variáveis ​​independentes e dependentes?

Aí vem outro tipo de regressão conhecido como Regressão Polinomial. Fiel ao seu nome, Regressão Polinomial é um algoritmo de regressão que modela a relação entre a variável dependente (y) e a variável independente (x) como um polinômio de grau n. Neste artigo, vamos entender o algoritmo e a matemática por trás da regressão polinomial, juntamente com sua implementação em Python.

O que é regressão polinomial?

Conforme definido anteriormente, a Regressão Polinomial é um caso especial de regressão linear em que uma equação polinomial com um grau (n) especificado é ajustada nos dados não lineares que formam uma relação curvilínea entre as variáveis ​​dependentes e independentes.

y= b 0 +b 1 x 1 + b 2 x 1 2 + b 3 x 1 3 +…… b n x 1 n

Aqui,

y é a variável dependente (variável de saída)

x1 é a variável independente (preditores)

b 0 é o viés

b 1 , b 2 , ….b n são os pesos na equação de regressão.

À medida que o grau da equação polinomial ( n ) aumenta, a equação polinomial torna-se mais complicada e existe a possibilidade do modelo tender a overfit, o que será discutido na parte posterior.

Comparação de Equações de Regressão

Regressão Linear Simples ===> y= b0+b1x

Regressão Linear Múltipla ===> y= b0+b1x1+ b2x2+ b3x3+…… bnxn

Regressão Polinomial ===> y= b0+b1x1+ b2x12+ b3x13+…… bnx1n

Das três equações acima, vemos que existem várias diferenças sutis nelas. As Regressões Lineares Simples e Múltiplas são diferentes da equação de Regressão Polinomial, pois tem um grau de apenas 1. A Regressão Linear Múltipla consiste em várias variáveis ​​x1, x2, e assim por diante. Embora a equação de regressão polinomial tenha apenas uma variável x1, ela tem um grau n que a diferencia das outras duas.

Necessidade de regressão polinomial

A partir dos diagramas abaixo, podemos ver que no primeiro diagrama, tenta-se ajustar uma linha linear no conjunto dado de pontos de dados não lineares. Entende-se que fica muito difícil para uma linha reta formar uma relação com esses dados não lineares. Por isso, quando treinamos o modelo, a função de perda aumenta causando o alto erro.

Por outro lado, quando aplicamos a Regressão Polinomial é claramente visível que a linha se encaixa bem nos pontos de dados. Isso significa que a equação polinomial que se ajusta aos pontos de dados deriva algum tipo de relação entre as variáveis ​​no conjunto de dados. Assim, para os casos em que os pontos de dados estão dispostos de forma não linear, necessitamos do modelo de Regressão Polinomial.

Implementação de regressão polinomial em Python

A partir daqui, construiremos um modelo de Machine Learning em Python implementando a Regressão Polinomial. Compararemos os resultados obtidos com Regressão Linear e Regressão Polinomial. Vamos primeiro entender o problema que vamos resolver com a regressão polinomial.

Descrição do Problema

Neste caso, considere o caso de uma Start-up que pretende contratar vários candidatos de uma empresa. Existem diferentes vagas para diferentes cargos na empresa. A start-up tem detalhes do salário para cada função na empresa anterior. Assim, quando um candidato menciona seu salário anterior, o RH da start-up precisa verificá-lo com os dados existentes. Assim, temos duas variáveis ​​independentes que são Posição e Nível. A variável dependente (saída) é o Salário que deve ser previsto usando a Regressão Polinomial.

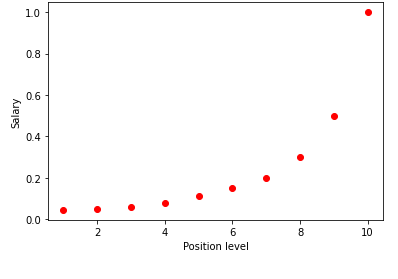
Ao visualizar a tabela acima em um gráfico, vemos que os dados são de natureza não linear. Em outras palavras, à medida que o nível aumenta, o salário aumenta a uma taxa mais alta, dando-nos uma curva conforme mostrado abaixo.

Etapa 1: pré-processamento de dadosA primeira etapa na construção de qualquer modelo de Machine Learning é importar as bibliotecas. Aqui, temos apenas três bibliotecas básicas a serem importadas. Depois disso, o conjunto de dados é importado do meu repositório GitHub e as variáveis ​​dependentes e independentes são atribuídas. As variáveis ​​independentes são armazenadas na variável X e a variável dependente é armazenada na variável y.

importar numpy como np

importar matplotlib.pyplot como plt

importar pandas como pd

conjunto de dados = pd.read_csv('https://raw.githubusercontent.com/mk-gurucharan/Regression/master/PositionSalaries_Data.csv')

X = dataset.iloc[:, 1:-1].values

y = dataset.iloc[:, -1].values

Aqui no termo [:, 1:-1], os primeiros dois pontos representam que todas as linhas devem ser tomadas e o termo 1:-1 denota que as colunas a serem incluídas são da primeira coluna até a penúltima coluna que é dada por -1.

Etapa 2: modelo de regressão linearNa próxima etapa, construiremos um modelo de Regressão Linear Múltipla e o utilizaremos para prever os dados salariais das variáveis ​​independentes. Para isso, a classe LinearRegression é importada da biblioteca sklearn. Em seguida, é ajustado nas variáveis ​​X e y para fins de treinamento.

de sklearn.linear_model importar LinearRegression

regressor = LinearRegression()

regressor.fit(X, y)

Uma vez construído o modelo, ao visualizar os resultados, obtemos o gráfico a seguir.

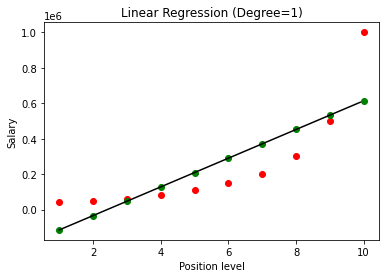
Como se vê claramente, ao tentar ajustar uma linha reta em um conjunto de dados não linear, não há relação derivada pelo modelo de Machine Learning. Assim, precisamos ir para a Regressão Polinomial para obter uma relação entre as variáveis.

Etapa 3: Modelo de regressão polinomialNeste próximo passo, vamos ajustar um modelo de Regressão Polinomial neste conjunto de dados e visualizar os resultados. Para isso, importamos outra classe do módulo sklearn denominada PolynomialFeatures na qual damos o grau da equação polinomial a ser construída. Em seguida, a classe LinearRegression é usada para ajustar a equação polinomial ao conjunto de dados.

de sklearn.preprocessing import PolynomialFeatures

de sklearn.linear_model importar LinearRegression

poly_reg = PolynomialFeatures(grau = 2)

X_poly = poly_reg.fit_transform(X)

lin_reg = LinearRegression()

lin_reg.fit(X_poly, y)

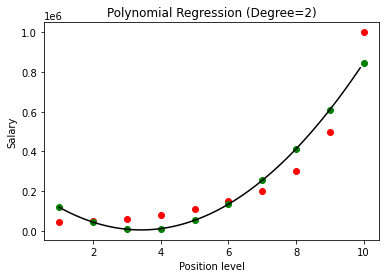
No caso acima, demos o grau da equação polinomial para ser igual a 2. Ao traçar o gráfico, vemos que existe algum tipo de curva que é derivada, mas ainda há muito desvio dos dados reais (em vermelho ) e os pontos de curva previstos (em verde). Assim, na próxima etapa, aumentaremos o grau do polinômio para números mais altos, como 3 e 4, e depois compararemos entre si.

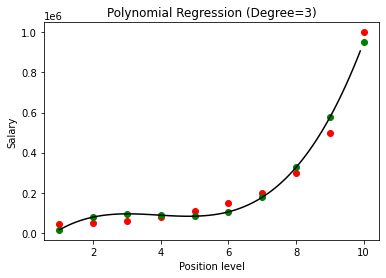
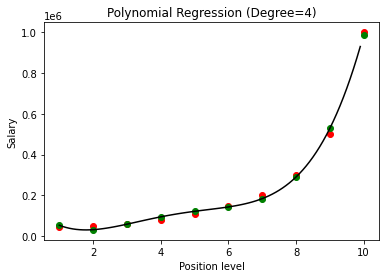
Ao comparar os resultados da Regressão Polinomial com os graus 3 e 4, vemos que à medida que o grau aumenta, o modelo treina bem com os dados. Assim, podemos inferir que um grau mais alto permite que a equação polinomial se ajuste com mais precisão aos dados de treinamento. No entanto, este é o caso perfeito de overfitting. Assim, torna-se importante escolher o valor de n precisamente para evitar o overfitting.

O que é Overfitting?

Como o nome diz, o Overfitting é denominado como uma situação em estatística quando uma função (ou um modelo de Machine Learning, neste caso) se ajusta muito a um conjunto de pontos de dados limitados. Isso faz com que a função tenha um desempenho ruim com novos pontos de dados.

Em Aprendizado de Máquina, se um modelo é considerado overfitting em um determinado conjunto de pontos de dados de treinamento, quando o mesmo modelo é introduzido em um conjunto completamente novo de pontos (digamos, o conjunto de dados de teste), ele tem um desempenho muito ruim como o modelo de overfitting não generalizou bem com os dados e está apenas overfitting nos pontos de dados de treinamento.

Na regressão polinomial, há uma boa chance de o modelo ficar overfit nos dados de treinamento à medida que o grau do polinômio é aumentado. No exemplo mostrado acima, vemos um caso típico de overfitting na regressão polinomial que pode ser corrigido apenas com uma base de tentativa e erro para escolher o valor ideal do grau.

Leia também: Ideias de projetos de aprendizado de máquina

Conclusão

Para concluir, a Regressão Polinomial é utilizada em muitas situações onde há uma relação não linear entre as variáveis ​​dependentes e independentes. Embora esse algoritmo sofra de sensibilidade em relação a valores discrepantes, ele pode ser corrigido tratando-os antes de ajustar a linha de regressão. Assim, neste artigo, fomos apresentados ao conceito de Regressão Polinomial juntamente com um exemplo de sua implementação em Programação Python em um conjunto de dados simples.

Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o PG Diploma in Machine Learning & AI do IIIT-B e upGrad, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT- B Status de ex-aluno, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.

Aprenda ML Course das melhores universidades do mundo. Ganhe Masters, Executive PGP ou Advanced Certificate Programs para acelerar sua carreira.

O que você entende por regressão linear?

A regressão linear é um tipo de análise numérica preditiva através da qual podemos encontrar o valor de uma variável desconhecida com a ajuda de uma variável dependente. Também explica a conexão entre uma variável dependente e uma ou mais variáveis ​​independentes. A regressão linear é uma técnica estatística para demonstrar uma ligação entre duas variáveis. A regressão linear traça uma linha de tendência de um conjunto de pontos de dados. A regressão linear pode ser usada para gerar um modelo de previsão a partir de dados aparentemente aleatórios, como diagnósticos de câncer ou preços de ações. Existem vários métodos para calcular a regressão linear. A abordagem comum dos mínimos quadrados, que estima variáveis ​​desconhecidas nos dados e transforma visualmente na soma das distâncias verticais entre os pontos de dados e a linha de tendência, é uma das mais prevalentes.

Quais são algumas das desvantagens da regressão linear?

Na maioria dos casos, a análise de regressão é usada em pesquisas para estabelecer que existe uma ligação entre as variáveis. No entanto, a correlação não implica causalidade, uma vez que uma ligação entre duas variáveis ​​não implica que uma faça com que a outra aconteça. Mesmo uma linha em uma regressão linear básica que se adapte bem aos pontos de dados pode não garantir uma relação entre as circunstâncias e os resultados lógicos. Usando um modelo de regressão linear, você pode determinar se existe ou não alguma correlação entre as variáveis. Investigação extra e análise estatística serão necessárias para determinar a natureza exata do link e se uma variável causa a outra.

Quais são os pressupostos básicos da regressão linear?

Na regressão linear, existem três suposições principais. As variáveis ​​dependentes e independentes devem, antes de tudo, ter uma conexão linear. Um gráfico de dispersão das variáveis ​​dependentes e independentes é usado para verificar essa relação. Em segundo lugar, deve haver multicolinearidade mínima ou nula entre as variáveis ​​independentes no conjunto de dados. Isso implica que as variáveis ​​independentes não estão relacionadas. O valor deve ser limitado, o que é determinado pelo requisito de domínio. A homocedasticidade é o terceiro fator. A suposição de que os erros são distribuídos uniformemente é uma das suposições mais essenciais.