Aprenda o algoritmo Naive Bayes para aprendizado de máquina [com exemplos]
Publicados: 2021-02-25Índice
Introdução
Em matemática e programação, algumas das soluções mais simples são geralmente as mais poderosas. O Algoritmo Bayes ingênuo vem como um exemplo clássico dessa afirmação. Mesmo com o forte e rápido avanço e desenvolvimento no campo do Machine Learning, este Algoritmo Naive Bayes ainda se mantém forte como um dos algoritmos mais utilizados e eficientes. O Naive Bayes Algorithm encontra suas aplicações em uma variedade de problemas, incluindo tarefas de classificação e problemas de processamento de linguagem natural (NLP).
A hipótese matemática do Teorema de Bayes serve como o conceito fundamental por trás deste Algoritmo Naive Bayes. Neste artigo, abordaremos o básico do Teorema de Bayes, o Algoritmo Naive Bayes e sua implementação em Python com um problema de exemplo em tempo real. Junto com estes, também veremos algumas vantagens e desvantagens do Algoritmo Naive Bayes em comparação com seus concorrentes.
Noções básicas de probabilidade
Antes de nos aventurarmos a entender o Teorema de Bayes e o Algoritmo Naive Bayes, vamos aprimorar nosso conhecimento existente sobre os fundamentos da Probabilidade.
Como todos sabemos por definição, dado um evento A, a probabilidade desse evento ocorrer é dada por P(A). Em probabilidade, dois eventos A e B são denominados eventos independentes se a ocorrência do evento A não altera a probabilidade de ocorrência do evento B e vice-versa. Por outro lado, se a ocorrência de um altera a probabilidade do outro, então eles são chamados de eventos dependentes.
Vamos ser apresentados a um novo termo chamado Probabilidade Condicional . Em matemática, a Probabilidade Condicional para dois eventos A e B dados por P (A| B) é definida como a probabilidade de ocorrência do evento A dado que o evento B já ocorreu. Dependendo da relação entre os dois eventos A e B quanto a serem dependentes ou independentes, a Probabilidade Condicional é calculada de duas maneiras.
- A probabilidade condicional de dois eventos dependentes A e B é dada por P (A| B) = P (A e B) / P (B)
- A expressão para a probabilidade condicional de dois eventos independentes A e B é dada por, P (A| B) = P (A)
Conhecendo a matemática por trás das Probabilidades e das Probabilidades Condicionais, vamos agora para o Teorema de Bayes.

Teorema de Bayes
Em estatística e teoria da probabilidade, o Teorema de Bayes também conhecido como regra de Bayes é usado para determinar a probabilidade condicional de eventos. Em outras palavras, o teorema de Bayes descreve a probabilidade de um evento com base no conhecimento prévio das condições que podem ser relevantes para o evento.
Para entendê-lo de uma forma mais simples, considere que precisamos saber que a probabilidade do preço de uma casa ser muito alta. Se soubermos sobre os outros parâmetros, como a presença de escolas, lojas médicas e hospitais nas proximidades, podemos fazer uma avaliação mais precisa dos mesmos. Isso é exatamente o que o Teorema de Bayes realiza.
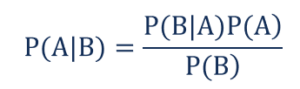
De tal modo que,
- P(A|B) – a probabilidade condicional do evento A ocorrer, dado que o evento B ocorreu também conhecido como Probabilidade Posterior .
- P(B|A) – a probabilidade condicional do evento B ocorrer, dado que o evento A ocorreu também conhecido como Probabilidade de Verossimilhança .
- P(A) – a probabilidade do evento A ocorrer também conhecido como Probabilidade Antecipada.
- P(B) – a probabilidade do evento B ocorrer também conhecido como Probabilidade Marginal.
Suponha que temos um problema simples de Machine Learning com 'n' variáveis independentes e a variável dependente que é a saída é um valor booleano (True ou False). Suponha que os atributos independentes sejam de natureza categórica, vamos considerar 2 categorias para este exemplo. Portanto, com esses dados, precisamos calcular o valor da Probabilidade de Verossimilhança, P(B|A).
Portanto, ao observar o acima, descobrimos que precisamos calcular 2*(2^ n -1 ) parâmetros para aprender esse modelo de Machine Learning. Da mesma forma, se tivermos 30 atributos independentes booleanos, o número total de parâmetros a serem calculados será próximo a 3 bilhões, o que é extremamente alto em custo computacional.
Essa dificuldade em construir um modelo de Machine Learning com o Teorema de Bayes levou ao nascimento e desenvolvimento do Algoritmo Naive Bayes.
Algoritmo Naive Bayes
Para ser prático, a complexidade do Teorema de Bayes acima mencionada precisa ser reduzida. Isso é exatamente alcançado no Algoritmo Naive Bayes fazendo poucas suposições. As suposições feitas são de que cada recurso faz uma contribuição independente e igual para o resultado.
O Naive Bayes Algorithm é um algoritmo de aprendizado supervisionado e é baseado no teorema de Bayes que é usado principalmente na resolução de problemas de classificação. É um dos classificadores mais simples e precisos que constroem modelos de Machine Learning para fazer previsões rápidas. Matematicamente, é um classificador probabilístico, pois faz previsões usando a função de probabilidade dos eventos.
Exemplo de problema
Para entender a lógica por trás das suposições, vamos passar por um conjunto de dados simples para obter uma melhor intuição.
| Cor | Tipo | Origem | Roubo? |
| Preto | Sedã | Importado | sim |
| Preto | SUV | Importado | Não |
| Preto | Sedã | Doméstico | sim |
| Preto | Sedã | Importado | Não |
| Castanho | SUV | Doméstico | sim |
| Castanho | SUV | Doméstico | Não |
| Castanho | Sedã | Importado | Não |
| Castanho | SUV | Importado | sim |
| Castanho | Sedã | Doméstico | Não |
A partir do conjunto de dados fornecido acima, podemos derivar os conceitos das duas suposições que definimos para o Algoritmo Naive Bayes acima.
- A primeira suposição é que todas as características são independentes umas das outras. Aqui, vemos que cada atributo é independente, como a cor “Vermelho” é independente do Tipo e Origem do carro.
- Em seguida, cada recurso deve receber igual importância. Da mesma forma, apenas ter conhecimento sobre o Tipo e Origem do Carro não é suficiente para prever a saída do problema. Portanto, nenhuma das variáveis é irrelevante e, portanto, todas elas contribuem igualmente para o resultado.
Para resumir, A e B são condicionalmente independentes dado C se e somente se, dado o conhecimento de que C ocorre, saber se A ocorre não fornece informações sobre a probabilidade de ocorrência de B, e saber se B ocorre não fornece informações sobre probabilidade de ocorrência de A. Essas suposições tornam o algoritmo de Bayes – Naive . Daí o nome, Algoritmo Naive Bayes.
Portanto, para o problema dado acima, o Teorema de Bayes pode ser reescrito como –
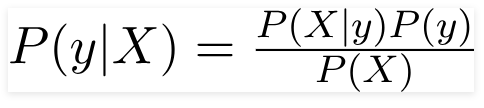
De tal modo que,
- O vetor de características independentes, X = (x 1 , x 2 , x 3 ……x n ) representando as características como Cor, Tipo e Origem do Carro.
- A variável de saída y tem apenas dois resultados Sim ou Não.
Assim, substituindo os valores acima, obtemos a Fórmula Naive Bayes como,
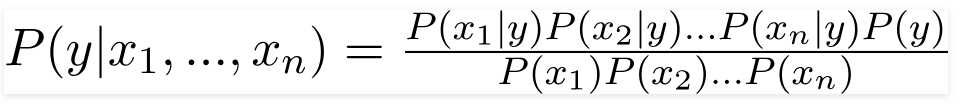
Para calcular a probabilidade posterior P(y|X), temos que criar uma Tabela de Frequências para cada atributo em relação à saída. Em seguida, convertendo as tabelas de frequência em tabelas de probabilidade, após o que finalmente usamos a equação Naive Bayesiana para calcular a probabilidade posterior para cada classe. A classe com a maior probabilidade posterior é escolhida como resultado da previsão. Abaixo estão as tabelas de frequência e probabilidade para todos os três preditores.
Tabela de frequência de cores Tabela de probabilidade de cores
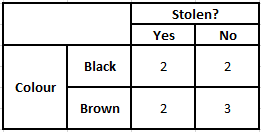
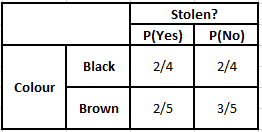
Tabela de Frequência do Tipo Tabela de Probabilidade do Tipo
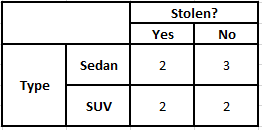
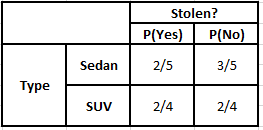

Tabela de Frequência de Origem Tabela de Probabilidade de Origem
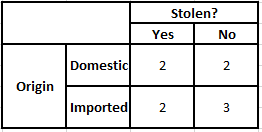
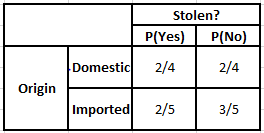
Considere o caso em que precisamos calcular as probabilidades posteriores para as condições dadas abaixo –
| Cor | Tipo | Origem |
| Castanho | SUV | Importado |
Assim, a partir da fórmula dada acima, podemos calcular as Probabilidades Posteriores como mostrado abaixo–
P(Sim | X) = P(Marrom | Sim) * P(SUV | Sim) * P(Importado | Sim) * P(Sim)
= 2/5 * 2/4 * 2/5 * 1
= 0,08
P(Não | X) = P(Marrom | Não) * P(SUV | Não) * P(Importado | Não) * P(Não)
= 3/5 * 2/4 * 3/5 * 1
= 0,18
A partir dos valores calculados acima, como as Probabilidades Posteriores para Não é Maior que Sim (0,18>0,08), pode-se inferir que um carro de Cor Marrom, Tipo SUV de Origem Importada é classificado como “Não”. Portanto, o carro não é roubado.
Implementação em Python
Agora que entendemos a matemática por trás do algoritmo Naive Bayes e também o visualizamos com um exemplo, vamos analisar seu código de Machine Learning na linguagem Python.
Relacionado: Classificador Naive Bayes
Analise de problemas
Para implementar o programa Naive Bayes Classification em Machine Learning usando Python, usaremos o famoso 'Iris Flower Dataset'. O conjunto de dados de flores de íris ou conjunto de dados de Fisher's Iris é um conjunto de dados multivariado introduzido pelo estatístico, eugenista e biólogo britânico Ronald Fisher em 1998. Este é um conjunto de dados muito pequeno e básico que consiste em muito menos dados numéricos contendo informações sobre 3 classes de flores pertencentes à espécie Iris que são –
- Íris Setosa
- Íris Versicolor
- Íris Virgínia
Existem 50 amostras de cada uma das três espécies , totalizando um conjunto de dados de 150 linhas. Os 4 atributos (ou) variáveis independentes que são usadas neste conjunto de dados são –
- comprimento da sépala em cm
- largura da sépala em cm
- comprimento da pétala em cm
- largura da pétala em cm
A variável dependente é a “ espécie ” da flor que é identificada pelos quatro atributos dados acima.
Passo 1 – Importando as Bibliotecas
Como sempre, a principal etapa na construção de qualquer modelo de Machine Learning será importar as bibliotecas relevantes. Para isso, carregaremos as bibliotecas NumPy, Mathplotlib e Pandas para pré-processamento dos dados.
importar numpy como np
importar matplotlib.pyplot como plt
importar pandas como pd
Passo 2 – Carregando o conjunto de dados
O conjunto de dados da flor Iris a ser usado para treinar o classificador Naive Bayes deve ser carregado em um Pandas DataFrame. As 4 variáveis independentes devem ser atribuídas à variável X e a variável da espécie de saída final é atribuída a y.
dataset = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = dataset.iloc[:,:4].values
y = dataset['species'].valuesdataset.head(5)>>
sepal_length sepal_width petal_length petal_width espécies
5,1 3,5 1,4 0,2 setosa
4,9 3,0 1,4 0,2 setosa
4,7 3,2 1,3 0,2 setosa
4,6 3,1 1,5 0,2 setosa
5,0 3,6 1,4 0,2 setosa
Passo 3 – Dividindo o conjunto de dados em conjunto de treinamento e conjunto de teste
Após carregar o conjunto de dados e as variáveis, o próximo passo é preparar as variáveis que serão submetidas ao processo de treinamento. Nesta etapa, temos que dividir as variáveis X e y para os conjuntos de dados de treinamento e teste. Para isso, devemos atribuir 80% dos dados aleatoriamente ao conjunto de treinamento que será usado para fins de treinamento e os 20% restantes dos dados como o conjunto de teste no qual o Classificador Naive Bayes treinado será testado quanto à precisão.
de sklearn.model_selection importar train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0,2)
Etapa 4 - Dimensionamento de recursos
Embora este seja um processo adicional para este pequeno conjunto de dados, estou adicionando isso para você usá-lo em um conjunto de dados maior. Neste, os dados nos conjuntos de treinamento e teste são reduzidos para um intervalo de valores entre 0 e 1. Isso reduz o custo computacional.
de sklearn.preprocessing importação StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
Etapa 5 – Treinar o modelo de Classificação Naive Bayes no Conjunto de Treinamento
É nesta etapa que importamos a classe Naive Bayes da biblioteca sklearn. Para este modelo, utilizamos o modelo Gaussiano, existem vários outros modelos como Bernoulli, Categórico e Multinomial. Assim, o X_train e o y_train são ajustados à variável do classificador para fins de treinamento.
de sklearn.naive_bayes importar GaussianNB
classificador = GaussianNB()
classificador.fit(X_train, y_train)
Passo 6 – Previsão dos resultados do conjunto de testes –
Prevemos a classe da espécie para o conjunto de teste usando o modelo treinado e comparamos com os valores reais da classe da espécie.
y_pred = classificador.predict(X_test)
df = pd.DataFrame({'Real Values':y_test, 'Predicted Values':y_pred})
df>>
Valores Reais Valores Previstos
setosa setosa
setosa setosa
virginica virginica
versicolor versicolor
setosa setosa
setosa setosa
… … … … …
virginica versicolor
virginica virginica
setosa setosa
setosa setosa
versicolor versicolor
versicolor versicolor
Na comparação acima, vemos que há uma previsão incorreta que previu Versicolor em vez de virginica.
Passo 7 – Matriz de Confusão e Precisão
Como estamos lidando com Classificação, a melhor maneira de avaliar nosso modelo classificador é imprimir a Matriz de Confusão junto com sua precisão no conjunto de teste.
de sklearn.metrics importar confusão_matrix
cm = confusão_matrix(y_test, y_pred)de sklearn.metrics import precision_score

print ("Precisão: ", precisão_score(y_test, y_pred))
cm>>Precisão: 0,9666666666666667
>>matriz([[14, 0, 0],
[0, 7, 0],
[0, 1, 8]])
Conclusão
Assim, neste artigo, passamos pelo básico do Algoritmo Naive Bayes, entendemos a matemática por trás da Classificação junto com um exemplo resolvido à mão. Por fim, implementamos um código de Machine Learning para resolver um conjunto de dados popular usando o algoritmo Naive Bayes Classification.
Se você estiver interessado em aprender mais sobre IA, aprendizado de máquina, confira o Diploma PG do IIIT-B e do upGrad em aprendizado de máquina e IA, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, Status de ex-aluno do IIIT-B, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.
Como a probabilidade é útil no aprendizado de máquina?
Podemos ter que tomar decisões com base em informações parciais ou incompletas em cenários do mundo real. A probabilidade nos ajuda a quantificar as incertezas em tais sistemas e gerenciar o risco da tarefa. O método tradicional funciona apenas para os resultados determinísticos de ações específicas, mas sempre há algum escopo de incerteza em qualquer modelo de previsão. Essa incerteza pode vir de muitos parâmetros dos dados de entrada, como Ruído nos dados. Além disso, visões bayesianas de teoremas de probabilidade podem ajudar no reconhecimento de padrões a partir dos dados de entrada. Para isso, a probabilidade usa o conceito de estimativa de máxima verossimilhança e, portanto, é útil para produzir resultados relevantes.
Para que serve a Matriz de Confusão?
A matriz de confusão é uma matriz 2x2 usada para interpretar o desempenho do modelo de classificação. Os valores verdadeiros para os dados de entrada devem ser conhecidos para que isso funcione, portanto, não podem ser representados para dados não rotulados. Consiste no número de falsos positivos (FP), verdadeiros positivos (TP), falsos negativos (FN) e verdadeiros negativos (TN). As previsões são classificadas nessas classes usando a contagem do conjunto de treinamento e do conjunto de teste. Ele nos ajuda a visualizar parâmetros úteis, como exatidão, precisão, recall e especificidade. É relativamente fácil de entender e dá uma ideia clara sobre o algoritmo.
Quais são os diferentes tipos de modelo Naive Bayes?
Todos os tipos são baseados principalmente no Teorema de Bayes. O modelo Naive Bayes geralmente tem três tipos: Gaussiano, Bernoulli e Multinomial. O Gaussian Naive Bayes auxilia com valores contínuos dos parâmetros de entrada, e assume que todas as classes de dados de entrada são distribuídas uniformemente. O Naive Bayes de Bernoulli é um modelo baseado em eventos onde os recursos de dados são independentes e presentes em valores booleanos. Multinomial Naive Bayes também é baseado em um modelo baseado em eventos. Possui as características dos dados em forma vetorial, que representam frequências relevantes com base na ocorrência dos eventos.
