25 Perguntas e Respostas da Entrevista de Aprendizado de Máquina - Regressão Linear
Publicados: 2022-09-08É uma prática comum testar aspirantes a ciência de dados em algoritmos de aprendizado de máquina comumente usados em entrevistas. Esses algoritmos convencionais são regressão linear, regressão logística, agrupamento, árvores de decisão etc. Espera-se que os cientistas de dados possuam um conhecimento profundo desses algoritmos.
Consultamos gerentes de contratação e cientistas de dados de várias organizações para saber sobre as perguntas típicas de ML que eles fazem em uma entrevista. Com base em seu extenso feedback, um conjunto de perguntas e respostas foi preparado para ajudar os aspirantes a cientistas de dados em suas conversas. As perguntas da entrevista de regressão linear são as mais comuns em entrevistas de aprendizado de máquina. Perguntas e respostas sobre esses algoritmos serão fornecidas em uma série de quatro postagens no blog.
Melhores cursos de aprendizado de máquina e cursos de IA on-line
| Master of Science em Machine Learning & AI pela LJMU | Programa de Pós-Graduação Executiva em Aprendizado de Máquina e IA do IIITB | |
| Programa de Certificado Avançado em Aprendizado de Máquina e PNL do IIITB | Programa de Certificação Avançado em Aprendizado de Máquina e Aprendizado Profundo do IIITB | Programa Executivo de Pós-Graduação em Ciência de Dados e Aprendizado de Máquina da Universidade de Maryland |
| Para explorar todos os nossos cursos, visite nossa página abaixo. | ||
| Cursos de aprendizado de máquina | ||
Cada postagem do blog abordará o seguinte tópico: -
- Regressão linear
- Regressão Logística
- Agrupamento
- Árvores de decisão e perguntas que pertencem a todos os algoritmos
Vamos começar com a regressão linear!
1. O que é regressão linear?
Em termos simples, a regressão linear é um método para encontrar a melhor linha reta que se ajusta aos dados fornecidos, ou seja, encontrar a melhor relação linear entre as variáveis independentes e dependentes.
Em termos técnicos, a regressão linear é um algoritmo de aprendizado de máquina que encontra a melhor relação de ajuste linear em qualquer dado, entre variáveis independentes e dependentes. É feito principalmente pelo Método da Soma dos Resíduos Quadrados.
Habilidades de aprendizado de máquina sob demanda
| Cursos de Inteligência Artificial | Cursos do Tableau |
| Cursos de PNL | Cursos de Aprendizagem Profunda |

2. Declare as suposições em um modelo de regressão linear.
Existem três suposições principais em um modelo de regressão linear:
- A suposição sobre a forma do modelo:
Assume-se que existe uma relação linear entre as variáveis dependentes e independentes. É conhecido como a 'suposição de linearidade'. - Suposições sobre os resíduos:
- Suposição de normalidade: Assume-se que os termos de erro, ε (i) , são normalmente distribuídos.
- Suposição de média zero: Assume-se que os resíduos têm um valor médio de zero.
- Suposição de variância constante: Supõe-se que os termos residuais têm a mesma (mas desconhecida) variância, σ 2 Essa suposição também é conhecida como suposição de homogeneidade ou homocedasticidade.
- Suposição de erro independente: Assume-se que os termos residuais são independentes uns dos outros, ou seja, sua covariância de pares é zero.
- Suposições sobre os estimadores:
- As variáveis independentes são medidas sem erro.
- As variáveis independentes são linearmente independentes umas das outras, ou seja, não há multicolinearidade nos dados.
Explicação:
- Isso é autoexplicativo.
- Se os resíduos não são normalmente distribuídos, sua aleatoriedade é perdida, o que implica que o modelo não é capaz de explicar a relação nos dados.
Além disso, a média dos resíduos deve ser zero.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Este é o modelo linear assumido, onde ε é o termo residual.
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
Se a expectativa(média) dos resíduos, E(ε (i) ), for zero, as expectativas da variável alvo e do modelo tornam-se as mesmas, que é um dos alvos do modelo.
Os resíduos (também conhecidos como termos de erro) devem ser independentes. Isso significa que não há correlação entre os resíduos e os valores previstos, ou entre os próprios resíduos. Se alguma correlação estiver presente, isso implica que há alguma relação que o modelo de regressão não é capaz de identificar. - Se as variáveis independentes não forem linearmente independentes umas das outras, a unicidade da solução de mínimos quadrados (ou solução de equação normal) é perdida.
Participe do Curso de Inteligência Artificial online das melhores universidades do mundo - Mestrados, Programas de Pós-Graduação Executiva e Programa de Certificado Avançado em ML e IA para acelerar sua carreira.
3. O que é engenharia de recursos? Como aplicá-lo no processo de modelagem?
A engenharia de recursos é o processo de transformar dados brutos em recursos que melhor representam o problema subjacente aos modelos preditivos
, resultando em maior precisão do modelo em dados não vistos.
Em termos leigos, engenharia de recursos significa o desenvolvimento de novos recursos que podem ajudá-lo a entender e modelar o problema de uma maneira melhor. A engenharia de recursos é de dois tipos: orientada a negócios e orientada a dados. A engenharia de recursos orientada a negócios gira em torno da inclusão de recursos do ponto de vista comercial. O trabalho aqui é transformar as variáveis de negócios em características do problema. No caso de engenharia de recursos orientada por dados, os recursos que você adiciona não têm nenhuma interpretação física significativa, mas ajudam o modelo na previsão da variável de destino.
FYI: Curso de PNL grátis!
Para aplicar a engenharia de recursos, é preciso estar totalmente familiarizado com o conjunto de dados. Isso envolve saber quais são os dados fornecidos, o que eles significam, quais são os recursos brutos, etc. Você também deve ter uma ideia clara do problema, como quais fatores afetam a variável de destino, qual é a interpretação física da variável , etc
4. Para que serve a regularização? Explique as regularizações L1 e L2.
A regularização é uma técnica que é usada para resolver o problema de overfitting do modelo. Quando um modelo muito complexo é implementado nos dados de treinamento, ele se sobreajusta. Às vezes, o modelo simples pode não ser capaz de generalizar os dados e o modelo complexo se sobreajusta. Para resolver esse problema, a regularização é usada.
A regularização nada mais é do que adicionar os termos dos coeficientes (betas) à função de custo para que os termos sejam penalizados e tenham magnitude pequena. Isso essencialmente ajuda a capturar as tendências nos dados e, ao mesmo tempo, evita o overfitting ao não deixar o modelo se tornar muito complexo.
- Regularização L1 ou LASSO: Aqui, os valores absolutos dos coeficientes são adicionados à função de custo. Isso pode ser visto na equação a seguir; a parte destacada corresponde à regularização L1 ou LASSO. Essa técnica de regularização fornece resultados esparsos, que também levam à seleção de recursos.
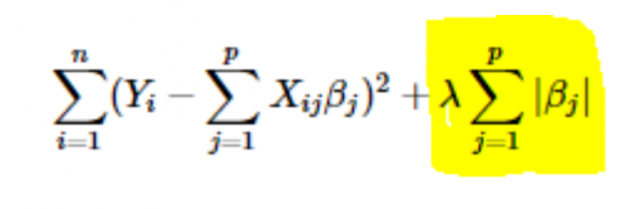
- Regularização L2 ou Ridge: Aqui, os quadrados dos coeficientes são adicionados à função de custo. Isso pode ser visto na equação a seguir, onde a parte destacada corresponde à regularização L2 ou Ridge.
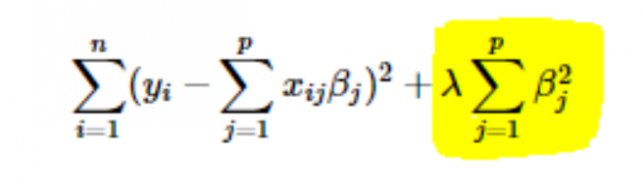
5. Como escolher o valor da taxa de aprendizado do parâmetro (α)?
Selecionar o valor da taxa de aprendizado é um negócio complicado. Se o valor for muito pequeno, o algoritmo de gradiente descendente leva séculos para convergir para a solução ótima. Por outro lado, se o valor da taxa de aprendizado for alto, o gradiente descendente ultrapassará a solução ótima e provavelmente nunca convergirá para a solução ótima.
Para superar esse problema, você pode tentar diferentes valores de alfa em um intervalo de valores e plotar o custo versus o número de iterações. Então, com base nos gráficos, pode-se escolher o valor correspondente ao gráfico que mostra a diminuição rápida. 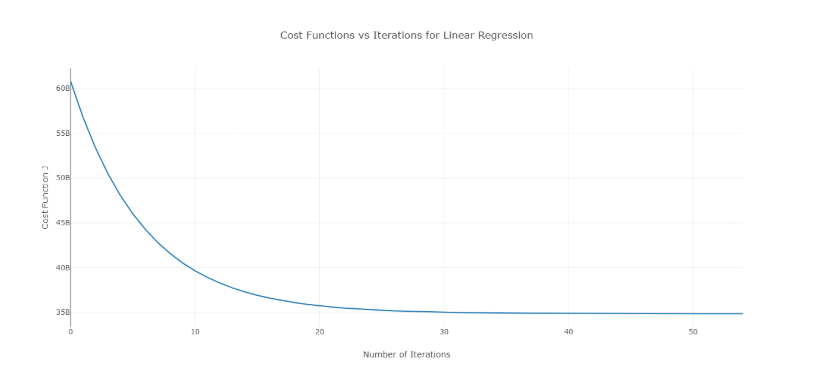
O gráfico mencionado acima é uma curva de custo ideal versus o número de iterações. Observe que o custo inicialmente diminui à medida que o número de iterações aumenta, mas após certas iterações, o gradiente descendente converge e o custo não diminui mais.
Se você perceber que o custo está aumentando com o número de iterações, seu parâmetro de taxa de aprendizado é alto e precisa ser diminuído.
6. Como escolher o valor do parâmetro de regularização (λ)?
Selecionar o parâmetro de regularização é um negócio complicado. Se o valor de λ for muito alto, levará a valores extremamente pequenos do coeficiente de regressão β , o que levará ao underfitting do modelo (alto viés – baixa variância). Por outro lado, se o valor de λ for 0 (muito pequeno), o modelo tenderá a sobreajustar os dados de treinamento (baixo viés – alta variância).
Não existe uma maneira adequada de selecionar o valor de λ . O que você pode fazer é ter uma subamostra de dados e executar o algoritmo várias vezes em conjuntos diferentes. Aqui, a pessoa tem que decidir quanta variação pode ser tolerada. Uma vez que o usuário esteja satisfeito com a variância, esse valor de λ pode ser escolhido para o conjunto de dados completo.
Uma coisa a ser observada é que o valor de λ selecionado aqui foi ótimo para esse subconjunto, não para todos os dados de treinamento.
7. Podemos usar regressão linear para análise de séries temporais?
Pode-se usar regressão linear para análise de séries temporais, mas os resultados não são promissores. Portanto, geralmente não é aconselhável fazê-lo. As razões por trás disso são –
- Os dados de séries temporais são usados principalmente para a previsão do futuro, mas a regressão linear raramente dá bons resultados para a previsão futura, pois não se destina à extrapolação.
- Principalmente, os dados de séries temporais têm um padrão, como durante os horários de pico, épocas festivas, etc., que provavelmente seriam tratados como discrepantes na análise de regressão linear.
8. De que valor se aproxima a soma dos resíduos de uma regressão linear? Justificar.
Ans A soma dos resíduos de uma regressão linear é 0. A regressão linear funciona na suposição de que os erros (resíduos) são normalmente distribuídos com média 0, ou seja
Y = β T X + ε
Aqui, Y é o alvo ou variável dependente,
β é o vetor do coeficiente de regressão,
X é a matriz de recursos contendo todos os recursos como as colunas,
ε é o termo residual tal que ε ~ N(0,σ 2 ).
Assim, a soma de todos os resíduos é o valor esperado dos resíduos vezes o número total de pontos de dados. Como a expectativa de resíduos é 0, a soma de todos os termos residuais é zero.
Nota : N(μ,σ 2 ) é a notação padrão para uma distribuição normal com média μ e desvio padrão σ 2 .
9. Como a multicolinearidade afeta a regressão linear?
Ans A multicolinearidade ocorre quando algumas das variáveis independentes são altamente correlacionadas (positiva ou negativamente) entre si. Essa multicolinearidade causa um problema, pois é contra a suposição básica da regressão linear. A presença de multicolinearidade não afeta a capacidade preditiva do modelo. Portanto, se você deseja apenas previsões, a presença de multicolinearidade não afeta sua saída. No entanto, se você quiser extrair alguns insights do modelo e aplicá-los em, digamos, algum modelo de negócios, isso pode causar problemas.
Um dos principais problemas causados pela multicolinearidade é que ela leva a interpretações incorretas e fornece insights errados. Os coeficientes de regressão linear sugerem a mudança média no valor alvo se uma característica for alterada em uma unidade. Portanto, se existe multicolinearidade, isso não é verdade, pois a alteração de um recurso levará a alterações na variável correlacionada e consequentes alterações na variável de destino. Isso leva a insights errados e pode produzir resultados perigosos para um negócio.
Uma maneira altamente eficaz de lidar com a multicolinearidade é o uso do VIF (Variance Inflation Factor). Quanto maior o valor de VIF para um recurso, mais linearmente correlacionado é esse recurso. Basta remover o recurso com valor VIF muito alto e treinar novamente o modelo no conjunto de dados restante.
10. Qual é a forma normal (equação) da regressão linear? Quando deve ser preferido ao método de gradiente descendente?
A equação normal para regressão linear é -
β=( XTX ) -1 . X T Y
Aqui, Y=β T X é o modelo para a regressão linear,
Y é a variável de destino ou dependente,
β é o vetor do coeficiente de regressão, que é obtido usando a equação normal,
X é a matriz de recursos contendo todos os recursos como as colunas.
Observe aqui que a primeira coluna na matriz X consiste em todos os 1s. Isso é para incorporar o valor de deslocamento para a linha de regressão.
Comparação entre gradiente descendente e equação normal:
| Gradiente descendente | Equação Normal |
| Precisa de ajuste de hiperparâmetro para alfa (parâmetro de aprendizado) | Não há essa necessidade |
| É um processo iterativo | É um processo não iterativo |
| O(kn 2 ) complexidade de tempo | O(n 3 ) complexidade de tempo devido à avaliação de X T X |
| Preferida quando n é extremamente grande | Torna-se bastante lento para grandes valores de n |
Aqui, ' k ' é o número máximo de iterações para gradiente descendente e ' n ' é o número total de pontos de dados no conjunto de treinamento.
Claramente, se tivermos grandes dados de treinamento, a equação normal não é preferida para uso. Para valores pequenos de ' n ', a equação normal é mais rápida que o gradiente descendente.
O que é Machine Learning e por que é importante
11. Você executa sua regressão em diferentes subconjuntos de seus dados e, em cada subconjunto, o valor beta de uma determinada variável varia muito. Qual poderia ser o problema aqui?
Este caso implica que o conjunto de dados é heterogêneo. Portanto, para superar esse problema, o conjunto de dados deve ser agrupado em diferentes subconjuntos e, em seguida, modelos separados devem ser construídos para cada cluster. Outra forma de lidar com esse problema é usar modelos não paramétricos, como árvores de decisão, que podem lidar com dados heterogêneos de forma bastante eficiente.

12. Sua regressão linear não é executada e comunica que há um número infinito de melhores estimativas para os coeficientes de regressão. O que pode estar errado?
Essa condição surge quando há uma correlação perfeita (positiva ou negativa) entre algumas variáveis. Nesse caso, não há valor único para os coeficientes e, portanto, surge a condição dada.
13. O que você entende por R 2 ajustado ? Como é diferente de R 2 ?
R 2 ajustado , assim como R 2 , é um representante do número de pontos ao redor da linha de regressão. Ou seja, mostra quão bem o modelo está se ajustando aos dados de treinamento. A fórmula para R 2 ajustado é -
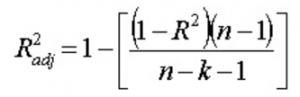
Aqui, n é o número de pontos de dados ek é o número de recursos.
Uma desvantagem de R 2 é que sempre aumentará com a adição de um novo recurso, seja o novo recurso útil ou não. O R 2 ajustado supera essa desvantagem. O valor do R 2 ajustado aumenta apenas se o recurso recém-adicionado desempenhar um papel significativo no modelo.
14. Como você interpreta a curva de valor residual vs valor ajustado?
O gráfico de valor residual vs ajustado é usado para ver se os valores previstos e os resíduos têm uma correlação ou não. Se os resíduos forem distribuídos normalmente, com uma média em torno do valor ajustado e uma variância constante, nosso modelo está funcionando bem; caso contrário, há algum problema com o modelo.
O problema mais comum que pode ser encontrado ao treinar o modelo em um grande intervalo de um conjunto de dados é a heterocedasticidade (isso é explicado na resposta abaixo). A presença de heterocedasticidade pode ser facilmente vista traçando a curva de valor residual versus valor ajustado.
15. O que é heterocedasticidade? Quais são as consequências e como você pode superá-las?
Uma variável aleatória é dita heterocedástica quando diferentes subpopulações têm diferentes variabilidades (desvio padrão).
A existência de heterocedasticidade gera alguns problemas na análise de regressão, pois a suposição diz que os termos de erro não são correlacionados e, portanto, a variância é constante. A presença de heterocedasticidade muitas vezes pode ser vista na forma de um gráfico de dispersão em forma de cone para valores residuais vs ajustados.
Um dos pressupostos básicos da regressão linear é que a heterocedasticidade não está presente nos dados. Devido à violação das premissas, os estimadores de Mínimos Quadrados Ordinários (OLS) não são os Melhores Estimadores Lineares Não Viesados (AZUL). Portanto, eles não fornecem a menor variação do que outros estimadores lineares imparciais (LUEs).
Não existe um procedimento fixo para superar a heterocedasticidade. No entanto, existem algumas maneiras que podem levar a uma redução da heterocedasticidade. Eles são -
- Logaritmizando os dados: Uma série que está aumentando exponencialmente geralmente resulta em maior variabilidade. Isso pode ser superado usando a transformação de log.
- Usando regressão linear ponderada: Aqui, o método OLS é aplicado aos valores ponderados de X e Y. Uma maneira é anexar pesos diretamente relacionados à magnitude da variável dependente.
16. O que é VIF? Como você calcula isso?
O Variance Inflation Factor (VIF) é usado para verificar a presença de multicolinearidade em um conjunto de dados. É calculado como—
Aqui, VIF j é o valor de VIF para a variável j- ésima ,
Rj 2 é o valor de R 2 do modelo quando essa variável é regredida em relação a todas as outras variáveis independentes.
Se o valor de VIF for alto para uma variável, isso implica que o R 2 o valor do modelo correspondente é alto, ou seja, outras variáveis independentes são capazes de explicar aquela variável. Em termos simples, a variável é linearmente dependente de algumas outras variáveis.
17. Como você sabe que a regressão linear é adequada para qualquer dado?
Para ver se a regressão linear é adequada para qualquer dado, um gráfico de dispersão pode ser usado. Se a relação parece linear, podemos optar por um modelo linear. Mas se não for o caso, temos que aplicar algumas transformações para tornar a relação linear. Plotar os gráficos de dispersão é fácil no caso de regressão linear simples ou univariada. Mas no caso de regressão linear multivariada, gráficos de dispersão bidimensionais, gráficos rotativos e gráficos dinâmicos podem ser plotados.
18. Como o teste de hipóteses é usado na regressão linear?
O teste de hipóteses pode ser realizado em regressão linear para os seguintes propósitos:
- Para verificar se um preditor é significativo para a previsão da variável de destino. Dois métodos comuns para isso são:
- Pelo uso de p-valores:
Se o valor-p de uma variável for maior que um determinado limite (geralmente 0,05), a variável é insignificante na previsão da variável alvo. - Verificando os valores do coeficiente de regressão:
Se o valor do coeficiente de regressão correspondente a um preditor for zero, essa variável é insignificante na predição da variável alvo e não tem relação linear com ela.
- Pelo uso de p-valores:
- Verificar se os coeficientes de regressão calculados são bons estimadores dos coeficientes reais.
19. Explique o gradiente descendente em relação à regressão linear.
A descida do gradiente é um algoritmo de otimização. Na regressão linear, ela é utilizada para otimizar a função custo e encontrar os valores dos βs (estimadores) correspondentes ao valor otimizado da função custo.
A descida do gradiente funciona como uma bola rolando em um gráfico (ignorando a inércia). A bola se move ao longo da direção do maior gradiente e para na superfície plana (mínima). 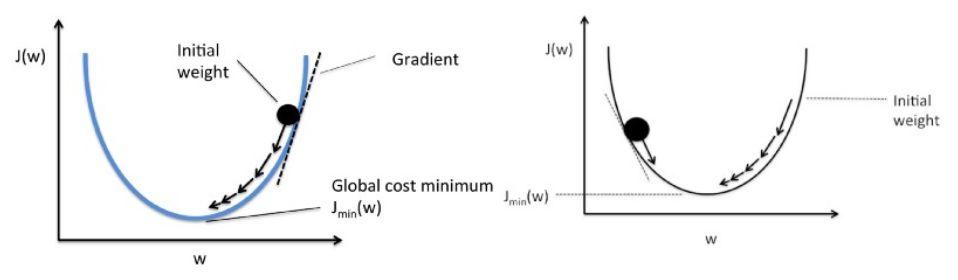
Matematicamente, o objetivo do gradiente descendente para regressão linear é encontrar a solução de
ArgMin J(Θ 0 ,Θ 1 ), onde J(Θ 0 ,Θ 1 ) é a função de custo da regressão linear. é dado por - 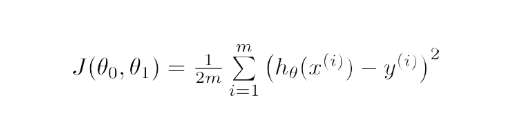
Aqui, h é o modelo de hipótese linear, h=Θ 0 + Θ 1 x, y é a saída verdadeira e m é o número de pontos de dados no conjunto de treinamento.
Gradient Descent começa com uma solução aleatória e, em seguida, com base na direção do gradiente, a solução é atualizada para o novo valor onde a função de custo tem um valor menor.
A atualização é:
Repita até a convergência 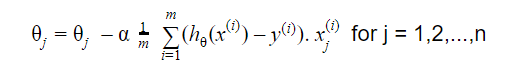
20. Como você interpreta um modelo de regressão linear?
Um modelo de regressão linear é bastante fácil de interpretar. O modelo tem a seguinte forma: 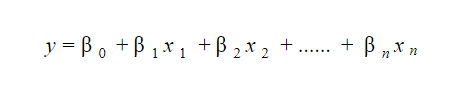
O significado deste modelo reside no fato de que se pode facilmente interpretar e compreender as mudanças marginais e suas consequências. Por exemplo, se o valor de x 0 aumentar em 1 unidade, mantendo as outras variáveis constantes, o aumento total no valor de y será β i . Matematicamente, o termo de interceptação ( β 0 ) é a resposta quando todos os termos preditores são zerados ou não considerados.
Estas 6 técnicas de aprendizado de máquina estão melhorando a saúde
21. O que é regressão robusta?
Um modelo de regressão deve ser robusto por natureza. Isso significa que com mudanças em algumas observações, o modelo não deve mudar drasticamente. Além disso, não deve ser muito afetado pelos outliers.
Um modelo de regressão com OLS (Ordinary Least Squares) é bastante sensível aos outliers. Para contornar este problema, podemos utilizar o método WLS (Weighted Least Squares) para determinar os estimadores dos coeficientes de regressão. Aqui, menos pesos são dados aos outliers ou pontos de alta alavancagem no encaixe, tornando esses pontos menos impactantes.
22. Quais gráficos são sugeridos para serem observados antes do ajuste do modelo?
Antes de ajustar o modelo, deve-se estar bem ciente dos dados, como quais são as tendências, distribuição, assimetria, etc. nas variáveis. Gráficos como histogramas, box plots e dot plots podem ser usados para observar a distribuição das variáveis. Além disso, deve-se analisar também qual é a relação entre variáveis dependentes e independentes. Isso pode ser feito por gráficos de dispersão (no caso de problemas univariados), gráficos rotativos, gráficos dinâmicos, etc.
23. Qual é o modelo linear generalizado?
O modelo linear generalizado é a derivada do modelo de regressão linear comum. O GLM é mais flexível em termos de resíduos e pode ser usado onde a regressão linear não parece apropriada. GLM permite que a distribuição de resíduos seja diferente de uma distribuição normal. Ele generaliza a regressão linear, permitindo que o modelo linear seja vinculado à variável de destino usando a função de vinculação. A estimação do modelo é feita usando o método de estimação de máxima verossimilhança.
24. Explique o trade-off entre viés e variância.
O viés refere-se à diferença entre os valores previstos pelo modelo e os valores reais. É um erro. Um dos objetivos de um algoritmo de ML é ter um viés baixo.
A variância refere-se à sensibilidade do modelo a pequenas flutuações no conjunto de dados de treinamento. Outro objetivo de um algoritmo de ML é ter baixa variância.
Para um conjunto de dados que não é exatamente linear, não é possível ter viés e variância baixos ao mesmo tempo. Um modelo de linha reta terá baixa variância, mas alto viés, enquanto um polinômio de alto grau terá baixo viés, mas alta variância.
Não há como escapar da relação entre viés e variação no aprendizado de máquina.
- Diminuir o viés aumenta a variância.
- Diminuir a variância aumenta o viés.
Portanto, há um trade-off entre os dois; o especialista em ML deve decidir, com base no problema atribuído, quanto viés e variância podem ser tolerados. Com base nisso, o modelo final é construído.
25. Como as curvas de aprendizado podem ajudar a criar um modelo melhor?
As curvas de aprendizado dão a indicação da presença de overfitting ou underfitting.
Em uma curva de aprendizado, o erro de treinamento e o erro de validação cruzada são plotados em relação ao número de pontos de dados de treinamento. Uma curva de aprendizado típica se parece com isso: 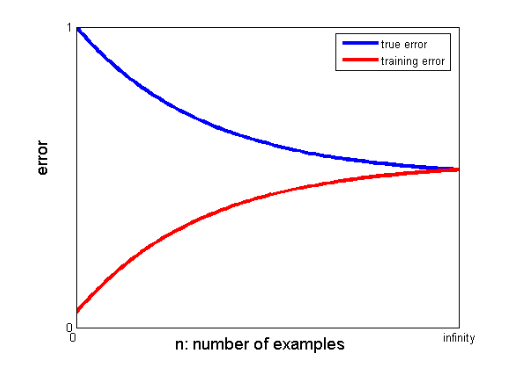
Se o erro de treinamento e o erro verdadeiro (erro de validação cruzada) convergirem para o mesmo valor e o valor correspondente do erro for alto, isso indica que o modelo está subajustado e está sofrendo de alto viés.
Entrevistas de aprendizado de máquina e como aceitá-las
As entrevistas de aprendizado de máquina podem variar de acordo com os tipos ou categorias, por exemplo, alguns recrutadores fazem muitas perguntas de entrevista de regressão linear . Ao optar pela entrevista de Engenheiro de Aprendizado de Máquina, eles podem se especializar em categorias como Codificação, Pesquisa, Estudo de Caso, Gerenciamento de Projetos, Apresentação, Design de Sistema e Estatística. Vamos nos concentrar nos tipos mais comuns de categorias e como se preparar para elas.
- Codificação
A codificação e a programação são componentes importantes de uma entrevista de aprendizado de máquina e são frequentemente usadas para selecionar candidatos. Para se sair bem nessas entrevistas, você precisa ter sólidas habilidades de programação. As entrevistas de codificação geralmente duram de 45 a 60 minutos e são compostas de apenas duas perguntas. O entrevistador apresenta o tema e antecipa que o candidato o abordará no menor tempo possível.
Como se preparar – Você pode se preparar para essas entrevistas tendo uma boa compreensão das estruturas de dados, complexidades de tempo e espaço, habilidades de gerenciamento e capacidade de entender e resolver um problema. O upGrad tem um ótimo curso de engenharia de software que pode ajudá-lo a aprimorar suas habilidades de codificação e a se destacar nessa entrevista.
2. Aprendizado de Máquina
Sua compreensão do aprendizado de máquina será avaliada por meio de entrevistas. Camadas convolucionais, redes neurais recorrentes, redes adversárias generativas, reconhecimento de fala e outros tópicos podem ser abordados dependendo das necessidades de emprego.
Como se preparar – Para ser capaz de aceitar esta entrevista, você deve garantir que tenha um entendimento completo das funções e responsabilidades do trabalho. Isso o ajudará a identificar as especificações do ML que você deve estudar. No entanto, se você não encontrar nenhuma especificação, deve entender profundamente o básico. Um curso aprofundado em ML que o upGrad oferece pode ajudá-lo com isso. Você também pode estudar os artigos mais recentes sobre ML e IA para entender suas últimas tendências e incorporá-los regularmente.
3. Triagem
Esta entrevista é um tanto informal e tipicamente um dos pontos iniciais da entrevista. Um empregador em potencial geralmente lida com isso. O principal objetivo desta entrevista é fornecer ao candidato uma noção do negócio, da função e dos deveres. Em um ambiente mais informal, o candidato também é questionado sobre seu passado para determinar se sua área de interesse corresponde ao cargo.
Como se preparar – Esta é uma parte muito não técnica da entrevista. Tudo isso é necessário é sua honestidade e o básico de sua especialização em Machine Learning.
4. Projeto do Sistema
Essas entrevistas testam a capacidade de uma pessoa de criar uma solução totalmente escalável do início ao fim. A maioria dos engenheiros está tão preocupada com um problema que frequentemente ignora o quadro mais amplo. Uma entrevista de projeto de sistema exige uma compreensão de vários elementos que se combinam para produzir uma solução. Esses elementos incluem o layout de front-end, o balanceador de carga, o cache e muito mais. Um sistema de ponta a ponta eficaz e escalável é mais fácil de desenvolver quando essas questões são bem compreendidas.
Como preparar – Compreender os conceitos e componentes do projeto de design do sistema. Use exemplos da vida real para explicar a estrutura ao seu entrevistador para uma melhor compreensão do projeto.
Blogs populares de aprendizado de máquina e inteligência artificial
| IoT: História, Presente e Futuro | Tutorial de aprendizado de máquina: aprender ML | O que é Algoritmo? Simples e fácil |
| Salário de engenheiro de robótica na Índia: todas as funções | Um dia na vida de um engenheiro de aprendizado de máquina: o que eles fazem? | O que é IoT (Internet das Coisas) |
| Permutação vs Combinação: Diferença entre Permutação e Combinação | As 7 principais tendências em inteligência artificial e aprendizado de máquina | Aprendizado de máquina com R: tudo o que você precisa saber |

Se houver uma lacuna significativa entre os valores convergentes dos erros de treinamento e de validação cruzada, ou seja, o erro de validação cruzada for significativamente maior que o erro de treinamento, isso sugere que o modelo está superajustando os dados de treinamento e está sofrendo de uma alta variância .
Engenheiros de aprendizado de máquina: mitos versus realidades
Esse é o fim da primeira seção desta série. Fique por aqui para a próxima parte da série, que consiste em perguntas baseadas em Regressão Logística . Sinta-se livre para postar seus comentários.
Co-autoria de – Ojas Agarwal
Você pode conferir nosso Programa PG Executivo em Aprendizado de Máquina e IA , que oferece workshops práticos práticos, mentor individual do setor, 12 estudos de caso e atribuições, status de ex-alunos do IIIT-B e muito mais.
O que você entende por regularização?
A regularização é uma estratégia para lidar com o problema de overfitting do modelo. O overfitting ocorre quando um modelo complicado é aplicado aos dados de treinamento. O modelo básico pode não ser capaz de generalizar os dados às vezes, e o modelo complicado pode superajustar os dados. A regularização é usada para aliviar esse problema. Regularização é o processo de adicionar termos de coeficiente (betas) ao problema de minimização de tal forma que os termos sejam penalizados e tenham uma magnitude modesta. Isso essencialmente ajuda na identificação de padrões de dados, ao mesmo tempo em que evita o overfitting, evitando que o modelo se torne muito complexo.
O que você entende sobre engenharia de recursos?
O processo de alteração de dados originais em recursos que melhor descrevem o problema subjacente aos modelos preditivos, resultando em maior precisão do modelo em dados não vistos, é conhecido como engenharia de recursos. Em termos leigos, a engenharia de recursos refere-se à criação de recursos adicionais que podem auxiliar no melhor entendimento e modelagem de um problema. Existem dois tipos de engenharia de recursos: orientada a negócios e orientada a dados. A incorporação de recursos do ponto de vista comercial é o foco da engenharia de recursos voltada para os negócios.
Qual é a compensação viés-variância?
A diferença entre o modelo - valores previstos e os valores reais é chamada de viés. É um erro. Um baixo viés é um dos objetivos de um algoritmo de ML. A vulnerabilidade do modelo a pequenas mudanças no conjunto de dados de treinamento é chamada de variância. A baixa variância é outro objetivo de um algoritmo de ML. É impossível ter baixo viés e baixa variância em um conjunto de dados que não seja perfeitamente linear. A variância de um modelo de linha reta é baixa, mas o viés é grande, enquanto a variância de um polinômio de alto grau é baixa, mas o viés é alto. No aprendizado de máquina, a ligação entre viés e variação é inevitável.
