Introdução à Função de Densidade de Probabilidade [Fórmula, Propriedades, Aplicações, Exemplos]

A Função de Densidade de Probabilidade (PDF) é uma expressão em estatística que denota a distribuição de probabilidade de uma variável aleatória discreta. A distribuição de probabilidade, em termos simples, pode ser definida como a probabilidade de um resultado de uma variável aleatória como uma ação ou um ETF. Variáveis ​​discretas ocorrem em contraste com uma variável aleatória contínua cujo valor exato pode ser determinado.

Por exemplo, o valor de scrip em um mercado de ações tem apenas duas casas decimais (por exemplo, 65,76) em uma variável aleatória discreta em vez de uma variável contínua com qualquer número de casas decimais (exemplo: 65,7685434567).

Uma função de densidade de probabilidade é uma ferramenta estatística usada para determinar a probabilidade do resultado de uma variável aleatória discreta. Quando plotados em um gráfico, os PDFs parecem idênticos a uma curva de sino na qual a área sob a curva representa a probabilidade do resultado.

Quando projetada como um modelo gráfico, a área sob a curva representa a faixa na qual os valores das variáveis ​​aleatórias discretas cairão. Assim, a área total sob a curva é igual à probabilidade do resultado da variável.

A função de densidade de probabilidade pode determinar a probabilidade de uma variável aleatória cair dentro de um intervalo específico de valores.

Normalmente, as funções de densidade de probabilidade analisam os riscos e as receitas potenciais associadas a um fundo específico no mercado de ações.

Condições a serem satisfeitas por uma função a ser considerada uma Função de Densidade de Probabilidade

O valor de uma variável discreta pode ser medido com precisão em contraste com uma variável contínua que pode ter um número infinito de valores. Qualquer função deve satisfazer as duas condições abaixo para ser uma função de densidade de probabilidade:

• O valor de f(x) para cada valor possível da variável aleatória deve ser positivo (não negativo).
• O valor integral da área total da curva (integral de todos os valores possíveis da variável aleatória) deve ser 1.

Diferença entre a Função de Densidade de Probabilidade e a Função de Distribuição de Probabilidade

Variáveis ​​aleatórias podem ter muitos valores. A descrição de cada valor possível que uma variável aleatória pode ter é chamada de distribuição de probabilidade.

A distribuição de probabilidade fornece um conjunto de resultados e suas probabilidades relacionadas. A função estatística que representa uma distribuição de probabilidade contínua é conhecida como função de densidade de probabilidade.

Existe outra ferramenta estatística que representa uma distribuição de probabilidade discreta chamada função de massa de probabilidade. Isso fornece uma descrição detalhada de todos os resultados possíveis e suas probabilidades de probabilidade.

Expressão para Funções de Densidade de Probabilidade

Se a variável aleatória é discreta, sua distribuição de probabilidade é chamada de função de massa de probabilidade e, se for uma variável contínua, a distribuição de probabilidade é chamada de função de densidade de probabilidade.

Um PDF é usado quando a variável aleatória em questão tem um intervalo de valores possíveis. Sua distribuição de probabilidade é usada para determinar o valor exato.

Deixe a variável aleatória ser denotada por X. A função densidade de probabilidade, f da variável aleatória X pode ser expressa como

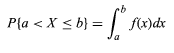
• O valor da variável aleatória está entre a e b.
• Se X denota a probabilidade de selecionar um determinado número do intervalo (intervalo) r e s, então a função densidade de probabilidade pode ser expressa como

f ( x ) = 1/( s − r ) para r < x < sef ( x ) = 0 para x < r ou x > s .

• O PDF F é representado como:

F ( x ) = P { X ≤ x }

que é chamada de função de distribuição ou função de distribuição cumulativa de X.

Considerando que a variável aleatória X tem uma função de distribuição de probabilidade f ( x ), então a relação entre f e F pode ser estabelecida como

F ′(. x ) = f ( x )

A função de distribuição de uma variável aleatória discreta é diferente de sua função de distribuição de probabilidade. A relação entre os dois pode ser expressa da seguinte forma:

A expectativa da variável aleatória é denotada como,

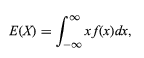
Assim, todas as variáveis ​​discretas e aleatórias podem ser tratadas uniformemente com a ajuda de uma teoria combinada.

A fórmula da Função Densidade de Probabilidade

A probabilidade de uma variável aleatória contínua X em algum valor fixo x é sempre 0. Nesse caso, P(X = x) não pode ser usado. O valor de X situado entre um intervalo de valores (a,b) deve ser determinado. Para determinar o mesmo, a seguinte fórmula é usada.

Propriedades de uma Função de Densidade de Probabilidade

Uma variável aleatória contínua que assume seu valor entre o intervalo (a,b), por exemplo, será estimada calculando a área sob a curva e o eixo X plotado com (a) como seu limite inferior e (b) como seu limite superior. A função de densidade de probabilidade para o acima é representada como:

A função densidade de probabilidade é positiva (não negativa) para todos os valores possíveis. Isso significa que f(x)≥ 0, para todo x. A área que cai entre a curva de densidade e o eixo X (eixo horizontal) é igual a 1.

Isso também pode ser denotado como:

A curva da função densidade é contínua em todo o intervalo dado, que é claramente definido em relação a uma série de valores contínuos ou ao domínio da variável.

Participe do Curso de Aprendizado de Máquina on-line das principais universidades do mundo - Mestrados, Programas de Pós-Graduação Executiva e Programa de Certificado Avançado em ML e IA para acelerar sua carreira.

Aplicações da Função de Densidade de Probabilidade

• A função densidade de probabilidade é utilizada na modelagem anual dos níveis de concentração de NO atmosférico.
• Modelagem da combustão de motores diesel.
• Em estatística, a função densidade de probabilidade é usada para determinar as possibilidades do resultado de uma variável aleatória.

Exemplos de Função de Densidade de Probabilidade

• Exemplo 1

Abaixo está um exemplo de como a função de densidade de probabilidade (PDF) é usada para determinar o potencial de risco de um investidor no mercado de ações:

Primeiro, os PDFs são gerados como uma ferramenta gráfica baseada em informações históricas.

A forma mais comum de PDF é a projeção neutra, onde o risco é igual à recompensa em várias possibilidades. Investidores com menor capacidade de assumir riscos serão recompensados ​​apenas com lucros limitados e, portanto, ficam no lado esquerdo da curva do sino. Por outro lado, os investidores com alta capacidade de assumir riscos provavelmente serão recompensados ​​com rendimentos mais altos e, portanto, se enquadram no lado direito da curva.

A maioria dos investidores se enquadra na capacidade média de tomada de risco e, portanto, ocupa o meio da curva.

Isso ajuda na análise da categoria de investidores com base nos dados recebidos. Isso ajuda os corretores do mercado de ações a identificar sua categoria-alvo de clientes para vender seus produtos.

• Exemplo 2

Uma das aplicações essenciais da função densidade de probabilidade é a variável aleatória gaussiana, também conhecida como variável aleatória normal.

Em ambos os casos, o gráfico fornece uma curva de sino para a função de densidade de probabilidade.

A densidade pode ser expressa como

O gráfico da equação de densidade acima é dado abaixo.

A área sob a curva representa o valor real da variável aleatória gaussiana.

Conclusão

A função de densidade de probabilidade desempenha um papel vital no aprendizado de máquina. Para estudantes que buscam uma carreira em Machine Learning e Inteligência Artificial, é altamente recomendável se inscrever no Programa de Certificação Avançado IIT-Advanced do upGrad em Machine Learning . O programa é personalizado e projetado para equipar profissionais seniores para implantar modelos de aprendizado de máquina usando a tecnologia de computação em nuvem.

O currículo é projetado por professores do IIT Madras e especialistas do setor para tornar o processo de aprendizado mais relevante e prático. O programa oferece certificação reconhecida globalmente da cobiçada e número 1 da faculdade de engenharia na Índia e suporte de colocação de 360 ​​graus do upGrad.

Além disso, você obtém inúmeras oportunidades de colaborar em projetos de grande escala com a base de mais de 40.000 alunos pagos do upGrad.

Acesse nosso site para iniciar sua jornada de aprendizado!