Introdução à regressão multivariada em aprendizado de máquina: guia completo

Não é nenhum segredo que a tecnologia de hoje é orientada por dados. Os dados podem ser apenas uma compilação de números, mas podem ser processados ​​de forma significativa para extrair produtividade e desenvoltura para que as empresas permaneçam competitivas e sustentáveis ​​no longo prazo. Como acontece, a análise de dados é a resposta para derivar estimativas precisas de informações brutas.

A Análise de Dados é uma técnica que envolve ideias estatísticas e lógicas para examinar, processar e transformar dados em uma forma utilizável. As soluções que são desenhadas pela análise de dados são usadas nas empresas para tomar decisões vitais. A ciência de dados, juntamente com a análise de dados, é usada para prever resultados futuros com alta precisão. É um processo de empregar técnicas científicas e algoritmos para obter informações viáveis ​​de um conjunto de dados.

Um problema comum enfrentado pelos profissionais de dados é a maneira de determinar se existe uma relação estatística entre uma variável de resposta (indicada por Y) e variáveis ​​explicativas (indicadas por Xi).

A resposta a esta preocupação é a análise de regressão. Vamos entender isso com mais detalhes.

O que é Análise de Regressão?

A análise de regressão é um dos métodos populares na análise de dados que segue um algoritmo de aprendizado de máquina controlado ou supervisionado. É uma técnica eficaz para identificar e estabelecer uma relação entre variáveis ​​nos dados.

A análise de regressão envolve classificar variáveis ​​viáveis ​​usando estratégias matemáticas para tirar conclusões altamente precisas sobre essas variáveis ​​classificadas.

O que é regressão multivariada?

Multivariado é um algoritmo de aprendizado de máquina controlado ou supervisionado que analisa várias variáveis ​​de dados. É uma continuação da regressão múltipla que envolve uma variável dependente e muitas variáveis ​​independentes. A saída é prevista com base no número de variáveis ​​independentes.

A regressão multivariada descobre uma fórmula que explica a resposta simultânea dos fatores presentes em variáveis ​​às mudanças em outras. Eles são usados ​​para estudar os dados em vários campos. Por exemplo, em imóveis, a regressão multivariada é usada para prever o preço de uma casa com base em vários fatores, como localização, número de quartos e comodidades disponíveis.

Função de custo na regressão multivariada

A função de custo aloca um custo para amostras quando o resultado de um modelo se desvia dos dados observados. A equação da função de custo é o total do quadrado da diferença entre o valor previsto e o valor real dividido por duas vezes o comprimento do conjunto de dados.

Aqui está um exemplo :

Resultado :

Fonte

Como usar a Análise de Regressão Multivariada?

Os processos envolvidos na análise de regressão multivariada incluem a seleção de recursos, engenharia dos recursos, normalização de recursos, funções de perda de seleção, análise de hipóteses e criação de um modelo de regressão.

1. Seleção de características: É o passo mais importante na regressão multivariada. Também conhecido como seleção de variáveis, esse processo envolve a seleção de variáveis ​​viáveis ​​para construir modelos eficientes.
2. Normalização de recursos: envolve o dimensionamento de recursos para manter a distribuição simplificada e as proporções de dados. Isso ajuda na melhor análise de dados. O valor de todos os recursos pode ser alterado de acordo com o requisito.
3. Selecionando a função de perda e hipótese : A função de perda é usada para prever erros. A função de perda entra em jogo quando a previsão da hipótese muda dos números reais. Aqui, a hipótese representa o valor previsto do recurso ou variável.
4. Fixação do parâmetro da hipótese : O parâmetro da hipótese é fixado ou definido de forma a minimizar a função de perda e melhorar a previsão.
5. Reduzindo a função de perda : A função de perda é minimizada gerando um algoritmo específico para minimização de perda no conjunto de dados que por sua vez facilita a alteração dos parâmetros de hipótese. A descida do gradiente é o algoritmo mais comumente usado para minimização de perdas. O algoritmo também pode ser usado para outras ações uma vez que a minimização da perda esteja completa.
6. Analisando a função da hipótese : A função da hipótese precisa ser analisada, pois é crucial para prever os valores. Depois que a função é analisada, ela é testada em dados de teste.

Vejamos agora as duas maneiras pelas quais a regressão multivariada pode ser usada.

1. Regressão Linear Multivariada

A regressão linear multivariada se assemelha à regressão linear simples, exceto que na regressão linear multivariada, múltiplas variáveis ​​independentes contribuem para as variáveis ​​dependentes e, portanto, múltiplos coeficientes são usados ​​no cálculo.

• Ele é usado para derivar uma relação matemática entre várias variáveis ​​aleatórias. Ele explica quantas variáveis ​​independentes múltiplas estão associadas a uma variável dependente.
• Os detalhes das múltiplas variáveis ​​independentes são usados ​​para fazer uma previsão precisa da influência que elas têm na variável de resultado.
• O modelo de regressão linear multivariado gera uma relação de forma linear (uma forma de linha reta) com a melhor aproximação de cada ponto de dados.
• A equação do modelo de regressão linear multivariada é:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

onde para i=n observações:

Fonte

Quando a regressão linear pode ser usada?

O modelo de regressão linear só pode ser utilizado quando existem duas variáveis ​​contínuas das quais uma é dependente e a outra é independente.

A variável independente é usada como parâmetro para determinar o valor ou resultado da variável dependente.

2. Regressão Logística Multivariada

A regressão logística é um algoritmo usado para prever um resultado binário com base em múltiplas variáveis ​​independentes. Um resultado binário tem duas possibilidades, ou o cenário acontece (representado por 1) ou não acontece (indicado por 0).

A regressão logística é usada ao trabalhar com dados binários, os dados em que o resultado (ou a variável dependente) é dicotômico.

Onde a regressão logística pode ser usada?

A regressão logística é usada principalmente para lidar com questões de classificação. Por exemplo, para verificar se um e-mail é spam ou não e se uma determinada transação é maliciosa ou não. Na análise de dados, é usado para tomar decisões calculadas para minimizar as perdas e aumentar os lucros.

A regressão logística multivariada é usada quando há uma variável dependente e vários desfechos. Difere da regressão logística por ter mais de dois resultados possíveis.

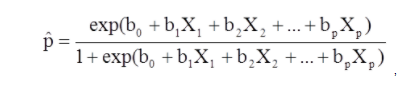
X1 a Xp são variáveis ​​independentes distintas.

b0 a bp são os coeficientes de regressão

O modelo de regressão logística múltipla também pode ser escrito de uma forma diferente. No formulário abaixo, o resultado é o log esperado das chances de que o resultado esteja presente,

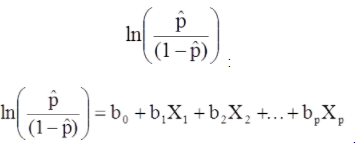
O modelo de regressão logística múltipla também pode ser escrito de uma forma diferente. No formulário abaixo, o resultado é o log esperado das chances de que o resultado esteja presente.

O lado direito da equação acima se assemelha à equação de regressão linear, mas o método de descobrir os coeficientes de regressão é diferente.

Suposições no Modelo de Regressão Multivariada

• As variáveis ​​dependentes e independentes têm uma relação linear.
• As variáveis ​​independentes não possuem correlação forte entre si.
• As observações de yi são escolhidas aleatoriamente e individualmente da população.

Suposições no Modelo de Regressão Logística Multivariada

• A variável dependente é nominal ou ordinal. As variáveis ​​nominais possuem duas ou mais categorias sem qualquer organização significativa. As variáveis ​​ordinais também podem ter duas ou mais categorias, mas possuem uma estrutura e podem ser classificadas.
• Pode haver uma ou várias variáveis ​​independentes que podem ser ordinais, contínuas ou nominais. Variáveis ​​contínuas são aquelas que podem ter valores infinitos dentro de um intervalo específico.
• As variáveis ​​dependentes são mutuamente exclusivas e exaustivas.
• As variáveis ​​independentes não possuem correlação forte entre si.

Vantagens da regressão multivariada

1. A regressão multivariada nos ajuda a estudar as relações entre várias variáveis ​​no conjunto de dados.
2. A correlação entre as variáveis ​​dependentes e independentes auxilia na previsão do desfecho.
3. É um dos algoritmos mais convenientes e populares usados ​​em aprendizado de máquina.

Desvantagens da regressão multivariada

• A complexidade das técnicas multivariadas requer cálculos matemáticos complexos.
• Não é fácil interpretar a saída do modelo de regressão multivariada, pois existem inconsistências nas saídas de perda e erro.
• Modelos de regressão multivariada não podem ser aplicados a conjuntos de dados menores; eles são projetados para produzir resultados precisos quando se trata de conjuntos de dados maiores.

Se você quiser saber mais sobre regressão multivariada e outros assuntos complexos de ciência de dados, o upGrad tem a solução certa para você. Nosso curso de 18 meses de Mestrado em Ciência de Dados da Liverpool John Moores University abrange mais de 500 horas de aprendizado rigorosas, 25 sessões de coaching (realizadas em uma base de 1:8) e mais de 20 sessões ao vivo. O upGrad também oferece assistência de ensino 1:1 e suporte de orientação profissional 360° para que os alunos transformem suas carreiras. Os alunos podem aproveitar o aprendizado ponto a ponto na plataforma global com mais de 40.000 alunos pagos e trabalhar em projetos colaborativos em seis especializações funcionais para maximizar sua experiência de aprendizado.