Descida de gradiente no aprendizado de máquina: como funciona?

Introdução

Uma das partes mais cruciais do Machine Learning é a otimização de seus algoritmos. Quase todos os algoritmos em Machine Learning têm um algoritmo de otimização em sua base que atua como o núcleo do algoritmo. Como todos sabemos, a otimização é o objetivo final de qualquer algoritmo, mesmo com eventos da vida real ou quando se trata de um produto baseado em tecnologia no mercado.

Atualmente, existem muitos algoritmos de otimização que são usados ​​em diversas aplicações, como reconhecimento facial, carros autônomos, análise baseada no mercado, etc. Da mesma forma, em Machine Learning esses algoritmos de otimização desempenham um papel importante. Um desses algoritmos de otimização amplamente utilizado é o algoritmo de descida de gradiente, que abordaremos neste artigo.

O que é Descida Gradiente?

Em Machine Learning, o algoritmo Gradient Descent é um dos algoritmos mais usados ​​e, no entanto, estupefa a maioria dos recém-chegados. Matematicamente, Gradient Descent é um algoritmo de otimização iterativa de primeira ordem que é usado para encontrar o mínimo local de uma função diferenciável. Em termos simples, este algoritmo Gradient Descent é usado para encontrar os valores dos parâmetros de uma função (ou coeficientes) que são usados ​​para minimizar uma função de custo o mais baixo possível. A função de custo é utilizada para quantificar o erro entre os valores previstos e os valores reais de um modelo de Machine Learning construído.

Intuição de descida de gradiente

Considere uma tigela grande com a qual você normalmente guardaria frutas ou comeria cereais. Esta tigela será a função de custo (f).

Agora, uma coordenada aleatória em qualquer parte da superfície da tigela será os valores atuais dos coeficientes da função de custo. O fundo da tigela é o melhor conjunto de coeficientes e é o mínimo da função.

Aqui, o objetivo é calcular os diferentes valores dos coeficientes a cada iteração, avaliar o custo e escolher os coeficientes que possuem um melhor valor de função de custo (menor valor). Em várias iterações, descobrir-se-ia que o fundo da tigela tem os melhores coeficientes para minimizar a função de custo.

Desta forma, o algoritmo Gradient Descent funciona para resultar em custo mínimo.

Participe do Curso de Aprendizado de Máquina on-line das principais universidades do mundo - Mestrados, Programas de Pós-Graduação Executiva e Programa de Certificado Avançado em ML e IA para acelerar sua carreira.

Procedimento de descida de gradiente

Este processo de gradiente descendente começa com a atribuição de valores inicialmente aos coeficientes da função de custo. Isso pode ser um valor próximo a 0 ou um pequeno valor aleatório.

coeficiente = 0,0

Em seguida, obtém-se o custo dos coeficientes aplicando-o à função de custo e calculando o custo.

custo = f(coeficiente)

Em seguida, a derivada da função de custo é calculada. Esta derivada da função custo é obtida pelo conceito matemático de cálculo diferencial. Ela nos dá a inclinação da função no ponto dado onde sua derivada é calculada. Essa inclinação é necessária para saber em qual direção o coeficiente deve ser movido na próxima iteração para obter um valor de custo menor. Isso é feito observando o sinal da derivada calculada.

delta = derivativo(custo)

Uma vez que sabemos qual direção está descendo a derivada calculada, precisamos atualizar os valores dos coeficientes. Para isso, um parâmetro é conhecido como parâmetro de aprendizado, alfa (α) é utilizado. Isso é usado para controlar até que ponto os coeficientes podem mudar a cada atualização.

coeficiente = coeficiente – (alfa * delta)

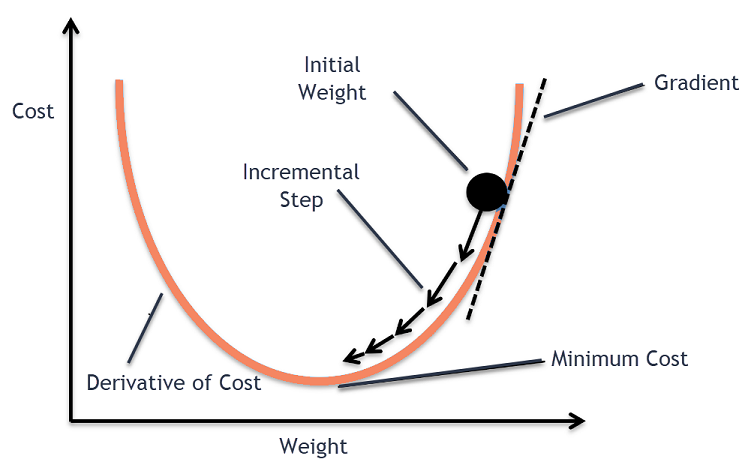
Fonte

Desta forma, este processo é repetido até que o custo dos coeficientes seja igual a 0,0 ou próximo o suficiente de zero. Este é o procedimento para o algoritmo de gradiente descendente.

Tipos de algoritmos de descida de gradiente

Nos tempos modernos, existem três tipos básicos de Gradient Descent que são usados ​​em algoritmos modernos de aprendizado de máquina e aprendizado profundo. A principal diferença entre cada um desses 3 tipos é seu custo computacional e eficiência. Dependendo da quantidade de dados usados, complexidade de tempo e precisão, os seguintes são os três tipos.

1. Descida do gradiente em lote
2. Descida do Gradiente Estocástico
3. Descida de gradiente de mini lote

Descida do gradiente em lote

Esta é a primeira e básica versão dos algoritmos Gradient Descent em que todo o conjunto de dados é usado de uma só vez para calcular a função de custo e seu gradiente. Como todo o conjunto de dados é usado de uma só vez para uma única atualização, o cálculo do gradiente nesse tipo pode ser muito lento e não é possível com os conjuntos de dados que estão fora da capacidade de memória do dispositivo.

Assim, este algoritmo Batch Gradient Descent é usado apenas para conjuntos de dados menores e quando o número de exemplos de treinamento é grande, o batch gradient descendente não é o preferido. Em vez disso, os algoritmos Stochastic e Mini Batch Gradient Descent são usados.

Descida do Gradiente Estocástico

Este é outro tipo de algoritmo de gradiente descendente no qual apenas um exemplo de treinamento é processado por iteração. Neste, o primeiro passo é randomizar todo o conjunto de dados de treinamento. Então, apenas um exemplo de treinamento é usado para atualizar os coeficientes. Isso contrasta com o Batch Gradient Descent em que os parâmetros (coeficientes) são atualizados apenas quando todos os exemplos de treinamento são avaliados.

A Descida do Gradiente Estocástico (SGD) tem a vantagem de que esse tipo de atualização frequente fornece uma taxa detalhada de melhoria. No entanto, em certos casos, isso pode ser computacionalmente caro, pois processa apenas um exemplo a cada iteração, o que pode fazer com que o número de iterações seja muito grande.

Descida de gradiente de mini lote

Este é um algoritmo desenvolvido recentemente que é mais rápido do que os algoritmos Batch e Stochastic Gradient Descent. É principalmente preferido, pois é uma combinação de ambos os algoritmos mencionados anteriormente. Neste, ele separa o conjunto de treinamento em vários mini-lotes e realiza uma atualização para cada um desses lotes após calcular o gradiente desse lote (como no SGD).

Normalmente, o tamanho do lote varia entre 30 e 500, mas não há tamanho fixo, pois variam para diferentes aplicações. Portanto, mesmo que haja um enorme conjunto de dados de treinamento, esse algoritmo o processa em mini-lotes 'b'. Assim, é adequado para grandes conjuntos de dados com um número menor de iterações.

Se 'm' for o número de exemplos de treinamento, então se b==m a Mini Batch Gradient Descent será semelhante ao algoritmo Batch Gradient Descent.

Variantes de descida de gradiente no aprendizado de máquina

Com essa base para Gradient Descent, vários outros algoritmos foram desenvolvidos a partir disso. Alguns deles estão resumidos a seguir.

Descida de gradiente de baunilha

Esta é uma das formas mais simples da Técnica de Descida Gradiente. O nome baunilha significa puro ou sem qualquer adulteração. Neste, pequenos passos são dados na direção dos mínimos calculando o gradiente da função de custo. Semelhante ao algoritmo mencionado acima, a regra de atualização é dada por,

coeficiente = coeficiente – (alfa * delta)

Descida de gradiente com impulso

Nesse caso, o algoritmo é tal que conhecemos os passos anteriores antes de dar o próximo passo. Isso é feito introduzindo um novo termo que é o produto da atualização anterior e uma constante conhecida como momento. Neste, a regra de atualização de peso é dada por,

atualização = alfa * delta

velocidade = atualização_anterior * momento

coeficiente = coeficiente + velocidade – atualização

ADAGRAD

O termo ADAGRAD significa Adaptive Gradient Algorithm. Como o nome diz, ele usa uma técnica adaptativa para atualizar os pesos. Este algoritmo é mais adequado para dados esparsos. Essa otimização altera suas taxas de aprendizado em relação à frequência das atualizações dos parâmetros durante o treinamento. Por exemplo, os parâmetros que possuem gradientes mais altos são feitos para ter uma taxa de aprendizado mais lenta para que não acabemos ultrapassando o valor mínimo. Da mesma forma, gradientes mais baixos têm uma taxa de aprendizado mais rápida para serem treinados mais rapidamente.

ADÃO

Ainda outro algoritmo de otimização adaptativa que tem suas raízes no algoritmo Gradient Descent é o ADAM, que significa Adaptive Moment Estimation. É uma combinação dos algoritmos ADAGRAD e SGD com Momentum. Ele é construído a partir do algoritmo ADAGRAD e é construído ainda mais em desvantagem. Em termos simples ADAM = ADAGRAD + Momentum.

Desta forma, existem várias outras variantes de Algoritmos de Descida de Gradiente que foram desenvolvidos e estão sendo desenvolvidos no mundo como AMSGrad, ADMax.

Conclusão

Neste artigo, vimos o algoritmo por trás de um dos algoritmos de otimização mais usados ​​em Machine Learning, os algoritmos de descida de gradiente, juntamente com seus tipos e variantes que foram desenvolvidos.

O upGrad oferece um Programa PG Executivo em Machine Learning & AI e um Master of Science em Machine Learning & AI que podem orientá-lo na construção de uma carreira. Esses cursos explicarão a necessidade de Machine Learning e outras etapas para reunir conhecimento neste domínio, abrangendo conceitos variados, desde Gradient Descent in Machine Learning.