Gaussian Naive Bayes: O que você precisa saber?
Publicados: 2021-02-22Índice
Gaussiano Naive Bayes
Naive Bayes é um algoritmo de aprendizado de máquina probabilístico usado para muitas funções de classificação e é baseado no teorema de Bayes. Gaussian Naive Bayes é a extensão de Naive Bayes. Enquanto outras funções são usadas para estimar a distribuição de dados, a distribuição gaussiana ou normal é a mais simples de implementar, pois você precisará calcular a média e o desvio padrão para os dados de treinamento.
O que é o Algoritmo Naive Bayes?
Naive Bayes é um algoritmo de aprendizado de máquina probabilístico que pode ser usado em diversas tarefas de classificação. As aplicações típicas do Naive Bayes são classificação de documentos, filtragem de spam, previsão e assim por diante. Este algoritmo é baseado nas descobertas de Thomas Bayes e daí o seu nome.
O nome “Naive” é usado porque o algoritmo incorpora características em seu modelo que são independentes umas das outras. Quaisquer modificações no valor de um recurso não afetam diretamente o valor de qualquer outro recurso do algoritmo. A principal vantagem do algoritmo Naive Bayes é que é um algoritmo simples, mas poderoso.
É baseado no modelo probabilístico onde o algoritmo pode ser codificado facilmente e as previsões feitas rapidamente em tempo real. Portanto, esse algoritmo é a escolha típica para resolver problemas do mundo real, pois pode ser ajustado para responder às solicitações do usuário instantaneamente. Mas antes de mergulharmos profundamente em Naive Bayes e Gaussian Naive Bayes, devemos saber o que se entende por probabilidade condicional.
Probabilidade condicional explicada
Podemos entender melhor a probabilidade condicional com um exemplo. Quando você joga uma moeda, a probabilidade de sair na frente ou sair coroa é de 50%. Da mesma forma, a probabilidade de obter um 4 quando você joga dados com faces é 1/6 ou 0,16.
Se pegarmos um baralho de cartas, qual é a probabilidade de obter uma dama dada a condição de que seja uma espada? Como a condição já está definida de que deve ser uma espada, o denominador ou o conjunto de seleção se torna 13. Há apenas uma rainha de espadas, portanto, a probabilidade de escolher uma rainha de espadas se torna 1/13 = 0,07.

A probabilidade condicional do evento A dado o evento B significa a probabilidade do evento A ocorrer dado que o evento B já ocorreu. Matematicamente, a probabilidade condicional de A dado B pode ser denotada como P[A|B] = P[A AND B] / P[B].
Consideremos um exemplo um pouco complexo. Considere uma escola com um total de 100 alunos. Esta população pode ser demarcada em 4 categorias - Alunos, Professores, Homens e Mulheres. Considere a tabulação abaixo:
| Fêmea | Macho | Total | |
| Professora | 8 | 12 | 20 |
| Aluna | 32 | 48 | 80 |
| Total | 40 | 50 | 100 |
Aqui, qual é a probabilidade condicional de que um certo residente da escola seja um Professor dada a condição de que ele seja um Homem.
Para calcular isso, você terá que filtrar a subpopulação de 60 homens e detalhar os 12 professores do sexo masculino.
Então, a probabilidade condicional esperada P[Professor | Masculino] = 12/60 = 0,2
P (Professor | Masculino) = P (Professor ∩ Masculino) / P (Masculino) = 12/60 = 0,2
Isso pode ser representado como Professor(A) e Masculino(B) dividido por Masculino(B). Da mesma forma, a probabilidade condicional de B dado A também pode ser calculada. A regra que usamos para Naive Bayes pode ser concluída a partir das seguintes notações:
P (A | B) = P (A ∩ B) / P(B)
P (B | A) = P (A ∩ B) / P(A)
A regra de Bayes
Na regra de Bayes, vamos de P (X | Y) que pode ser encontrado no conjunto de dados de treinamento para encontrar P (Y | X). Para conseguir isso, tudo o que você precisa fazer é substituir A e B por X e Y nas fórmulas acima. Para observações, X seria a variável conhecida e Y seria a variável desconhecida. Para cada linha do conjunto de dados, você deve calcular a probabilidade de Y dado que X já ocorreu.
Mas o que acontece quando há mais de 2 categorias em Y? Devemos calcular a probabilidade de cada classe Y para descobrir a vencedora.
Pela regra de Bayes, vamos de P (X | Y) para encontrar P (Y | X)
Conhecido a partir de dados de treinamento: P (X | Y) = P (X ∩ Y) / P(Y)
P (Evidência | Resultado)
Desconhecido - a ser previsto para dados de teste: P (Y | X) = P (X ∩ Y) / P(X)

P (Resultado | Evidência)
Regra de Bayes = P (Y | X) = P (X | Y) * P (Y) / P (X)
Os ingênuos Bayes
A regra de Bayes fornece a fórmula para a probabilidade de Y dada a condição X. Mas no mundo real, pode haver múltiplas variáveis X. Quando você tem recursos independentes, a regra de Bayes pode ser estendida para a regra de Naive Bayes. Os X são independentes um do outro. A fórmula Naive Bayes é mais poderosa que a fórmula Bayes
Gaussiano Naive Bayes
Até agora, vimos que os X estão em categorias, mas como calcular probabilidades quando X é uma variável contínua? Se assumirmos que X segue uma distribuição específica, você pode usar a função de densidade de probabilidade dessa distribuição para calcular a probabilidade de probabilidades.
Se assumirmos que os X seguem uma distribuição gaussiana ou normal, devemos substituir a densidade de probabilidade da distribuição normal e denominá-la Gaussiana Naive Bayes. Para calcular essa fórmula, você precisa da média e da variância de X.
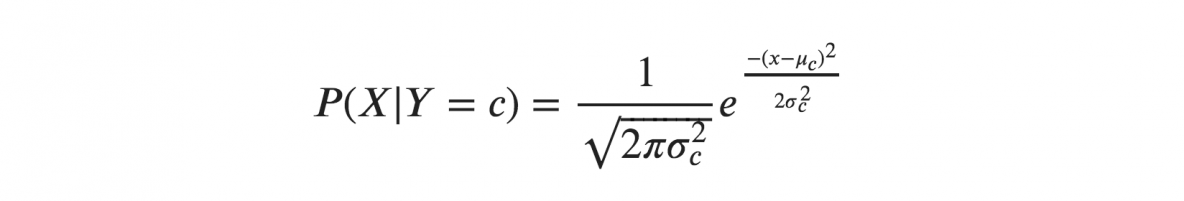
Nas fórmulas acima, sigma e mu é a variância e a média da variável contínua X calculada para uma dada classe c de Y.
Representação para Gaussian Naive Bayes
A fórmula acima calculou as probabilidades de valores de entrada para cada classe por meio de uma frequência. Podemos calcular a média e o desvio padrão de x para cada classe para toda a distribuição.
Isso significa que, juntamente com as probabilidades de cada classe, também devemos armazenar a média e o desvio padrão para cada variável de entrada da classe.
média(x) = 1/n * soma(x)
onde n representa o número de instâncias e x é o valor da variável de entrada nos dados.
desvio padrão(x) = sqrt(1/n * soma(xi-média(x)^2 ))
Aqui a raiz quadrada da média das diferenças de cada x e a média de x é calculada onde n é o número de instâncias, sum() é a função de soma, sqrt() é a função de raiz quadrada e xi é um valor específico de x .

Previsões com o modelo Gaussiano Naive Bayes
A função densidade de probabilidade gaussiana pode ser usada para fazer previsões substituindo os parâmetros pelo novo valor de entrada da variável e, como resultado, a função gaussiana fornecerá uma estimativa para a probabilidade do novo valor de entrada.
Classificador Naive Bayes
O classificador Naive Bayes assume que o valor de uma característica é independente do valor de qualquer outra característica. Classificadores Naive Bayes precisam de dados de treinamento para estimar os parâmetros necessários para a classificação. Devido ao design e aplicação simples, os classificadores Naive Bayes podem ser adequados em muitos cenários da vida real.
Conclusão
O classificador Gaussian Naive Bayes é uma técnica de classificador rápida e simples que funciona muito bem sem muito esforço e com um bom nível de precisão.
Se você estiver interessado em aprender mais sobre IA, aprendizado de máquina, confira o Diploma PG do IIIT-B e do upGrad em aprendizado de máquina e IA, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, Status de ex-aluno do IIIT-B, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.
Aprenda ML Course das melhores universidades do mundo. Ganhe Masters, Executive PGP ou Advanced Certificate Programs para acelerar sua carreira.
O que é um algoritmo ingênuo bayes?
Naive bayes é um algoritmo clássico de aprendizado de máquina. Tendo sua origem na estatística, o naive bayes é um algoritmo simples e poderoso. Naive bayes é uma família de classificadores baseados na aplicação de uma análise de probabilidade condicional. Nesta análise, a probabilidade condicional de um evento é calculada usando a probabilidade de cada um dos eventos individuais que constituem o evento. Os classificadores naive bayes são frequentemente considerados extremamente eficazes na prática, especialmente quando o número de dimensões do conjunto de recursos é grande.
Quais são as aplicações do algoritmo Naive Bayes?
Naive Bayes é usado na classificação de texto, classificação de documentos e indexação de documentos. Em naive bayes, cada recurso possível não tem nenhum peso atribuído na fase de pré-processamento e os pesos são atribuídos posteriormente durante as fases de treinamento e reconhecimento. A suposição básica do algoritmo Naive Bayes é que os recursos são independentes.
O que é o algoritmo Gaussiano Naive Bayes?
Gaussian Naive Bayes é um algoritmo de classificação probabilística baseado na aplicação do teorema de Bayes com fortes hipóteses de independência. No contexto de classificação, independência refere-se à ideia de que a presença de um valor de uma característica não influencia a presença de outra (diferentemente da independência na teoria das probabilidades). Naive refere-se ao uso de uma suposição de que as características de um objeto são independentes umas das outras. No contexto do aprendizado de máquina, os classificadores Bayes ingênuos são conhecidos por serem altamente expressivos, escaláveis e razoavelmente precisos, mas seu desempenho se deteriora rapidamente com o crescimento do conjunto de treinamento. Uma série de recursos contribuem para o sucesso dos classificadores Bayes ingênuos. Mais notavelmente, eles não exigem nenhum ajuste dos parâmetros do modelo de classificação, são bem dimensionados com o tamanho do conjunto de dados de treinamento e podem lidar facilmente com recursos contínuos.
