Derivada da Regra da Cadeia no Aprendizado de Máquina: Explicação

O Machine Learning evoluiu para se tornar um dos campos mais comentados e pesquisados ​​nos anos atuais, e por todas as boas razões. Novos modelos e aplicações de aprendizado de máquina estão sendo descobertos todos os dias, e pesquisadores de todo o mundo estão trabalhando para a próxima grande novidade.

Como resultado, tem havido um interesse crescente em profissionais de diversas origens para mudar para o aprendizado de máquina e fazer parte dessa revolução em andamento. Se você é um desses entusiastas do aprendizado de máquina que deseja dar os primeiros passos, digamos que isso começa com a compreensão dos conceitos básicos de matemática e estatística antes de qualquer outra coisa.

Um desses tópicos vitais em matemática que é altamente relevante para o aprendizado de máquina são os derivados. De sua compreensão básica de cálculo, você deve se lembrar de que a derivada de qualquer função é a taxa instantânea de variação dessa função. Neste blog, vamos nos aprofundar nas derivadas e explorar a regra da cadeia. Veremos como a saída de uma função específica muda quando alteramos algumas variáveis ​​independentes na equação. Com o conhecimento das derivadas da regra da cadeia, você poderá trabalhar na diferenciação de funções mais complexas que certamente encontrará no aprendizado de máquina.

Obtenha a certificação de aprendizado de máquina online das principais universidades do mundo - mestrados, programas de pós-graduação executiva e programa de certificação avançada em ML e IA para acelerar sua carreira.

Entendendo a Derivada da Regra da Cadeia

A regra da cadeia é essencialmente uma fórmula matemática que ajuda a calcular a derivada de uma função composta. Uma função composta é aquela que é composta por duas ou mais funções. Então, se f e g são duas funções, então a regra da cadeia nos ajudaria a encontrar a derivada de funções compostas como fog ou go f.

Considerando a função composta fog, veja como seria a derivada da regra da cadeia:

A regra acima também pode ser escrita como:

Onde a função F é a composição de f e g , na forma de f(g(x)).

Agora, suponha que temos três variáveis ​​tais que a terceira variável (z) depende da segunda variável (y), que por sua vez depende da primeira variável (x). Nesse caso, a derivada da regra da cadeia seria algo assim:

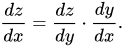Em termos de aprendizado profundo, essa também é a fórmula usada regularmente para resolver problemas de retropropagação. Agora, já que mencionamos que z depende de y e y de x, podemos escrever z = f(y) ey = g(x). Essa substituição modificaria nossa equação diferencial da seguinte maneira:

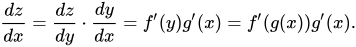Agora, vamos ver alguns exemplos de derivadas da regra da cadeia para entender melhor a matemática por trás delas.

Exemplos e Aplicações da Derivada da Regra da Cadeia

Tomemos um exemplo bem conhecido da Wikipedia para entender melhor a derivada da regra da cadeia. Suponha que você está em queda livre do céu. A pressão atmosférica que você encontra durante a queda continuará mudando constantemente. Aqui está um gráfico que traça esta mudança de pressão atmosférica com níveis de elevação:

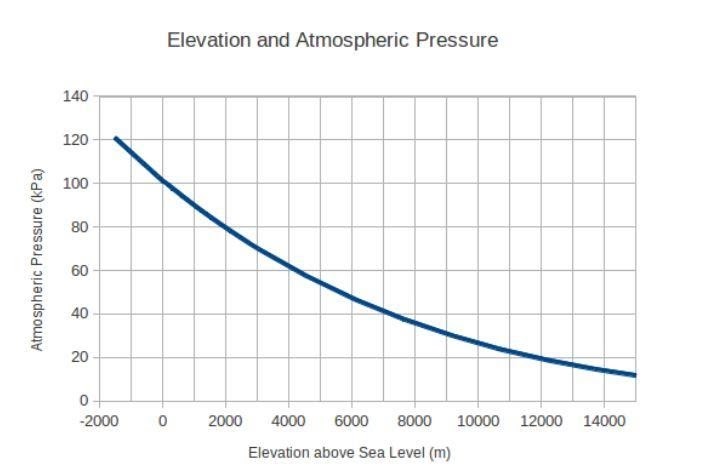
Suponha que sua queda começou a 4.000 metros acima do nível do mar. Inicialmente, sua velocidade era zero e o valor da aceleração era de 9,8 metros por segundo ao quadrado devido à gravidade.

Agora, vamos comparar essa situação com o método anterior da regra da cadeia. Neste exemplo, usaremos a variável 't' para tempo em vez de x.

Então, a variável y = g(t), que informa a distância percorrida desde o início da queda, pode ser dada como:

g(t) = 0,5*9,8t^2

E, a altura do nível do mar pode ser dada por uma variável 'h', que será igual a 400-g(t).

Suponha que, com base em um modelo, também podemos escrever a função da pressão atmosférica em qualquer altura h como:

f(h) = 101325 e−0,0001h

Agora, você pode distinguir entre as duas equações com base em suas variáveis ​​dependentes para obter os seguintes resultados:

g′(t) = −9,8t,

Aqui, g'(t) informa o valor de sua velocidade em qualquer instante t.

f′(h) = −10,1325e−0,0001h

Aqui, f′(h) é a taxa de variação da pressão atmosférica em relação à altura h. Agora, a questão é: podemos combinar essas duas equações e derivar a taxa de variação da pressão atm no tempo? Vamos ver usando a regra da cadeia:

A equação final que temos nos fornece a taxa de variação da pressão atmosférica em relação ao tempo decorrido desde o outono. Em termos de aprendizado de máquina, as redes neurais precisam constantemente de atualizações de peso em relação ao erro do neurônio na previsão. A regra da cadeia ajuda a ajustar esses pesos e aproximar o modelo de aprendizado de máquina da saída correta.

Conclusão

Como você pode ver, a regra da cadeia é benéfica para muitos propósitos. Especialmente quando se trata de aprendizado de máquina ou aprendizado profundo, a regra da cadeia é muito útil na atualização dos pesos dos neurônios e na melhoria da eficiência geral do modelo.

Agora que você está ciente do básico da regra da cadeia, vá em frente e tente alguns problemas por conta própria. Pesquise algumas funções compostas e tente encontrar suas derivadas. Quanto mais você praticar, mais claros seus conceitos ficarão e mais fácil será para você treinar seus modelos de aprendizado de máquina! Dito isso, se você é um entusiasta do aprendizado de máquina, mas está com dificuldades para dar os primeiros passos nesse campo, o upGrad está à sua disposição!

Nosso Executive PG Program in Machine Learning & AI é oferecido em colaboração com o IIIT-Bangalore e oferece a você a escolha de seis especializações relevantes para o setor. O curso começa do nível básico e leva você ao ápice, fornecendo suporte individual de especialistas do setor, um forte grupo de alunos e suporte de carreira de 360 ​​graus.