Estatísticas e Modelo Bayesiano: Explicação

A técnica Bayesiana é uma abordagem em estatística utilizada na análise de dados e estimação de parâmetros. Esta abordagem é baseada no teorema de Bayes.

A Estatística Bayesiana segue um princípio único em que ajuda a determinar a distribuição de probabilidade conjunta para parâmetros observados e não observados usando um modelo estatístico. O conhecimento de estatística é essencial para enfrentar os problemas analíticos neste cenário.

Desde a introdução do teorema de Bayes na década de 1770 por Thomas Bayes, ele permaneceu uma ferramenta indispensável em estatística. Os modelos bayesianos são um substituto clássico para os modelos frequentistas, pois as recentes inovações em estatísticas ajudaram a quebrar marcos em uma ampla gama de indústrias, incluindo pesquisa médica, compreensão de pesquisas na web e processamento de linguagens naturais (Natural Language Processing).

Por exemplo, a doença de Alzheimer é uma doença conhecida por representar um risco progressivo à medida que a pessoa envelhece. No entanto, com a ajuda do teorema de Bayes, os médicos podem estimar a probabilidade de uma pessoa ter Alzheimer no futuro. Também se aplica ao câncer e outras doenças relacionadas à idade às quais uma pessoa se torna vulnerável nos últimos anos de sua vida.

Estatísticas Freqüentes vs Estatísticas Bayesianas

Estatísticas Freqüentes vs Estatísticas Bayesianas tem sido consistentemente um tópico de controvérsia e pesadelos para iniciantes, os quais têm dificuldade em escolher entre os dois. No início do século 20, as estatísticas bayesianas sofreram sua parcela de desconfiança e problemas de aceitação. Com o tempo, no entanto, as pessoas perceberam a aplicabilidade dos modelos bayesianos e as soluções precisas que ele produz.

Veja as estatísticas frequentes e as complexidades associadas a elas:

Estatísticas frequentes

É uma metodologia inferencial amplamente utilizada no mundo da estatística. Ele analisa se um evento (mencionado como hipótese) ocorreu ou não. Ele também estima a probabilidade do evento ocorrer durante o período do experimento. O experimento é repetido até que o resultado desejado seja alcançado.

Suas amostras de distribuição são de tamanho real, e o experimento é repetido infinitas vezes teoricamente. Aqui está um exemplo que mostra como estatísticas frequentes podem ser usadas para estudar o lançamento de uma moeda.

• A possibilidade de obter uma cara ao lançar a moeda uma vez é de 0,5 (1/2).
• O número de cabeças denota o número real de derivações obtidas.
• A diferença entre o número real de caras e o número esperado de caras aumentará à medida que o número de lançamentos aumentar.

Então aqui, o resultado depende do número de vezes que o experimento é repetido. É uma grande desvantagem das estatísticas frequentes.

Outras falhas associadas às suas técnicas de projeto e interpretação tornaram-se evidentes no século 20, quando a aplicação de estatísticas frequentes a modelos numéricos estava no auge.

Limitações das Estatísticas Frequentes

As três principais falhas das estatísticas frequentes estão listadas abaixo:

1. Valores de p variável

Os valores de p medidos para uma amostra com tamanho fixo em um experimento com um ponto final definido mudam com qualquer alteração no ponto final e no tamanho da amostra. Isso resulta em dois valores de p para um único dado que está incorreto.

2. Intervalos de Confiança Inconsistentes

O IC (Intervalo de Confiança) depende exclusivamente do tamanho da amostra. Isso torna o potencial de parada irrelevante.

3. Valores Estimados de CI

Os intervalos de confiança não são uma distribuição de probabilidade e seus valores para um parâmetro são apenas uma estimativa e não valores reais.

As três razões acima deram origem à abordagem Bayesiana que aplica probabilidades a problemas estatísticos.

Nascimento das Estatísticas Bayesianas

O reverendo Thomas Bayes propôs pela primeira vez a abordagem bayesiana à estatística em seu ensaio escrito em 1763. Essa abordagem foi publicada por Richard Price como uma estratégia de probabilidade inversa para prever eventos futuros com base no passado.

A abordagem é baseada no teorema de Bayes que é explicado abaixo:

Teorema de Bayes

O axioma de probabilidade de Renyi examina probabilidades condicionais, onde as possibilidades de ocorrência do evento A e do evento B são dependentes ou condicionais. A probabilidade condicional básica pode ser escrita como:

A probabilidade do evento B ocorrer depende do evento A.

A equação acima é a base da regra de Bayes, uma expressão matemática do teorema de Bayes que afirma:

Aqui, ∩ denota interseção.

A regra de Bayes pode ser escrita como:

A regra de Bayes é a base da estatística Bayesiana, onde as informações disponíveis sobre um determinado parâmetro em um modelo estatístico são comparadas e atualizadas com os dados coletados.

O conhecimento prévio é representado como a distribuição a priori, que é então comparada e estudada com os dados observados ou coletados como uma função de verossimilhança para descobrir a distribuição a posteriori.

Essa distribuição posterior é usada para fazer previsões sobre eventos futuros.

As aplicações da abordagem Bayesiana dependem dos seguintes parâmetros:

1. Definindo o modelo anterior e de dados
2. Fazendo inferências relevantes
3. Analisando e simplificando os modelos

O que são Redes Neurais Bayesianas?

As redes neurais bayesianas (BNNs) são redes que você cria quando estende redes padrão usando a metodologia estatística e altera a inferência posterior para acompanhar o ajuste excessivo. Por se tratar de uma abordagem Bayesiana, existe uma distribuição de probabilidade associada aos parâmetros das redes neurais.

Eles são usados ​​para resolver problemas complexos onde não há um fluxo livre de dados disponível. As redes neurais bayesianas ajudam a controlar o overfitting em domínios como biologia molecular e diagnóstico médico.

Pode-se considerar toda uma distribuição de respostas para uma pergunta em vez de apenas uma possibilidade usando redes neurais bayesianas. Eles ajudam a determinar a seleção/comparação de modelos e a resolver problemas que envolvem regularização.

A estatística bayesiana oferece ferramentas matemáticas para racionalizar e atualizar o conhecimento subjetivo sobre novos dados ou evidências científicas. Ao contrário da abordagem estatística frequente, ela funciona com base na suposição de que as probabilidades dependem da frequência de eventos que se repetem nas mesmas condições.

Em suma, a técnica Bayesiana é uma extensão da suposição e opinião de um indivíduo. O aspecto chave do modelo bayesiano que o torna mais eficiente é o entendimento de que os indivíduos diferem em suas opiniões com base no tipo de informação que recebem.

No entanto, à medida que novas evidências e dados vão surgindo, os indivíduos têm um ponto de convergência, a inferência bayesiana . Essa atualização racional é a característica especial da estatística Bayesiana que a torna mais eficaz em problemas analíticos.

Aqui, a probabilidade de 0 é aplicada quando não há esperança de que um evento ocorra, e a probabilidade de 1 é aplicada quando há certeza de que o evento ocorrerá. Uma probabilidade entre 0 e 1 dá espaço para outros resultados potenciais.

A regra de Bayes agora é aplicada para obter uma inferência Bayesiana para obter uma melhor inferência do modelo.

Como você aplica a regra de Bayes para obter a inferência bayesiana?

Considere a equação:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) denota a distribuição anterior,

P(θ|D) denota a crença posterior,

P(D) representa a evidência,

P(D|θ) indica a probabilidade.

O principal objetivo da inferência bayesiana é oferecer um método racional e matematicamente preciso para combinar as crenças com evidências para obter crenças posteriores atualizadas. As crenças posteriores podem ser usadas como crenças anteriores quando novos dados são gerados. Assim, a inferência bayesiana ajuda a atualizar crenças continuamente com a ajuda da regra de Bayes.

Considerando o mesmo exemplo de lançamento de moedas, o modelo Bayesiano atualiza o procedimento de crenças anteriores para posteriores com novos lançamentos de moedas. O método Bayesiano fornece as seguintes probabilidades.

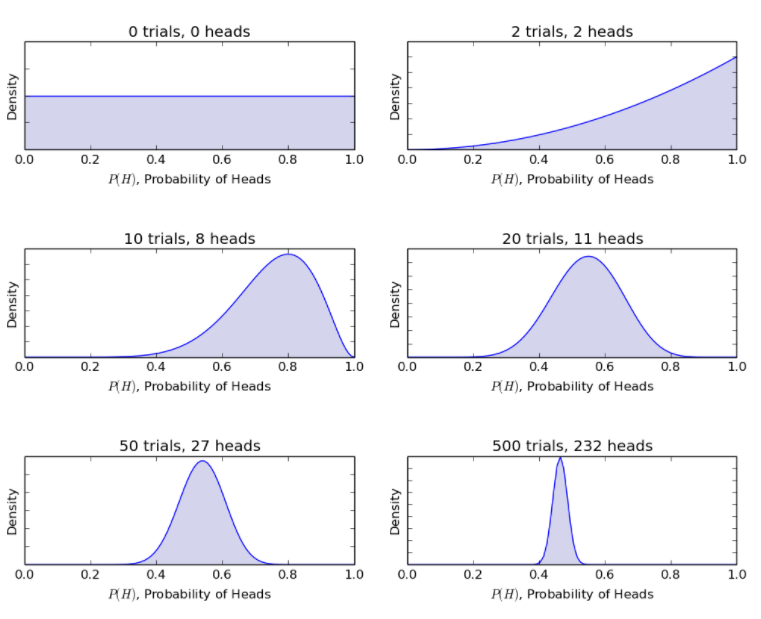
Fonte

Assim, o modelo Bayesiano permite racionalizar um cenário incerto com informações restritas para um cenário mais definido com uma quantidade considerável de dados.

Diferenças notáveis ​​entre o Modelo Bayesiano e o Modelo Frequentista

Estatísticas frequentes

Estatísticas Bayesianas

A meta é considerada como uma estimativa pontual, e o IC

O objetivo é considerado como uma distribuição posterior

O procedimento começa a partir das observações

O processo começa a partir da distribuição prévia

Sempre que novas observações são feitas, a abordagem frequentista recalcula o modelo existente.

Sempre que novas observações são feitas, a distribuição posterior (ideologia/hipótese) é atualizada

Exemplos: Estimativa da média, teste t e ANOVA.

Exemplos: Estimativa da distribuição posterior da média e sobreposição de intervalos de alta densidade.

Vantagens da Estatística Bayesiana

• Ele fornece um meio orgânico e simples de combinar informações pré-concebidas com uma estrutura sólida com evidências científicas. As informações passadas sobre um parâmetro podem ser usadas para formar uma distribuição prévia para investigação futura. As inferências seguem o teorema de Bayes.
• As inferências de um modelo Bayesiano são lógicas e matematicamente precisas e não suposições grosseiras. A precisão permanece constante, independentemente do tamanho da amostra.
• As estatísticas bayesianas seguem o princípio da verossimilhança. Quando duas amostras diferentes têm uma função de verossimilhança comum para uma crença θ, todas as inferências sobre a crença devem ser semelhantes. As técnicas estatísticas clássicas não seguem o princípio da verossimilhança.
• As soluções de uma análise Bayesiana podem ser facilmente interpretadas.
• Ele oferece uma plataforma propícia para vários modelos, como modelos hierárquicos e problemas de dados incompletos. Os cálculos de todos os modelos paramétricos podem ser rastreados virtualmente com a ajuda de outras técnicas numéricas.

Aplicações bem-sucedidas de modelos bayesianos ao longo da história

Os métodos bayesianos tiveram muitas aplicações bem-sucedidas durante a Segunda Guerra Mundial. Alguns deles estão listados abaixo:

• Um estatístico russo, Andrey Kolmogorov , usou com sucesso métodos bayesianos para melhorar a eficiência da artilharia russa.
• Modelos Bayesianos foram usados ​​para quebrar os códigos dos barcos U alemães.
• Um matemático americano nascido na França, Bernard Koopman, ajudou os aliados a identificar a localização dos barcos U alemães com a ajuda de modelos bayesianos para interceptar as transmissões de rádio.

Se você quiser saber mais sobre estatísticas Bayesianas, aqui está a Certificação Avançada em Aprendizado de Máquina e Nuvem do upGrad para entender os conceitos subjacentes por meio de projetos do setor da vida real e estudos de caso. O curso de 12 meses é oferecido pelo IIT Madras e oferece suporte ao aprendizado individualizado.

Entre em contato conosco para mais detalhes.