Exemplo de rede bayesiana [com representação gráfica]

Introdução

Em estatística, os modelos probabilísticos são usados ​​para definir uma relação entre as variáveis ​​e podem ser usados ​​para calcular as probabilidades de cada variável. Em muitos problemas, há um grande número de variáveis. Nesses casos, os modelos totalmente condicionais exigem uma enorme quantidade de dados para cobrir cada caso das funções de probabilidade que podem ser intratáveis ​​para calcular em tempo real. Houve várias tentativas de simplificar os cálculos de probabilidade condicional, como o Naive Bayes, mas ainda assim, não se mostra eficiente, pois reduz drasticamente várias variáveis.

A única maneira é desenvolver um modelo que possa preservar as dependências condicionais entre variáveis ​​aleatórias e a independência condicional em outros casos. Isso nos leva ao conceito de Redes Bayesianas. Essas Redes Bayesianas nos ajudam a visualizar efetivamente o modelo probabilístico para cada domínio e estudar a relação entre variáveis ​​aleatórias na forma de um gráfico amigável.

Aprenda ML Course das melhores universidades do mundo. Ganhe Masters, Executive PGP ou Advanced Certificate Programs para acelerar sua carreira.

O que são Redes Bayesianas?

Por definição, as Redes Bayesianas são um tipo de Modelo Gráfico Probabilístico que utiliza as inferências Bayesianas para cálculos de probabilidade. Representa um conjunto de variáveis ​​e suas probabilidades condicionais com um Gráfico Acíclico Dirigido (DAG). Eles são principalmente adequados para considerar um evento que ocorreu e prever a probabilidade de que qualquer uma das várias possíveis causas conhecidas seja o fator contribuinte.

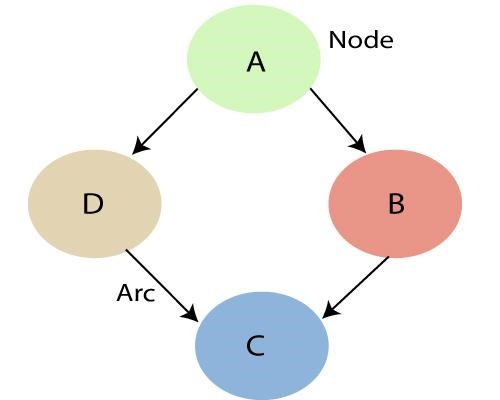
Fonte

Como mencionado acima, fazendo uso das relações especificadas pela Rede Bayesiana, podemos obter a Distribuição de Probabilidade Conjunta (JPF) com as probabilidades condicionais. Cada nó no gráfico representa uma variável aleatória e o arco (ou seta direcionada) representa a relação entre os nós. Eles podem ser contínuos ou discretos por natureza.

No diagrama acima A, B, C e D são 4 variáveis ​​aleatórias representadas por nós dados na rede do gráfico. Para o nó B, A é seu nó pai e C é seu nó filho. O nó C é independente do nó A.

Antes de entrarmos na implementação de uma Rede Bayesiana, existem alguns conceitos básicos de probabilidade que precisam ser entendidos.

Propriedade local de Markov

As Redes Bayesianas satisfazem a propriedade conhecida como Propriedade de Markov Local. Ele afirma que um nó é condicionalmente independente de seus não descendentes, dados seus pais. No exemplo acima, P(D|A, B) é igual a P(D|A) porque D é independente de seu não descendente, B. Essa propriedade nos ajuda a simplificar a Distribuição Conjunta. A Propriedade de Markov Local nos leva ao conceito de Campo Aleatório de Markov que é um campo aleatório em torno de uma variável que se diz seguir as propriedades de Markov.

Probabilidade Condicional

Em matemática, a Probabilidade Condicional do evento A é a probabilidade de que o evento A ocorra, dado que outro evento B já ocorreu. Em termos simples, p(A | B) é a probabilidade do evento A ocorrer, dado que o evento B ocorre. No entanto, existem dois tipos de possibilidades de eventos entre A e B. Eles podem ser eventos dependentes ou eventos independentes. Dependendo do tipo, existem duas maneiras diferentes de calcular a probabilidade condicional.

• Dado que A e B são eventos dependentes, a probabilidade condicional é calculada como P (A| B) = P (A e B) / P (B)
• Se A e B são eventos independentes, então a expressão para probabilidade condicional é dada por, P(A| B) = P (A)

Distribuição Conjunta de Probabilidades

Antes de entrarmos em um exemplo de Redes Bayesianas, vamos entender o conceito de Distribuição de Probabilidade Conjunta. Considere 3 variáveis ​​a1, a2 e a3. Por definição, as probabilidades de todas as diferentes combinações possíveis de a1, a2 e a3 são chamadas de Distribuição de Probabilidade Conjunta.

Se P[a1,a2, a3,….., an] é o JPD das seguintes variáveis ​​de a1 a an, então existem várias maneiras de calcular a Distribuição de Probabilidade Conjunta como uma combinação de vários termos, tais como,

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., an] * P[a2, a3,….., an]

= P[a1 | a2, a3,….., an] * P[a2 | a3,….., um]….P[an-1|an] * P[an]

Generalizando a equação acima, podemos escrever a Distribuição de Probabilidade Conjunta como,

P(X i |X i-1 ,………, X n ) = P(X i | Pais(X i ))

Exemplo de Redes Bayesianas

Vamos agora entender o mecanismo das Redes Bayesianas e suas vantagens com a ajuda de um exemplo simples. Neste exemplo, vamos imaginar que recebemos a tarefa de modelar as notas de um aluno ( m ) para um exame que ele acabou de dar. A partir do gráfico de rede bayesiana fornecido abaixo, vemos que as marcas dependem de duas outras variáveis. Eles estão,

• Nível do Exame ( e )– Esta variável discreta denota a dificuldade do exame e tem dois valores (0 para fácil e 1 para difícil)
• Nível de QI ( i ) – Isso representa o nível do Quociente de Inteligência do aluno e também é de natureza discreta com dois valores (0 para baixo e 1 para alto)

Além disso, o nível de QI do aluno também nos leva a outra variável, que é o Índice de Aptidão do aluno ( s ). Agora, com as notas que o aluno obteve, ele pode garantir a admissão em uma determinada universidade. A distribuição de probabilidade para ser admitido ( a ) em uma universidade também é fornecida abaixo.

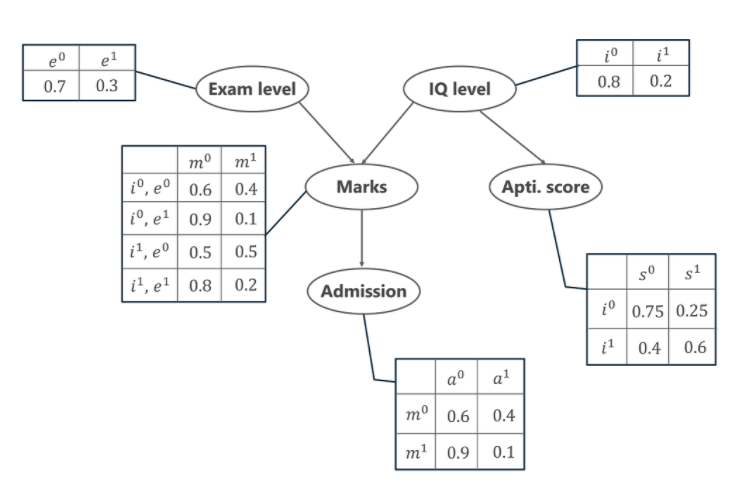
No gráfico acima, vemos várias tabelas representando os valores de distribuição de probabilidade das 5 variáveis ​​dadas. Essas tabelas são chamadas de Tabela de Probabilidades Condicionais ou CPT. Existem algumas propriedades do CPT dadas abaixo –

• A soma dos valores CPT em cada linha deve ser igual a 1 porque todos os casos possíveis para uma determinada variável são exaustivos (representando todas as possibilidades).
• Se uma variável de natureza booleana tem k pais booleanos, então no CPT ela tem 2K valores de probabilidade.

Voltando ao nosso problema, vamos primeiro listar todos os eventos possíveis que estão ocorrendo na tabela acima.

1. Nível do exame (e)
2. Nível de QI (i)
3. Pontuação(s) de Aptidão
4. Marcas (m)
5. Admissão (a)

Essas cinco variáveis ​​são representadas na forma de um Gráfico Acíclico Dirigido (DAG) em formato de Rede Bayesiana com suas tabelas de Probabilidade Condicional. Agora, para calcular a Distribuição de Probabilidade Conjunta das 5 variáveis, a fórmula é dada por,

P[a, m, i, e, s] = P(a | m) . P(m | i, e) . P(i). Educaçao Fisica) . P(s | i)

Da fórmula acima,

• P(a | m) denota a probabilidade condicional de o aluno ser admitido com base nas notas que obteve no exame.
• P(m | i, e) representa as notas que o aluno obterá de acordo com seu nível de QI e dificuldade do nível do exame.
• P(i) e P(e) representam a probabilidade do Nível de QI e do Nível de Exame.
• P(s | i) é a probabilidade condicional da pontuação de aptidão do aluno, dado seu nível de QI.

Com as seguintes probabilidades calculadas, podemos encontrar a Distribuição de Probabilidade Conjunta de toda a Rede Bayesiana.

Cálculo da Distribuição de Probabilidade Conjunta

Vamos agora calcular o JPD para dois casos.

Caso 1: Calcule a probabilidade de que, apesar do nível do exame ser difícil, o aluno com um baixo nível de QI e um baixo Índice de Aptidão consiga passar no exame e garantir a admissão na universidade.

A partir da declaração do problema de palavras acima, a Distribuição de Probabilidade Conjunta pode ser escrita como abaixo,

P[a=1, m=1, i=0, e=1, s=0]

A partir das tabelas de Probabilidade Condicional acima, os valores para as condições fornecidas são alimentados na fórmula e são calculados conforme abaixo.

P[a=1, m=1, i=0, e=0, s=0] = P(a=1 | m=1) . P(m=1 | i=0, e=1) . P(i=0). P(e=1). P(s=0 | i=0)

= 0,1 * 0,1 * 0,8 * 0,3 * 0,75

= 0,0018

Caso 2: Em outro caso, calcule a probabilidade de que o aluno tenha um alto nível de QI e pontuação de aptidão, o exame é fácil, mas não passa e não garante a admissão na universidade.

A fórmula do JPD é dada por

P[a=0, m=0, i=1, e=0, s=1]

Portanto,

P[a=0, m=0, i=1, e=0, s=1]= P(a=0 | m=0) . P(m=0 | i=1, e=0) . P(i=1). P(e=0) . P(s=1 | i=1)

= 0,6 * 0,5 * 0,2 * 0,7 * 0,6

= 0,0252

Assim, desta forma, podemos fazer uso de redes Bayesianas e tabelas de probabilidade para calcular a probabilidade de vários eventos possíveis que ocorrem.

Leia também: Ideias e tópicos de projetos de aprendizado de máquina

Conclusão

Existem inúmeras aplicações para Redes Bayesianas em Filtragem de Spam, Pesquisa Semântica, Recuperação de Informações e muito mais. Por exemplo, com um determinado sintoma, podemos prever a probabilidade de uma doença ocorrer com vários outros fatores que contribuem para a doença. Assim, o conceito de Rede Bayesiana é apresentado neste artigo juntamente com sua implementação com um exemplo da vida real.

Se você está curioso para dominar o aprendizado de máquina e IA, impulsione sua carreira com um curso avançado em aprendizado de máquina e IA com o IIIT-B e a Liverpool John Moores University.