Teorema de Bayes Explicado Com Exemplo - Guia Completo

Introdução

O que é o Teorema de Bayes?

O teorema de Bayes é usado para o cálculo de uma probabilidade condicional onde a intuição muitas vezes falha. Embora amplamente utilizado em probabilidade, o teorema também está sendo aplicado no campo de aprendizado de máquina. Seu uso em aprendizado de máquina inclui o ajuste de um modelo a um conjunto de dados de treinamento e o desenvolvimento de modelos de classificação.

O que é probabilidade condicional?

Uma probabilidade condicional é geralmente definida como a probabilidade de um evento dada a ocorrência de outro evento.

• Se A e B são dois eventos, então a probabilidade condicional pode ser designada como P(A dado B) ou P(A|B).
• A probabilidade condicional pode ser calculada a partir da probabilidade conjunta (A | B) = P(A, B) / P(B)

• A probabilidade condicional não é simétrica; Por exemplo P(A | B) != P(B | A)

Outras formas de calcular a probabilidade condicional incluem o uso de outra probabilidade condicional, ou seja,

P(A|B) = P(B|A) * P(A) / P(B)

O reverso também é usado

P(B|A) = P(A|B) * P(B) / P(A)

Essa forma de cálculo é útil quando é difícil calcular a probabilidade conjunta. Caso contrário, quando a probabilidade condicional reversa está disponível, o cálculo por meio dela se torna fácil.

Esse cálculo alternativo de probabilidade condicional é conhecido como Regra de Bayes ou Teorema de Bayes. É nomeado sob a pessoa que o descreveu pela primeira vez, “Reverendo Thomas Bayes”.

O teorema da fórmula de Bayes

O teorema de Bayes é uma maneira de calcular a probabilidade condicional quando a probabilidade conjunta não está disponível. Às vezes, o denominador não pode ser acessado diretamente. Nesses casos, a forma alternativa de cálculo é:

P(B) = P(B|A) * P(A) + P(B|não A) * P(não A)

Esta é a formulação do teorema de Bayes que mostra um cálculo alternativo de P(B).

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|não A) * P(não A)

A fórmula acima pode ser descrita com colchetes ao redor do denominador

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|não A) * P(não A))

Além disso, se temos P(A), então P(não A) pode ser calculado como

P(não A) = 1 – P(A)

Da mesma forma, se temos P(não B|não A), então P(B|não A) pode ser calculado como

P(B|não A) = 1 – P(não B|não A)

Teorema de Bayes da Probabilidade Condicional

O Teorema de Bayes consiste em vários termos cujos nomes são dados com base no contexto de sua aplicação na equação.

A probabilidade posterior refere-se ao resultado de P(A|B), e a probabilidade anterior refere-se a P(A).

• P(A|B): Probabilidade posterior.
• P(A): Probabilidade anterior.

Da mesma forma, P(B|A) e P(B) são referidos como probabilidade e evidência.

• P(B|A): Probabilidade.
• P(B): Evidência.

Portanto, o teorema de Bayes da probabilidade condicional pode ser reformulado como:

Posterior = Probabilidade * Anterior / Evidência

Se tivermos que calcular a probabilidade de que haja fogo dado que há fumaça, então a seguinte equação será usada:

P(Fogo|Fumaça) = P(Fumaça|Fogo) * P(Fogo) / P(Fumaça)

Onde, P(Fogo) é o Prior, P(Fumaça|Fogo) é a Probabilidade e P(Fumaça) é a evidência.

Uma ilustração do teorema de Bayes

Um exemplo de teorema de Bayes é descrito para ilustrar o uso do teorema de Bayes em um problema.

Problema

Três caixas rotuladas como A, B e C estão presentes. Os detalhes das caixas são:

• A caixa A contém 2 bolas vermelhas e 3 pretas
• A caixa B contém 3 bolas vermelhas e 1 preta
• E a caixa C contém 1 bola vermelha e 4 bolas pretas

Todas as três caixas são idênticas com a mesma probabilidade de serem apanhadas. Portanto, qual é a probabilidade de que a bola vermelha tenha sido retirada da caixa A?

Solução

Seja E o evento em que uma bola vermelha é retirada e A, B e C denotam que a bola é retirada de suas respectivas caixas. Portanto, a probabilidade condicional seria P(A|E) que precisa ser calculada.

As probabilidades existentes P(A) = P(B) = P(C) = 1/3, uma vez que todas as caixas têm a mesma probabilidade de serem escolhidas.

P(E|A) = Número de bolas vermelhas na caixa A / Número total de bolas na caixa A = 2/5

Da mesma forma, P(E|B) = 3/4 e P(E|C) = 1/5

Então evidência P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Portanto, P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Exemplo do Teorema de Bayes

O teorema de Bayes dá a probabilidade de um “evento” com a informação dada em “testes”.

• Há uma diferença entre “eventos” e “testes”. Por exemplo, há um teste para doença hepática, que é diferente de realmente ter a doença hepática, ou seja, um evento.
• Eventos raros podem estar tendo uma taxa de falsos positivos mais alta.

Exemplo 1

Qual é a probabilidade de um paciente ter doença hepática se for alcoólatra?

Aqui, “ser alcoólatra” é o “teste” (tipo de teste decisivo) para doença hepática.

• A é o evento, ou seja, “paciente tem doença hepática””.

De acordo com registros anteriores da clínica, afirma que 10% dos pacientes que entram na clínica sofrem de doença hepática.

Portanto, P(A)=0,10

• B é o teste decisivo de que “Paciente é alcoólatra”.

Registros anteriores da clínica mostraram que 5% dos pacientes que entram na clínica são alcoólatras.

Portanto, P(B)=0,05

• Além disso, 7% dos pacientes que são diagnosticados com doença hepática, são alcoólatras. Isso define o B|A: probabilidade de um paciente ser alcoolista, dado que ele tem uma doença hepática é de 7%.

Como, pela fórmula do teorema de Bayes ,

P(A|B) = (0,07 * 0,1)/0,05 = 0,14

Portanto, para um paciente alcoolista, as chances de ter uma doença hepática são de 0,14 (14%).

Exemplo2

• Incêndios perigosos são raros (1%)
• Mas a fumaça é bastante comum (10%) devido aos churrascos,
• E 90% dos incêndios perigosos produzem fumaça

Qual é a probabilidade de incêndio perigoso quando há fumaça?

Cálculo

P(Fogo|Fumaça) =P(Fogo) P(Fumaça|Fogo)/P(Fumaça)

= 1% x 90%/10%

= 9%

Exemplo 3

Qual a probabilidade de chuva durante o dia? Onde, Chuva significa chuva durante o dia e Nuvem significa manhã nublada.

A chance de Chuva dada a Nuvem é escrita P(Chuva|Nuvem)

P(Chuva|Nuvem) = P(Chuva) P(Nuvem|Chuva)/P(Nuvem)

P(Chuva) é Probabilidade de Chuva = 10%

P(Cloud|Rain) é a Probabilidade de Cloud, dado que Rain acontece = 50%

P(Cloud) é Probabilidade de Cloud = 40%

P(Chuva|Nuvem) = 0,1 x 0,5/0,4 = 0,125

Portanto, uma chance de 12,5% de chuva.

Formulários

Existem várias aplicações do teorema de Bayes no mundo real. As poucas aplicações principais do teorema são:

1. Hipóteses de Modelagem

O teorema de Bayes encontra ampla aplicação no aprendizado de máquina aplicado e estabelece uma relação entre os dados e um modelo. O aprendizado de máquina aplicado usa o processo de teste e análise de diferentes hipóteses em um determinado conjunto de dados.

Para descrever a relação entre os dados e o modelo, o teorema de Bayes fornece um modelo probabilístico.

P(h|D) = P(D|h) * P(h) / P(D)

Onde,

P(h|D): Probabilidade posterior da hipótese

P(h): Probabilidade prévia da hipótese.

Um aumento em P(D) diminui o P(h|D). Por outro lado, se P(h) e a probabilidade de observar os dados da hipótese aumentam, então a probabilidade de P(h|D) aumenta.

2. Teorema de Bayes para Classificação

O método de classificação envolve a rotulagem de um dado dado. Pode ser definido como o cálculo da probabilidade condicional de um rótulo de classe dada uma amostra de dados.

P(classe|dados) = (P(dados|classe) * P(classe)) / P(dados)

Onde P(class|data) é a probabilidade de classe dado os dados fornecidos.

O cálculo pode ser realizado para cada classe. A classe com a maior probabilidade pode ser atribuída aos dados de entrada.

O cálculo da probabilidade condicional não é viável sob condições de um pequeno número de exemplos. Portanto, a aplicação direta do teorema de Bayes não é viável. Uma solução para o modelo de classificação está no cálculo simplificado.

• Classificador Naive Bayes

O teorema de Bayes considera que as variáveis ​​de entrada são dependentes de outras variáveis ​​que causam a complexidade do cálculo. Portanto, a suposição é removida e cada variável de entrada é considerada uma variável independente. Como resultado, o modelo muda de modelo de probabilidade condicional dependente para independente. Em última análise, reduz a complexidade.

Essa simplificação do teorema de Bayes é chamada de Naive Bayes. É amplamente utilizado para classificação e modelos de previsão.

• Classificador ótimo de Bayes

Este é um tipo de modelo probabilístico que envolve a previsão de um novo exemplo dado o conjunto de dados de treinamento. Um exemplo do classificador ótimo de Bayes é "Qual é a classificação mais provável da nova instância, dados os dados de treinamento?"

O cálculo da probabilidade condicional de uma nova instância dados os dados de treinamento pode ser feito através da seguinte equação

P(vj | D) = soma {h em H} P(vj | hi) * P(hi | D)

Onde vj é uma nova instância a ser classificada,

H é o conjunto de hipóteses para classificar a instância,

oi é uma hipótese dada,

P(vj | hi) é a probabilidade posterior para vi dada a hipótese hi, e

P(hi | D) é a probabilidade posterior da hipótese hi dado os dados D.

3. Usos do teorema de Bayes em aprendizado de máquina

A aplicação mais comum do teorema de Bayes em aprendizado de máquina é o desenvolvimento de problemas de classificação. Outras aplicações além da classificação incluem otimização e modelos casuais.

• Otimização Bayesiana

É sempre uma tarefa desafiadora encontrar uma entrada que resulte no custo mínimo ou máximo de uma determinada função objetivo. A otimização bayesiana é baseada no teorema de Bayes e fornece um aspecto para a busca de um problema de otimização global. O método inclui a construção de um modelo probabilístico (função substituta), a busca através de uma função de aquisição e a seleção de amostras candidatas para avaliação da função objetivo real.

No aprendizado de máquina aplicado, a otimização Bayesiana é usada para ajustar os hiperparâmetros de um modelo de bom desempenho.

• Redes Bayesianas de Crenças

As relações entre as variáveis ​​podem ser definidas através do uso de modelos probabilísticos. Eles também são usados ​​para o cálculo de probabilidades. Um modelo de probabilidade totalmente condicional pode não ser capaz de calcular as probabilidades devido ao grande volume de dados. Naive Bayes simplificou a abordagem para o cálculo. Ainda existe outro método onde um modelo é desenvolvido com base na dependência condicional conhecida entre variáveis ​​aleatórias e independência condicional em outros casos. A rede Bayesiana exibe essa dependência e independência através do modelo de grafos probabilísticos com arestas direcionadas. A dependência condicional conhecida é exibida como arestas direcionadas e as conexões ausentes representam as independências condicionais no modelo.

4. Filtragem Bayesiana de Spam

A filtragem de spam é outra aplicação do teorema de Bayes. Dois eventos estão presentes:

• Evento A: A mensagem é spam.
• Teste X: A mensagem contém certas palavras (X)

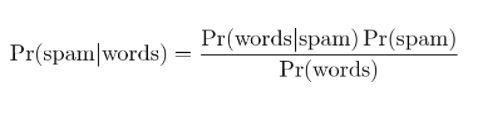
Com a aplicação do teorema de Bayes, pode-se prever se a mensagem é spam dado os “resultados do teste”. Analisar as palavras em uma mensagem pode calcular as chances de ser uma mensagem de spam. Com o treinamento de filtros com mensagens repetidas, atualiza o fato de que a probabilidade de ter determinadas palavras na mensagem seria spam.

Uma aplicação do teorema de Bayes com um exemplo

Um produtor de catalisadores produz um dispositivo para testar defeitos em um determinado eletrocatalisador (EC). O produtor do catalisador afirma que o teste é 97% confiável se o CE estiver com defeito e 99% confiável quando estiver impecável. No entanto, 4% do referido CE pode estar com defeito no momento da entrega. A regra de Bayes é aplicada para verificar a verdadeira confiabilidade do dispositivo. Os conjuntos de eventos básicos são

A : o CE está com defeito; A': o CE é impecável; B: o CE é testado como defeituoso; B': o EC é testado para ser impecável.

As probabilidades seriam

B/A: EC é (conhecido como) defeituoso e testado com defeito, P(B/A) = 0,97,

B'/A: EC é (conhecido por ser) defeituoso, mas testado sem falhas, P(B'/A)=1-P(B/A)=0,03,

B/A': EC é (conhecido como) defeituoso, mas testado com defeito, P(B/A') = 1- P(B'/A')=0,01

B'/A: = EC é (conhecido por ser) impecável e testado sem falhas P(B'/A') = 0,99

As probabilidades calculadas pelo teorema de Bayes são:

A probabilidade de cálculo mostra que há uma alta possibilidade de rejeição de ECs sem falhas (cerca de 20%) e uma baixa possibilidade de identificação de ECs defeituosos (cerca de 80%).

Conclusão

Uma das características mais marcantes de um teorema de Bayes é que a partir de algumas razões de probabilidade, uma enorme quantidade de informação pode ser obtida. Com os meios de verossimilhança, a probabilidade de um evento anterior pode ser transformada em probabilidade posterior. As abordagens do teorema de Bayes podem ser aplicadas nas áreas de estatística, epistemologia e lógica indutiva.

Se você estiver interessado em saber mais sobre o Teorema de Bayes, IA e aprendizado de máquina, confira o Programa PG Executivo do IIIT-B e do upGrad em Machine Learning e IA, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 casos estudos e atribuições, status de ex-alunos do IIIT-B, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.