Czym jest myślenie bayesowskie? Wprowadzenie i twierdzenie

Twierdzenie statystyczne podane przez angielskiego statystyka i filozofa Thomasa Bayesa w XVIII wieku nadal jest światłem przewodnim dla naukowców i analityków na całym świecie. Dzisiaj myślenie bayesowskie znajduje zastosowanie w medycynie, nauce, technologii i kilku innych dyscyplinach i nadal silnie wpływa na nasz światopogląd i wynikające z niego działania.

Pomysł Thomasa Bayesa był uderzająco prosty. Według Bayesa prawdopodobieństwo prawdziwości hipotezy zależy od dwóch warunków: tego, jak racjonalna jest oparta na tym, co już wiemy (wcześniejszej wiedzy) i jak dobrze pasuje do nowych dowodów. Tak więc myślenie bayesowskie różni się od tradycyjnego testowania hipotez tym, że to pierwsze obejmuje wcześniejszą wiedzę przed wyciąganiem pochopnych wniosków.

Mając na uwadze wstępne wprowadzenie, przyjrzyjmy się nieco bardziej szczegółowo statystykom bayesowskim.

Statystyki Bayesa

Mówiąc prościej, statystyki bayesowskie stosują prawdopodobieństwa do problemów statystycznych, aby zaktualizować wcześniejsze przekonania w świetle nowych danych. Prawdopodobieństwo wyraża stopień wiary w określone wydarzenie.

Stopień wiary może opierać się na wcześniejszej wiedzy o zdarzeniu opartej na osobistych założeniach lub wynikach wcześniejszych eksperymentów. Statystyki bayesowskie wykorzystują twierdzenie Bayesa do obliczania prawdopodobieństw. Z kolei twierdzenie Bayesa opisuje warunkowe prawdopodobieństwo zdarzenia w oparciu o nowe dowody i wcześniejsze informacje związane ze zdarzeniem.

Mając to na uwadze, odświeżmy podstawową koncepcję prawdopodobieństwa warunkowego, zanim dogłębnie zrozumiemy twierdzenie Bayesa.

Warunkowe prawdopodobieństwo

Prawdopodobieństwo warunkowe można zdefiniować jako prawdopodobieństwo zdarzenia lub wyniku na podstawie wystąpienia poprzedniego zdarzenia lub wyniku. Oblicza się ją, mnożąc prawdopodobieństwo wcześniejszego zdarzenia przez prawdopodobieństwo późniejszego lub warunkowego zdarzenia.

Rzućmy okiem na przykład, aby lepiej zrozumieć tę koncepcję .

• Wydarzenie A polega na tym, że rodzina planująca wycieczkę pojedzie na piknik. Istnieje 80% szans, że rodzina wybierze się na piknik.
• Wydarzeniem B jest deszcz w dniu, w którym rodzina wyjdzie na piknik. Prognoza pogody mówi, że w dniu pikniku istnieje 60% szans na opady.
• Stąd prawdopodobieństwo (P), że rodzina idzie na piknik i pada deszcz, oblicza się w następujący sposób:

P (piknik i deszcz) = P (deszcz | piknik) P (piknik) = (0,60) * (0,80) = 0,48

W powyższym przykładzie prawdopodobieństwo warunkowe patrzy na dwa zdarzenia A i B w powiązaniu ze sobą, to znaczy prawdopodobieństwo, że rodzina rzeczywiście pójdzie na piknik i pada deszcz tego samego dnia.

W związku z tym prawdopodobieństwo warunkowe różni się od prawdopodobieństwa bezwarunkowego, ponieważ to drugie odnosi się do prawdopodobieństwa wystąpienia zdarzenia niezależnie od tego, czy miało miejsce jakiekolwiek inne zdarzenie lub zdarzenia lub czy występują inne warunki.

Wzór na prawdopodobieństwo warunkowe

Wzór na prawdopodobieństwo warunkowe pochodzi z reguły mnożenia prawdopodobieństwa :

P (A i B) lub P (AUB) = P ( B podane A) lub P (B | A) * P (A)

W powyższym równaniu P (A i B) jest łącznym prawdopodobieństwem, odnoszącym się do prawdopodobieństwa wystąpienia dwóch lub więcej zdarzeń jednocześnie. Jest również pisany jako P (A,B).

Oto jak wyprowadzić warunkowe równanie prawdopodobieństwa z reguły mnożenia:

Krok 1: Zapisz zasadę mnożenia.

P (A i B) = P (B | A) * P (A)

Krok 2: Podziel obie strony równania przez P (A).

P (A i B) / P (A) = P (B | A) * P (A) / P (A)

Krok 3: Anuluj P (A) po prawej stronie równania.

P (A i B) / P (A) = P (B | A)

Krok 4: Przepisz równanie.

P (A i B) = P (B | A) / P (A)

Zatem wzór na prawdopodobieństwo warunkowe jest podany jako:

P (A i B) = P (B | A) / P (A)

Twierdzenie Bayesa

Korzystając z twierdzenia Bayesa, możemy aktualizować nasze przekonania i przekonania na podstawie nowych i odpowiednich dowodów. Na przykład, jeśli próbujemy obliczyć prawdopodobieństwo, że dana osoba ma raka, ogólnie zakładamy, że jest to procent populacji, która ma raka. Jeśli jednak wprowadzimy dodatkowe dowody, na przykład dana osoba jest regularnym palaczem, możemy zaktualizować naszą percepcję (a tym samym prawdopodobieństwo), ponieważ prawdopodobieństwo zachorowania na raka jest wyższe, jeśli dana osoba jest palaczem. Dlatego wykorzystujemy zarówno naszą wcześniejszą wiedzę, jak i dodatkowe dowody, aby poprawić nasze szacunki.

Wzór na twierdzenie Bayesa

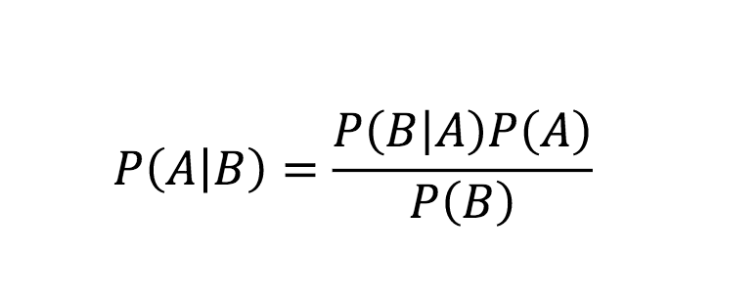
Źródło

Powyższe równanie jest regułą Bayesa. Przyjrzyjmy się teraz stopniowemu wyprowadzaniu równania twierdzenia Bayesa.

Krok 1: Rozważ dwa zdarzenia, A i B. A to zdarzenie, którego prawdopodobieństwo chcemy obliczyć, a B jest dodatkowym dowodem związanym z A.

Krok 2: Zapisz zależność między prawdopodobieństwem łącznym a prawdopodobieństwem warunkowym zdarzeń A i B.

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

Krok 3: Ustaw dwa warunki prawdopodobieństwa warunkowego równe sobie.

P (A | B) * P(B) = P (B | A) * P(A)

Krok 4: Podziel obie strony równania przez P (B).

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

Krok 5: Anuluj P (B) po lewej stronie równania.

P (A | B) = P (B | A) * P(A) / P (B)

W ten sposób otrzymujemy wzór twierdzenia Bayesa w następujący sposób:

P (A | B) = P (B | A) * P(A) / P (B)

Rozumienie terminów w równaniu twierdzenia Bayesa

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B) nazywamy prawdopodobieństwem a posteriori lub prawdopodobieństwem, które próbujemy oszacować. Opierając się na poprzednim przykładzie, prawdopodobieństwo a posteriori byłoby prawdopodobieństwem, że osoba ma raka, biorąc pod uwagę, że osoba ta regularnie pali.
• P (B | A) nazywamy prawdopodobieństwem , odnoszącym się do prawdopodobieństwa wykrycia dodatkowego dowodu, biorąc pod uwagę naszą początkową hipotezę. W powyższym przykładzie prawdopodobieństwo jest prawdopodobieństwem, że dana osoba jest palaczem, biorąc pod uwagę, że dana osoba ma raka.
• P (A) jest prawdopodobieństwem a priori lub prawdopodobieństwem naszej hipotezy bez żadnych dodatkowych dowodów lub informacji. W powyższym przykładzie prawdopodobieństwo a priori to prawdopodobieństwo zachorowania na raka.
• P (B) to marginalne prawdopodobieństwo lub całkowite prawdopodobieństwo zaobserwowania dowodów. W kontekście powyższego przykładu marginalnym prawdopodobieństwem jest prawdopodobieństwo bycia palaczem.

Prosty przykład zrozumienia twierdzenia Bayesa

Używając kilku hipotetycznych liczb w poprzednim przykładzie, zobaczymy efekt zastosowania twierdzenia Bayesa.

Załóżmy, że prawdopodobieństwo zachorowania na raka wynosi 0,06, czyli 6% ludzi ma raka. Teraz powiedzmy, że prawdopodobieństwo bycia palaczem wynosi 0,20 lub 20% osób to palacze, a 30% osób z rakiem to palacze. Tak więc P (palacz | rak) = 0,30.

Początkowo prawdopodobieństwo zachorowania na raka wynosi po prostu 0,06 (przed). Ale korzystając z nowych dowodów, możemy obliczyć P (Rak | Palacz) = P ((Palacz | Rak) * P (Rak)) / P (Palący) = (0,30*0,06) / (0,20) = 0,09.

Ucz się online kursów nauki o danych z najlepszych światowych uniwersytetów. Zdobywaj programy Executive PG, Advanced Certificate Programs lub Masters Programs, aby przyspieszyć swoją karierę.

Dalsza droga: opanuj koncepcje statystyki w karierze w nauce o danych lub uczeniu maszynowym

Platforma edukacyjna upGrad o wyższym poziomie EdTech wpłynęła na ponad 500 000 pracujących profesjonalistów na całym świecie dzięki mnogości kursów i wciągających doświadczeń edukacyjnych. Dzięki ponad 40 000 bazie uczących się w ponad 85 krajach, odpowiednie dla branży kursy upGrad gwarantują rozwój Twojej kariery w wybranej przez Ciebie dziedzinie.

Master of Science in Data Science to 18-miesięczny kurs przekazujący kluczowe umiejętności w zakresie statystyki, analizy predykcyjnej, uczenia maszynowego, analizy Big Data, wizualizacji danych itp.

Najważniejsze punkty programu:

• Tytuł magistra z Liverpool John Moores University i Executive PGP z IIIT Bangalore
• Ponad 500 godzin treści, ponad 60 studiów przypadków i projektów, ponad 20 sesji na żywo, ponad 14 języków programowania i narzędzi
• Nawiązywanie kontaktów branżowych, sesje rozwiązywania wątpliwości i wsparcie edukacyjne

Advanced Certificate Program in Machine Learning i Deep Learning to rygorystyczny 6-miesięczny kurs z możliwościami nawiązywania kontaktów, praktycznymi projektami, mentoringiem branżowym i 360-stopniową pomocą w karierze.

Najważniejsze punkty programu:

• Prestiżowe uznanie od IIIT Bangalore
• Ponad 240 godzin treści, ponad 5 studiów przypadków i projektów, ponad 24 sesje na żywo, pokrycie 12 języków programowania, narzędzi i bibliotek
• Sesje coachingu grupowego 1:8 i sesje mentoringowe 1:1 z ekspertami z branży

Wniosek

Myślenie bayesowskie stanowi podstawę kilku obszarów ludzkiego myślenia, dociekań i wierzeń, chociaż większość z nas nie jest tego świadoma. Od badań przesiewowych w kierunku raka i globalnego ocieplenia po politykę monetarną oraz ocenę ryzyka i ubezpieczenia , myślenie bayesowskie ma fundamentalne znaczenie. Uważa się, że nawet słynny brytyjski matematyk Alan Turing zastosował podejście bayesowskie do złamania niemieckiego kodu Enigmy podczas II wojny światowej.

Zarejestruj się w upGrad i poszerz swoją wiedzę na temat kluczowych pojęć statystycznych i nie tylko!