Pierwsze kroki z ujemną regresją dwumianową: przewodnik krok po kroku

Do modelowania zmiennych liczbowych wykorzystywana jest technika Negatywnej Regresji Dwumianowej. Metoda jest prawie podobna do metody regresji wielokrotnej. Istnieje jednak różnica, że ​​w przypadku ujemnej regresji dwumianowej zmienna zależna, tj. Y, podąża za ujemnym rozkładem dwumianowym. Dlatego wartości zmiennej mogą być nieujemnymi liczbami całkowitymi, takimi jak 0, 1, 2.

Metoda jest również rozszerzeniem regresji Poissona, która powoduje rozluźnienie przy założeniu, że średnia jest równa wariancji. Jeden z tradycyjnych modeli regresji dwumianowej, zdefiniowany jako „NB2”, oparty jest na mieszanym rozkładzie Poissona-gamma.

Metoda regresji Poissona jest uogólniona poprzez dodanie zmiennej szumu gamma. Ta zmienna ma wartość średnią 1, a także parametr skali, którym jest „v”.

Oto kilka przykładów negatywnej regresji dwumianowej:

• Dyrekcja szkoły przeprowadziła badanie w celu zbadania zachowań frekwencyjnych uczniów szkół ponadgimnazjalnych z dwóch szkół. Czynnikami, które mogą wpływać na zachowanie frekwencji, mogą być dni, w których juniorzy byli nieobecni w szkole. Również program, do którego zostali zapisani.
• Badacz z badania dotyczącego zdrowia przeprowadził badanie, ilu seniorów odwiedziło szpital w ciągu ostatnich 12 miesięcy. Badanie opierało się na cechach jednostki i planach zdrowotnych zakupionych przez seniorów.

Przykład negatywnej regresji dwumianowej

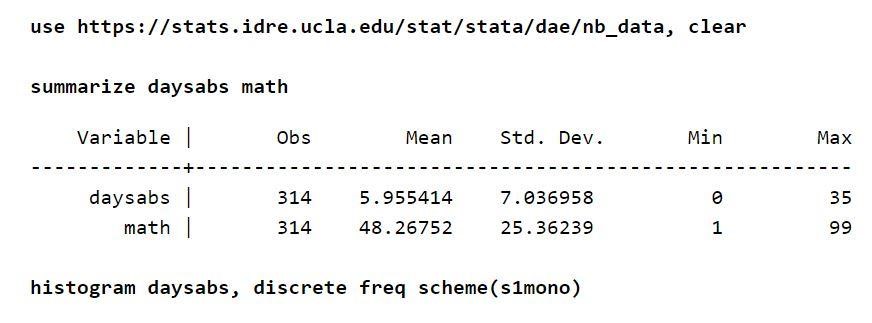
Załóżmy, że istnieje lista obecności około 314 uczniów ze szkoły średniej. Dane są pobierane z dwóch szkół miejskich i przechowywane w pliku o nazwie nb_data.dta. Interesującą zmienną odpowiedzi w tym przykładzie są dni nieobecności, które są „dniami abs”. Obecna jest jedna zmienna „matematyka”, która definiuje wynik z matematyki dla każdego ucznia. Jest jeszcze inna zmienna, którą jest „prog”. Ta zmienna wskazuje program, do którego zapisani są studenci.

Źródło

Każda ze zmiennych ma około 314 obserwacji. Dlatego rozkłady między zmiennymi są również rozsądne. Również biorąc pod uwagę zmienną wynikową, bezwarunkowa średnia jest niższa niż wariancja.

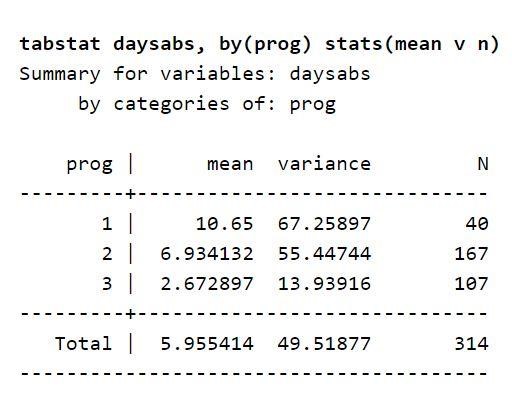
Teraz skup się na opisie zmiennej uwzględnionym w zbiorze danych. Tabela zawiera zestawienie średniej liczby dni nieobecności ucznia w szkole w każdym typie programu. Sugeruje to, że program typu zmiennego może przewidzieć dni nieobecności ucznia w szkole. Możesz go również użyć do przewidywania zmiennej wynikowej. Dzieje się tak, ponieważ średnia wartość zmiennej wynikowej różni się w zależności od zmiennej prog. Ponadto wartości wariancji są wyższe niż na każdym poziomie progu zmiennej. Wartości te nazywane są wariancjami i średnimi. Istniejące różnice sugerują, że istnieje nadmierna dyspersja, dlatego właściwe będzie zastosowanie ujemnego modelu dwumianowego.

Źródło

Badacz może rozważyć kilka metod analizy tego typu badań. Metody te opisano poniżej. Kilka metod analizy, które użytkownik może wykorzystać do analizy modelu regresji, to:

1. Negatywna regresja dwumianowa

Metodę negatywnej regresji dwumianowej należy stosować, gdy dane są nadmiernie rozproszone. Oznacza to, że wartość wariancji warunkowej jest większa lub przekracza wartość średniej warunkowej. Metodę uważa się za uogólnioną z metody regresji Poissona. Dzieje się tak, ponieważ obie metody mają tę samą strukturę średniej. Istnieje jednak dodatkowy parametr w ujemnej regresji dwumianowej, używany do modelowania nadmiernej dyspersji. Przedziały ufności są uważane za węższe niż regresja pasji, gdy rozkład warunkowy jest nadmiernie rozproszony od zmiennej wynikowej.

2. Regresja Poissona

W modelowaniu danych zliczanych wykorzystywana jest metoda regresji Poissona. Wiele rozszerzeń można wykorzystać do modelowania zmiennych liczebności w regresji Poissona.

3. Regresja OLS

Wyniki zmiennych liczebności są czasami przekształcane logarytmicznie, a następnie analizowane metodą regresji OLS. Czasami jednak pojawiają się problemy związane z metodą regresji OLS. Problemy te mogą dotyczyć utraty danych z powodu wygenerowania dowolnej nieokreślonej wartości poprzez uwzględnienie dziennika wartości zero. Może być również generowany ze względu na brak modelowania rozproszonych danych.

4. Modele z zerowym napompowaniem

Tego typu modele starają się uwzględnić wszystkie nadmiarowe zera w modelu.

Analiza za pomocą ujemnej regresji dwumianowej

Polecenie „nbreg” służy do estymacji modelu ujemnej regresji dwumianowej. Przed zmienną „prog” znajduje się „i”. Obecność „i” wskazuje, że zmienna jest typu factor, tj. zmienna kategorialna. Należy je uwzględnić jako zmienne wskaźnikowe w modelu.

• Dane wyjściowe modelu zaczynają się od dziennika iteracji. Zaczyna się od dopasowania modelu Poissona, następnie modelu zerowego, a następnie modelu dwumianu ujemnego. Metoda wykorzystuje oszacowanie największej prawdopodobieństwa i kontynuuje iterację aż do zmiany wartości końcowego logu. Do porównania modeli wykorzystuje się prawdopodobieństwo dziennika.
• Kolejne informacje znajdują się w pliku nagłówkowym.
• Tuż pod nagłówkiem znajduje się informacja o współczynnikach ujemnej regresji dwumianowej. Współczynniki są generowane dla każdej zmiennej wraz z błędami, takimi jak wartości p, z-score. Dla wszystkich współczynników istnieje również przedział ufności wynoszący 95%. Współczynnik dla zmiennej „matematyka” wynosi -0,006, co oznacza, że ​​jest ona istotna statystycznie. Wynik oznacza, że ​​jeśli nastąpi wzrost o jedną jednostkę na zmiennej „matematyka”, oczekiwana liczba logów dla nieobecnej liczby dni zmniejsza się o wartość 0,006. Również wartość 2. prog, zmiennej wskaźnikowej, jest oczekiwaną różnicą w liczbie log między dwiema grupami (grupą 2 i grupą odniesienia).
• Estymacja parametrów dla logarytmu przenoszonej naddyspersji jest wykonywana, a następnie wyświetlana z nieprzekształconą wartością. W modelu Poissona wartość wynosi zero.
• Poniżej tabeli współczynników znajduje się informacja o prawdopodobieństwie testu współczynnika. Model można lepiej zrozumieć za pomocą poleceń „marginesy”.

Proces wykonywania negatywnej analizy regresji dwumianowej w Pythonie

Wymagane pakiety do przeprowadzenia procesu regresji muszą zostać zaimportowane z Pythona. Te pakiety są wymienione poniżej:

• importuj statsmodels.api jako sm
• importuj matplotlib.pyplot jako plt
• importuj numer jako np
• z patsy import dmatrices
• importuj pandy jako PD

Rozważania dotyczące negatywnej regresji dwumianowej

Jest kilka rzeczy, które należy wziąć pod uwagę, stosując metodę analizy ujemnej regresji dwumianowej. Obejmują one:

• W przypadku obecności małych próbek nie zaleca się stosowania metody ujemnej regresji dwumianowej.
• Czasami występują nadmiarowe zera, które mogą być przyczyną nadmiernej dyspersji. Te zera mogą być generowane w wyniku procesu dodawania generowania danych. W przypadku wystąpienia tego typu przypadku, zaleca się zastosowanie metody modelu napompowanego do zera.
• Jeżeli proces generowania danych nie uwzględnia żadnych zer, to w takich przypadkach zaleca się zastosowanie metody modelu z obciętymi zerami.
• Z danymi zliczania związana jest zmienna ekspozycji. Zmienna oznacza czasy, w których istnieje prawdopodobieństwo wystąpienia zdarzenia. Ta zmienna jest konieczna do włączenia do modelu ujemnej regresji dwumianowej. Odbywa się to za pomocą opcji exp().
• Zmienna wynikowa nie może być żadną wartością ujemną w modelu analizy negatywnej regresji dwumianowej. Ponadto zmienna ekspozycji nie może mieć wartości 0.
• Polecenia „glm” można również użyć do uruchomienia metody analizy ujemnej regresji dwumianowej. Można to zrobić za pomocą łącza dziennika, a także rodziny dwumianów.
• Do uzyskania reszt wymagane jest polecenie „glm”. Ma to na celu sprawdzenie, czy w modelu negatywnej regresji dwumianowej istnieją jakiekolwiek inne założenia.
• Istnieją różne miary pseudo-R-kwadrat. Jednak każda miara dostarcza informacji podobnych do informacji dostarczanych przez R-kwadrat w regresji OLS.

Wniosek

W artykule omówiono temat negatywnej regresji dwumianowej . Widzieliśmy, że jest ona prawie podobna do metody regresji wielokrotnych i jest uogólnioną formą rozkładu Poissona. Istnieje kilka zastosowań tej metody. Technikę tę można również zastosować za pośrednictwem języka programowania Python lub R.

Istnieje również kilka studiów przypadku, które pokazują jego zastosowanie w badaniach takich jak starzenie się. Ponadto klasycznymi modelami regresji, które można zastosować do danych liczbowych, są regresja Poissona, ujemna regresja dwumianowa i regresja geometryczna. Metody te należały do ​​rodziny modeli liniowych i były zawarte w prawie wszystkich pakietach statystycznych, takich jak system R.

Jeśli chcesz doskonalić się w uczeniu maszynowym i chcesz zgłębić dziedzinę danych, możesz sprawdzić kurs Executive PG Program in Machine Learning & AI oferowany przez upGrad. Tak więc, jeśli jesteś pracującym profesjonalistą, który marzy o byciu ekspertem w dziedzinie uczenia maszynowego, przyjdź i zdobądź doświadczenie w szkoleniu pod okiem ekspertów. Więcej szczegółów można uzyskać za pośrednictwem naszej strony internetowej. W przypadku jakichkolwiek pytań nasz zespół może Ci szybko pomóc.

Zwiększ swoją karierę w uczeniu maszynowym i sztucznej inteligencji

Złóż wniosek o certyfikat dla kadry kierowniczej w Ai-ml z IIITB