25 pytań i odpowiedzi na wywiad dotyczący uczenia maszynowego – regresja liniowa
Opublikowany: 2022-09-08Powszechną praktyką jest testowanie kandydatów do nauki o danych na powszechnie używanych algorytmach uczenia maszynowego podczas wywiadów. Te konwencjonalne algorytmy to regresja liniowa, regresja logistyczna, grupowanie, drzewa decyzyjne itp. Oczekuje się, że naukowcy zajmujący się danymi będą posiadać dogłębną wiedzę na temat tych algorytmów.
Skonsultowaliśmy się z menedżerami ds. rekrutacji i analitykami danych z różnych organizacji, aby poznać typowe pytania dotyczące ML, które zadają podczas wywiadu. Na podstawie ich obszernych informacji zwrotnych przygotowano zestaw pytań i odpowiedzi, aby pomóc początkującym naukowcom danych w ich rozmowach. Pytania podczas wywiadu opartego na regresji liniowej są najczęściej spotykane w przypadku wywiadów dotyczących uczenia maszynowego. Pytania i odpowiedzi dotyczące tych algorytmów zostaną przedstawione w serii czterech wpisów na blogu.
Najlepsze kursy online na temat uczenia maszynowego i sztucznej inteligencji
| Master of Science in Machine Learning & AI od LJMU | Program studiów podyplomowych dla kadry kierowniczej w zakresie uczenia maszynowego i sztucznej inteligencji z IIITB | |
| Zaawansowany program certyfikacji w uczeniu maszynowym i NLP z IIITB | Zaawansowany program certyfikacji w uczeniu maszynowym i uczeniu głębokim z IIITB | Executive Post Graduate Program in Data Science & Machine Learning z University of Maryland |
| Aby poznać wszystkie nasze kursy, odwiedź naszą stronę poniżej. | ||
| Kursy na temat uczenia maszynowego | ||
Każdy post na blogu będzie dotyczył następującego tematu:-
- Regresja liniowa
- Regresja logistyczna
- Grupowanie
- Drzewa decyzyjne i pytania dotyczące wszystkich algorytmów
Zacznijmy od regresji liniowej!
1. Co to jest regresja liniowa?
W uproszczeniu regresja liniowa to metoda znalezienia najlepszej linii prostej pasującej do danych, czyli znalezienia najlepszej zależności liniowej między zmienną niezależną i zmienną zależną.
Z technicznego punktu widzenia regresja liniowa to algorytm uczenia maszynowego, który znajduje najlepszą relację dopasowania liniowego dla dowolnych danych, między zmiennymi niezależnymi i zależnymi. Odbywa się to głównie metodą sumy kwadratów reszt.
Umiejętności uczenia maszynowego na żądanie
| Kursy sztucznej inteligencji | Kursy Tableau |
| Kursy NLP | Kursy głębokiego uczenia się |

2. Podaj założenia w modelu regresji liniowej.
W modelu regresji liniowej istnieją trzy główne założenia:
- Założenie o formie modelu:
Zakłada się, że istnieje liniowa zależność między zmienną zależną i niezależną. Jest to znane jako „założenie liniowości”. - Założenia dotyczące reszt:
- Założenie normalności: Zakłada się, że składniki błędu, ε (i) , mają rozkład normalny.
- Założenie zerowej średniej: Zakłada się, że reszty mają średnią wartość równą zero.
- Założenie o stałej wariancji: Zakłada się, że człony resztowe mają taką samą (ale nieznaną) wariancję, σ 2 Założenie to jest również znane jako założenie homogeniczności lub homoskedastyczności.
- Założenie o niezależnym błędzie: Zakłada się, że składniki resztowe są od siebie niezależne, tj. ich kowariancja parami wynosi zero.
- Założenia dotyczące estymatorów:
- Zmienne niezależne są mierzone bez błędu.
- Zmienne niezależne są od siebie liniowo niezależne, tzn. nie ma współliniowości danych.
Wyjaśnienie:
- To nie wymaga wyjaśnień.
- Jeśli reszty nie mają rozkładu normalnego, ich losowość jest tracona, co oznacza, że model nie jest w stanie wyjaśnić zależności w danych.
Również średnia reszt powinna wynosić zero.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Jest to założony model liniowy, gdzie ε jest członem rezydualnym.
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
Jeśli oczekiwanie (średnia) reszt, E(ε (i) ), wynosi zero, oczekiwania zmiennej docelowej i modelu stają się takie same, co jest jednym z celów modelu.
Reszty (znane również jako terminy błędu) powinny być niezależne. Oznacza to, że nie ma korelacji między resztami a przewidywanymi wartościami lub między samymi resztami. Jeśli występuje jakaś korelacja, oznacza to, że istnieje zależność, której model regresji nie jest w stanie zidentyfikować. - Jeżeli zmienne niezależne nie są od siebie liniowo niezależne, traci się unikalność rozwiązania metodą najmniejszych kwadratów (lub rozwiązania równania normalnego).
Dołącz do kursu Sztucznej Inteligencji online z najlepszych światowych uniwersytetów – Masters, Executive Post Graduate Programs oraz Advanced Certificate Program in ML & AI, aby przyspieszyć swoją karierę.
3. Co to jest inżynieria funkcji? Jak to zastosować w procesie modelowania?
Inżynieria funkcji to proces przekształcania surowych danych w funkcje, które lepiej reprezentują problem leżący u podstaw modeli predykcyjnych
, co skutkuje poprawą dokładności modelu na niewidocznych danych.
W kategoriach laika inżynieria funkcji oznacza opracowywanie nowych funkcji, które mogą pomóc w lepszym zrozumieniu i modelowaniu problemu. Inżynieria funkcji jest dwojakiego rodzaju — oparta na biznesie i oparta na danych. Inżynieria funkcji oparta na biznesie obraca się wokół włączania funkcji z biznesowego punktu widzenia. Zadanie polega na przekształceniu zmiennych biznesowych w cechy problemu. W przypadku inżynierii funkcji opartej na danych, dodane funkcje nie mają żadnej znaczącej interpretacji fizycznej, ale pomagają modelowi w przewidywaniu zmiennej docelowej.
FYI: Darmowy kurs nlp!
Aby zastosować inżynierię cech, należy w pełni zapoznać się ze zbiorem danych. Wiąże się to z wiedzą o tym, jakie są dane dane, co oznaczają, jakie są surowe cechy itp. Musisz również mieć krystalicznie jasne pojęcie problemu, na przykład, jakie czynniki wpływają na zmienną docelową, jaka jest fizyczna interpretacja zmiennej itp.
4. Jaki jest pożytek z regularyzacji? Wyjaśnij regularyzacje L1 i L2.
Regularyzacja to technika, która służy do rozwiązania problemu nadmiernego dopasowania modelu. Kiedy bardzo złożony model jest zaimplementowany na danych uczących, przesadza. Czasami prosty model może nie być w stanie uogólnić danych, a złożony model przesunie się. Aby rozwiązać ten problem, stosuje się regularyzację.
Uregulowanie to nic innego jak dodanie warunków współczynnika (beta) do funkcji kosztu, tak aby warunki były karane i miały małą wartość. Zasadniczo pomaga to w uchwyceniu trendów w danych, a jednocześnie zapobiega nadmiernemu dopasowaniu, nie pozwalając, aby model stał się zbyt złożony.
- Regularyzacja L1 lub LASSO: Tutaj wartości bezwzględne współczynników są dodawane do funkcji kosztu. Widać to w poniższym równaniu; podświetlona część odpowiada regularyzacji L1 lub LASSO. Ta technika regularyzacji daje rzadkie wyniki, które również prowadzą do wyboru cech.
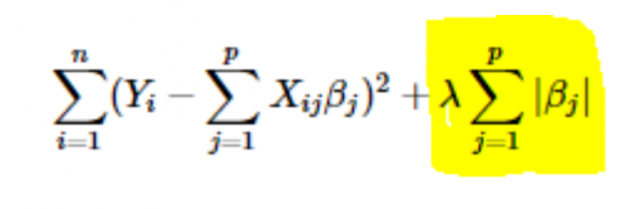
- Regularyzacja L2 lub Ridge: Tutaj kwadraty współczynników są dodawane do funkcji kosztu. Można to zobaczyć w poniższym równaniu, gdzie podświetlona część odpowiada regularyzacji L2 lub Ridge.
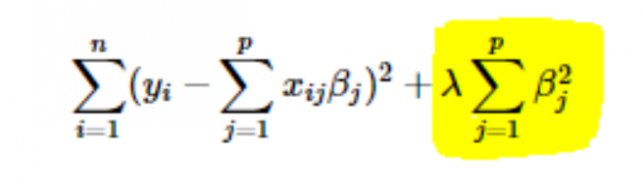
5. Jak wybrać wartość współczynnika uczenia się parametru (α)?
Wybór wartości współczynnika uczenia się to trudna sprawa. Jeśli wartość jest zbyt mała, algorytm zniżania gradientu potrzebuje wieków, aby uzyskać zbieżność do optymalnego rozwiązania. Z drugiej strony, jeśli wartość szybkości uczenia się jest wysoka, opadanie gradientu przekroczy optymalne rozwiązanie i najprawdopodobniej nigdy nie zbiegnie się do optymalnego rozwiązania.
Aby rozwiązać ten problem, możesz wypróbować różne wartości alfa w zakresie wartości i wykreślić koszt w zależności od liczby iteracji. Następnie na podstawie wykresów można wybrać wartość odpowiadającą wykresowi pokazującemu gwałtowny spadek. 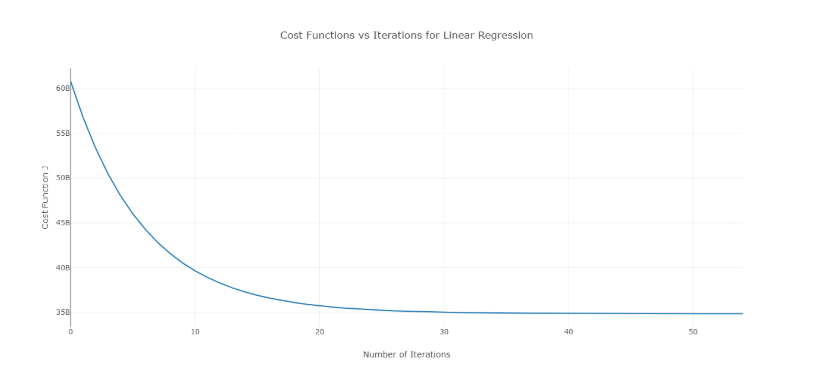
Wspomniany wykres to idealna krzywa kosztu w stosunku do liczby iteracji. Należy zauważyć, że początkowo koszt maleje wraz ze wzrostem liczby iteracji, ale po pewnych iteracjach opadanie gradientu jest zbieżne i koszt już się nie zmniejsza.
Jeśli widzisz, że koszt rośnie wraz z liczbą iteracji, twój parametr szybkości uczenia się jest wysoki i należy go zmniejszyć.
6. Jak wybrać wartość parametru regularyzacji (λ)?
Wybór parametru regularyzacji to trudna sprawa. Jeśli wartość λ będzie zbyt wysoka, doprowadzi to do skrajnie małych wartości współczynnika regresji β , co doprowadzi do niedopasowania modelu (high bias – niska wariancja). Z drugiej strony, jeśli wartość λ wynosi 0 (bardzo mała), model będzie miał tendencję do nadmiernego dopasowania danych uczących (niski błąd – duża wariancja).
Nie ma właściwego sposobu doboru wartości λ . To, co możesz zrobić, to mieć podpróbkę danych i wielokrotnie uruchamiać algorytm na różnych zestawach. Tutaj osoba musi zdecydować, ile wariancji może tolerować. Gdy użytkownik jest zadowolony z wariancji, tę wartość λ można wybrać dla pełnego zbioru danych.
Należy zauważyć, że wybrana tutaj wartość λ była optymalna dla tego podzbioru, a nie dla wszystkich danych treningowych.
7. Czy możemy wykorzystać regresję liniową do analizy szeregów czasowych?
Do analizy szeregów czasowych można zastosować regresję liniową, ale wyniki nie są obiecujące. Tak więc generalnie nie jest to zalecane. Powody tego są następujące:
- Dane szeregów czasowych są najczęściej używane do przewidywania przyszłości, ale regresja liniowa rzadko daje dobre wyniki dla przewidywania przyszłości, ponieważ nie jest przeznaczona do ekstrapolacji.
- Przeważnie dane szeregów czasowych mają wzór, taki jak w godzinach szczytu, sezonach świątecznych itp., który najprawdopodobniej zostanie potraktowany jako wartości odstające w analizie regresji liniowej.
8. Jakiej wartości jest suma reszt regresji liniowej bliska? Uzasadniać.
Odp . Suma reszt regresji liniowej wynosi 0. Regresja liniowa działa przy założeniu, że błędy (reszty) mają rozkład normalny ze średnią 0, tj.
Y = β T X + ε
Tutaj Y jest zmienną docelową lub zależną,
β jest wektorem współczynnika regresji,
X to macierz cech zawierająca wszystkie cechy jako kolumny,
ε jest wyrazem resztkowym takim, że ε ~ N(0,σ 2 ).
Tak więc suma wszystkich reszt to oczekiwana wartość reszt pomnożona przez całkowitą liczbę punktów danych. Ponieważ oczekiwanie reszt wynosi 0, suma wszystkich składników resztowych wynosi zero.
Uwaga : N(μ,σ 2 ) jest standardowym zapisem rozkładu normalnego o średniej μ i odchyleniu standardowym σ 2 .
9. Jak wielokoliniowość wpływa na regresję liniową?
Ans Multicollinearity występuje, gdy niektóre zmienne niezależne są ze sobą silnie skorelowane (dodatnie lub ujemnie). Ta wielowspółliniowość stwarza problem, ponieważ jest sprzeczna z podstawowym założeniem regresji liniowej. Obecność wielokoliniowości nie wpływa na zdolność predykcyjną modelu. Tak więc, jeśli chcesz tylko przewidywać, obecność współliniowości nie wpływa na wyniki. Jeśli jednak chcesz wyciągnąć pewne spostrzeżenia z modelu i zastosować je, powiedzmy, w jakimś modelu biznesowym, może to spowodować problemy.
Jednym z głównych problemów powodowanych przez współliniowość jest to, że prowadzi ona do błędnych interpretacji i dostarcza błędnych spostrzeżeń. Współczynniki regresji liniowej sugerują średnią zmianę wartości docelowej w przypadku zmiany cechy o jedną jednostkę. Tak więc, jeśli istnieje wielowspółliniowość, nie jest to prawdą, ponieważ zmiana jednej cechy doprowadzi do zmian w skorelowanej zmiennej iw konsekwencji do zmian w zmiennej docelowej. Prowadzi to do błędnych spostrzeżeń i może przynieść niebezpieczne wyniki dla firmy.
Bardzo skutecznym sposobem radzenia sobie z wielokoliniowością jest zastosowanie współczynnika VIF (Variance Inflation Factor). Wyższa wartość VIF dla cechy, bardziej liniowo skorelowana jest ta cecha. Po prostu usuń funkcję o bardzo wysokiej wartości VIF i ponownie przeszkol model na pozostałym zbiorze danych.
10. Jaka jest postać normalna (równanie) regresji liniowej? Kiedy należy go preferować od metody zejścia gradientowego?
Normalne równanie regresji liniowej to —
β=( XTX ) -1 . X T Y
Tutaj Y=β T X jest modelem regresji liniowej,
Y jest zmienną docelową lub zależną,
β jest wektorem współczynnika regresji, który uzyskuje się za pomocą równania normalnego,
X to macierz cech zawierająca wszystkie cechy jako kolumny.
Zauważ, że pierwsza kolumna w macierzy X składa się z samych jedynek. Ma to na celu uwzględnienie wartości przesunięcia dla linii regresji.
Porównanie między spadkiem gradientowym a równaniem normalnym:
| Zejście gradientowe | Równanie normalne |
| Wymaga strojenia hiperparametrów dla alfa (parametr uczenia) | Nie ma takiej potrzeby |
| Jest to proces iteracyjny | Jest to proces nieiteracyjny |
| O(kn 2 ) złożoność czasowa | O(n 3 ) złożoność czasowa wynikająca z oceny X T X |
| Preferowane, gdy n jest bardzo duże | Staje się dość powolny dla dużych wartości n |
Tutaj ' k ' to maksymalna liczba iteracji dla opadania gradientu, a ' n ' to całkowita liczba punktów danych w zbiorze uczącym.
Oczywiście, jeśli mamy duże dane treningowe, normalne równanie nie jest preferowane do użycia. Dla małych wartości ' n ' normalne równanie jest szybsze niż opadanie gradientowe.
Co to jest uczenie maszynowe i dlaczego ma to znaczenie
11. Przeprowadzasz regresję na różnych podzbiorach danych i w każdym podzbiorze wartość beta dla pewnej zmiennej jest bardzo zróżnicowana. Jaki może być tutaj problem?
Ten przypadek sugeruje, że zbiór danych jest niejednorodny. Aby rozwiązać ten problem, zestaw danych powinien być pogrupowany w różne podzbiory, a następnie dla każdego klastra należy zbudować oddzielne modele. Innym sposobem radzenia sobie z tym problemem jest wykorzystanie modeli nieparametrycznych, takich jak drzewa decyzyjne, które dość skutecznie radzą sobie z heterogenicznymi danymi.

12. Twoja regresja liniowa nie działa i komunikuje, że istnieje nieskończona liczba najlepszych szacunków dla współczynników regresji. Co może być nie tak?
Warunek ten powstaje, gdy między niektórymi zmiennymi istnieje doskonała korelacja (dodatnia lub ujemna). W tym przypadku nie ma jednoznacznej wartości współczynników, a co za tym idzie, powstaje dany warunek.
13. Co rozumiesz przez skorygowane R 2 ? Czym różni się od R 2 ?
Skorygowane R 2 , podobnie jak R 2 , jest reprezentantem liczby punktów leżących wokół linii regresji. Oznacza to, że pokazuje, jak dobrze model pasuje do danych uczących. Wzór na skorygowany R 2 jest -
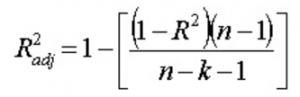
Tutaj n to liczba punktów danych, a k to liczba cech.
Jedna wada R 2 jest to, że zawsze będzie się zwiększać wraz z dodaniem nowej funkcji, niezależnie od tego, czy nowa funkcja jest przydatna, czy nie. Skorygowany R 2 przezwycięża tę wadę. Wartość skorygowanego R 2 wzrasta tylko wtedy, gdy nowo dodana funkcja odgrywa znaczącą rolę w modelu.
14. Jak interpretujesz krzywą wartości rezydualnej i dopasowanej?
Wykres wartości rezydualnej i dopasowanej służy do sprawdzenia, czy wartości przewidywane i reszty mają korelację, czy nie. Jeśli reszty mają rozkład normalny, ze średnią wokół dopasowanej wartości i stałą wariancją, nasz model działa dobrze; w przeciwnym razie jest jakiś problem z modelem.
Najczęstszym problemem, który można znaleźć podczas uczenia modelu w dużym zakresie zbioru danych, jest heteroskedastyczność (wyjaśniono to w odpowiedzi poniżej). Obecność heteroskedastyczności można łatwo zauważyć, wykreślając krzywą wartości rezydualnej w funkcji dopasowanej wartości.
15. Co to jest heteroskedastyczność? Jakie są konsekwencje i jak możesz je przezwyciężyć?
Mówi się, że zmienna losowa jest heteroskedastyczna, gdy różne subpopulacje mają różne zmienności (odchylenie standardowe).
Istnienie heteroskedastyczności rodzi pewne problemy w analizie regresji, ponieważ założenie mówi, że terminy błędu są nieskorelowane, a zatem wariancja jest stała. Obecność heteroskedastyczności często można zaobserwować w postaci stożkowego wykresu rozrzutu dla wartości resztowych względem dopasowanych.
Jednym z podstawowych założeń regresji liniowej jest brak heteroskedastyczności w danych. Ze względu na naruszenie założeń estymatory zwykłych najmniejszych kwadratów (OLS) nie są najlepszymi liniowymi estymatorami nieobciążonymi (BLUE). W związku z tym nie dają najmniejszej wariancji niż inne liniowe nieobciążone estymatory (LUE).
Nie ma ustalonej procedury przezwyciężenia heteroskedastyczności. Istnieje jednak kilka sposobów, które mogą prowadzić do zmniejszenia heteroskedastyczności. Oni są -
- Logarytmowanie danych: szereg, który rośnie wykładniczo, często skutkuje zwiększoną zmiennością. Można to przezwyciężyć za pomocą transformacji dziennika.
- Korzystanie z ważonej regresji liniowej: W tym przypadku metoda OLS jest stosowana do ważonych wartości X i Y. Jednym ze sposobów jest przypisanie wag bezpośrednio związanych z wielkością zmiennej zależnej.
16. Co to jest VIF? Jak to obliczyć?
Współczynnik inflacji wariancji (VIF) służy do sprawdzania obecności wielokoliniowości w zbiorze danych. Jest obliczany jako:
Tutaj VIF j jest wartością VIF dla j- tej zmiennej,
Rj 2 jest wartością R 2 modelu, gdy ta zmienna jest regresowana względem wszystkich innych zmiennych niezależnych.
Jeśli wartość VIF jest wysoka dla zmiennej, oznacza to, że R 2 wartość odpowiedniego modelu jest wysoka, tzn. inne zmienne niezależne są w stanie wyjaśnić tę zmienną. Mówiąc prościej, zmienna jest liniowo zależna od kilku innych zmiennych.
17. Skąd wiesz, że regresja liniowa jest odpowiednia dla dowolnych danych?
Aby sprawdzić, czy regresja liniowa jest odpowiednia dla dowolnych danych, można użyć wykresu punktowego. Jeśli zależność wygląda liniowo, możemy wybrać model liniowy. Ale jeśli tak nie jest, musimy zastosować pewne przekształcenia, aby zależność była liniowa. Wykreślanie wykresów punktowych jest łatwe w przypadku prostej lub jednowymiarowej regresji liniowej. Jednak w przypadku wielowymiarowej regresji liniowej można wykreślić dwuwymiarowe wykresy rozrzutu parami, wykresy obrotowe i wykresy dynamiczne.
18. W jaki sposób testowanie hipotez jest wykorzystywane w regresji liniowej?
Testowanie hipotez można przeprowadzić w regresji liniowej w następujących celach:
- Aby sprawdzić, czy predyktor jest istotny dla predykcji zmiennej docelowej. Dwie popularne metody to —
- Za pomocą wartości p:
Jeżeli wartość p zmiennej jest większa niż pewna granica (zwykle 0,05), zmienna jest nieistotna w przewidywaniu zmiennej docelowej. - Sprawdzając wartości współczynnika regresji:
Jeżeli wartość współczynnika regresji odpowiadającego predyktorowi wynosi zero, zmienna ta jest nieistotna w przewidywaniu zmiennej docelowej i nie ma z nią liniowej zależności.
- Za pomocą wartości p:
- Aby sprawdzić, czy obliczone współczynniki regresji są dobrymi estymatorami rzeczywistych współczynników.
19. Wyjaśnij opadanie gradientowe w odniesieniu do regresji liniowej.
Zejście gradientowe to algorytm optymalizacji. W regresji liniowej służy do optymalizacji funkcji kosztu i znalezienia wartości βs (estymatorów) odpowiadających zoptymalizowanej wartości funkcji kosztu.
Opadanie gradientowe działa jak kula tocząca się po wykresie (ignorując bezwładność). Kula porusza się w kierunku największego nachylenia i zatrzymuje się na płaskiej powierzchni (minima). 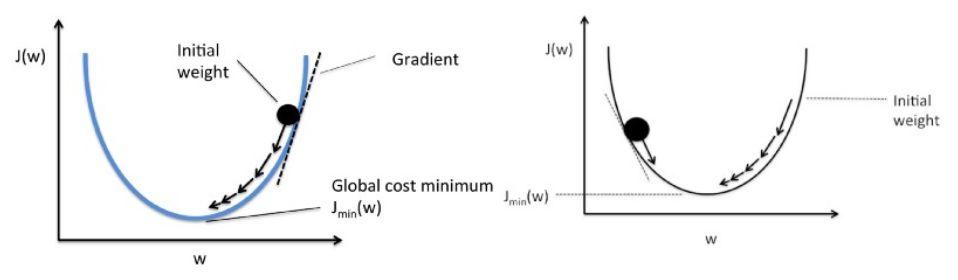
Matematycznie celem opadania gradientu dla regresji liniowej jest znalezienie rozwiązania
ArgMin J(Θ 0 ,Θ 1 ), gdzie J(Θ 0 ,Θ 1 ) jest funkcją kosztu regresji liniowej. Daje to — 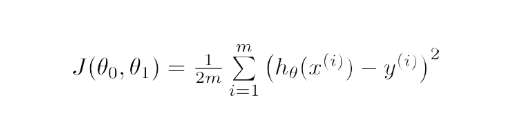
Tutaj h jest liniowym modelem hipotezy, h=Θ 0 + Θ 1 x, y to prawdziwe wyjście, a m to liczba punktów danych w zbiorze uczącym.
Gradient Descent rozpoczyna się od losowego rozwiązania, a następnie na podstawie kierunku gradientu rozwiązanie jest aktualizowane do nowej wartości, gdy funkcja kosztu ma niższą wartość.
Aktualizacja to:
Powtarzaj aż do zbieżności 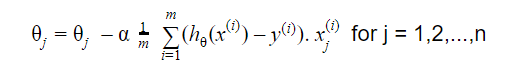
20. Jak interpretujesz model regresji liniowej?
Model regresji liniowej jest dość łatwy do interpretacji. Model ma następującą postać: 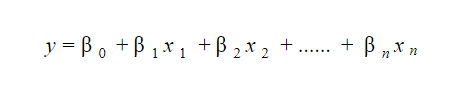
Znaczenie tego modelu polega na tym, że można łatwo zinterpretować i zrozumieć marginalne zmiany i ich konsekwencje. Na przykład, jeśli wartość x 0 wzrośnie o 1 jednostkę, utrzymując inne zmienne na stałym poziomie, całkowity wzrost wartości y wyniesie β i . Matematycznie termin przecięcia ( β 0 ) jest odpowiedzią, gdy wszystkie predyktory są ustawione na zero lub nie są brane pod uwagę.
Te 6 technik uczenia maszynowego usprawnia opiekę zdrowotną
21. Co to jest solidna regresja?
Model regresji powinien mieć solidny charakter. Oznacza to, że przy zmianach kilku obserwacji model nie powinien zmieniać się drastycznie. Ponadto wartości odstające nie powinny mieć na nią większego wpływu.
Model regresji z OLS (zwykłymi najmniejszymi kwadratami) jest dość wrażliwy na wartości odstające. Aby rozwiązać ten problem, możemy użyć metody WLS (Weighted Least Squares) do wyznaczenia estymatorów współczynników regresji. W tym przypadku wartościom odstającym lub punktom o wysokiej dźwigni w okuciu przypisuje się mniejszą wagę, co sprawia, że punkty te mają mniejszy wpływ.
22. Które wykresy sugeruje się obserwować przed dopasowaniem modelu?
Przed dopasowaniem modelu należy dobrze poznać dane, takie jak trendy, rozkład, skośność itp. w zmiennych. Wykresy, takie jak histogramy, wykresy pudełkowe i wykresy punktowe, można wykorzystać do obserwacji rozkładu zmiennych. Poza tym należy również przeanalizować, jaki jest związek między zmiennymi zależnymi i niezależnymi. Można to zrobić za pomocą wykresów punktowych (w przypadku problemów jednowymiarowych), wykresów obrotowych, wykresów dynamicznych itp.
23. Czym jest uogólniony model liniowy?
Uogólniony model liniowy jest pochodną zwykłego modelu regresji liniowej. GLM jest bardziej elastyczny pod względem reszt i może być stosowany tam, gdzie regresja liniowa nie wydaje się odpowiednia. GLM pozwala, aby rozkład reszt był inny niż rozkład normalny. Uogólnia regresję liniową, umożliwiając połączenie modelu liniowego ze zmienną docelową za pomocą funkcji łączenia. Estymacja modelu odbywa się metodą największej wiarygodności.
24. Wyjaśnij kompromis między stronniczością a wariancją.
Bias odnosi się do różnicy między wartościami przewidywanymi przez model a wartościami rzeczywistymi. To jest błąd. Jednym z celów algorytmu ML jest niska stronniczość.
Wariancja odnosi się do wrażliwości modelu na małe wahania w uczącym zbiorze danych. Innym celem algorytmu ML jest niska wariancja.
W przypadku zbioru danych, który nie jest dokładnie liniowy, nie jest możliwe jednoczesne uzyskanie zarówno niskiego obciążenia, jak i wariancji. Model linii prostej będzie miał niską wariancję, ale wysoką wariancję, podczas gdy wielomian wysokiego stopnia będzie miał małą wariancję, ale wysoką wariancję.
Nie da się uniknąć związku między stronniczością a wariancją w uczeniu maszynowym.
- Zmniejszenie odchylenia zwiększa wariancję.
- Zmniejszenie wariancji zwiększa błąd systematyczny.
Tak więc istnieje kompromis między tymi dwoma; specjalista od ML musi zdecydować, w oparciu o przydzielony problem, ile stronniczości i wariancji może być tolerowane. Na tej podstawie budowany jest ostateczny model.
25. W jaki sposób krzywe uczenia się mogą pomóc w stworzeniu lepszego modelu?
Krzywe uczenia się wskazują na obecność nadmiernego lub niedostatecznego dopasowania.
Na krzywej uczenia się błąd uczący i błąd walidacji krzyżowej są wykreślane w funkcji liczby uczących punktów danych. Typowa krzywa uczenia się wygląda tak: 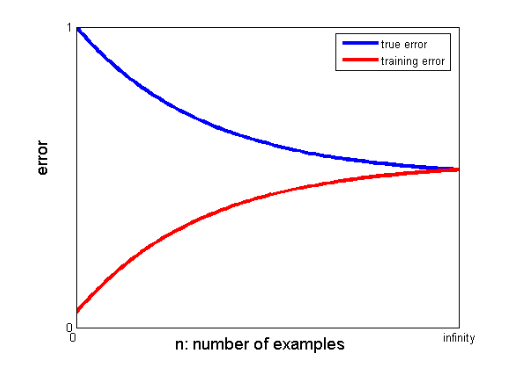
Jeśli błąd uczący i błąd prawdziwy (błąd walidacji krzyżowej) zbiegają się do tej samej wartości, a odpowiadająca jej wartość błędu jest wysoka, oznacza to, że model jest niedopasowany i ma duże obciążenie.
Wywiady o uczeniu maszynowym i jak je zaliczyć
Wywiady na temat uczenia maszynowego mogą się różnić w zależności od rodzaju lub kategorii, na przykład kilku rekruterów zadaje wiele pytań do rozmowy kwalifikacyjnej z użyciem regresji liniowej . Wybierając się do roli inżyniera uczenia maszynowego, mogą specjalizować się w kategoriach takich jak kodowanie, badania, studium przypadku, zarządzanie projektami, prezentacja, projektowanie systemu i statystyka. Skoncentrujemy się na najczęstszych typach kategorii i sposobach przygotowania się do nich.
- Kodowanie
Kodowanie i programowanie są ważnymi elementami rozmowy kwalifikacyjnej dotyczącej uczenia maszynowego i są często wykorzystywane do sprawdzania kandydatów. Aby dobrze wypaść w tych rozmowach, musisz mieć solidne umiejętności programistyczne. Wywiady dotyczące kodowania zwykle trwają od 45 do 60 minut i składają się tylko z dwóch pytań. Ankieter stawia temat i przewiduje, że wnioskodawca zajmie się nim w jak najkrótszym czasie.
Jak się przygotować – Możesz przygotować się do tych rozmów, dobrze rozumiejąc struktury danych, złożoność czasu i przestrzeni, umiejętności zarządzania oraz umiejętność zrozumienia i rozwiązania problemu. upGrad ma świetny kurs inżynierii oprogramowania, który może pomóc Ci poprawić umiejętności kodowania i pomóc w przeprowadzeniu rozmowy kwalifikacyjnej.
2. Uczenie maszynowe
Twoje zrozumienie uczenia maszynowego zostanie ocenione podczas rozmów kwalifikacyjnych. Warstwy konwolucyjne, rekurencyjne sieci neuronowe, generatywne sieci przeciwników, rozpoznawanie mowy i inne tematy mogą być omawiane w zależności od potrzeb związanych z zatrudnieniem.
Jak się przygotować – Aby móc podołać tej rozmowie kwalifikacyjnej, musisz upewnić się, że dokładnie rozumiesz role i obowiązki w pracy. Pomoże Ci to zidentyfikować specyfikacje ML, które musisz przestudiować. Jeśli jednak nie natkniesz się na żadne specyfikacje, musisz dogłębnie zrozumieć podstawy. Pomoże Ci w tym dogłębny kurs ML, który zapewnia upGrad. Możesz także zapoznać się z najnowszymi artykułami na temat uczenia maszynowego i sztucznej inteligencji, aby zrozumieć ich najnowsze trendy i regularnie je uwzględniać.
3. Badania przesiewowe
Ten wywiad jest nieco nieformalny i zazwyczaj jest jednym z początkowych punktów rozmowy. Często zajmuje się tym potencjalny pracodawca. Głównym celem tej rozmowy jest przedstawienie kandydatowi poczucia biznesu, roli i obowiązków. W bardziej nieformalnej atmosferze kandydat jest również pytany o jego przeszłość, aby ustalić, czy jego obszar zainteresowań odpowiada stanowisku.
Jak się przygotować – To bardzo nietechniczna część rozmowy. Wszystko, czego potrzebujesz, to Twoja uczciwość i podstawy Twojej specjalizacji w uczeniu maszynowym.
4. Projekt systemu
Takie wywiady sprawdzają zdolność danej osoby do stworzenia w pełni skalowalnego rozwiązania od początku do końca. Większość inżynierów jest tak zajęta problemem, że często pomija szerszy obraz. Wywiad dotyczący projektu systemu wymaga zrozumienia wielu elementów, które składają się na rozwiązanie. Te elementy obejmują układ frontonu, system równoważenia obciążenia, pamięć podręczną i inne. Skuteczny i skalowalny system end-to-end jest łatwiejszy do opracowania, gdy te kwestie są dobrze zrozumiane.
Jak się przygotować – Zrozum koncepcje i elementy projektu projektowania systemu. Użyj przykładów z życia, aby wyjaśnić strukturę ankieterowi, aby lepiej zrozumieć projekt.
Popularne blogi dotyczące uczenia maszynowego i sztucznej inteligencji
| IoT: historia, teraźniejszość i przyszłość | Samouczek uczenia maszynowego: Naucz się ML | Co to jest algorytm? Proste i łatwe |
| Wynagrodzenie inżyniera robotyki w Indiach: wszystkie role | Dzień z życia inżyniera uczenia maszynowego: czym się zajmują? | Czym jest IoT (Internet Rzeczy) |
| Permutacja a kombinacja: różnica między permutacją a kombinacją | 7 najważniejszych trendów w sztucznej inteligencji i uczeniu maszynowym | Uczenie maszynowe z R: wszystko, co musisz wiedzieć |

Jeżeli istnieje znaczna luka między zbieżnymi wartościami uczącymi a błędami walidacji krzyżowej, tj. błąd walidacji krzyżowej jest znacznie wyższy od błędu uczącego, sugeruje to, że model jest zbyt dopasowany do danych uczących i wykazuje dużą wariancję .
Inżynierowie uczenia maszynowego: mity a rzeczywistość
To koniec pierwszej części tej serii. Pozostań przy kolejnej części serii, która składa się z pytań opartych na regresji logistycznej . Zapraszam do publikowania komentarzy.
Współautor – Ojas Agarwal
Możesz sprawdzić nasz program Executive PG w zakresie uczenia maszynowego i sztucznej inteligencji , który zapewnia praktyczne warsztaty praktyczne, mentor branżowy jeden na jednego, 12 studiów przypadków i zadań, status absolwentów IIIT-B i nie tylko.
Co rozumiesz przez regularyzację?
Regularyzacja to strategia radzenia sobie z problemem nadmiernego dopasowania modelu. Overfitting występuje, gdy do danych uczących stosuje się skomplikowany model. Podstawowy model może czasami nie być w stanie uogólnić danych, a skomplikowany model może przepełnić dane. Regularyzacja służy do złagodzenia tego problemu. Regularyzacja to proces dodawania terminów współczynników (beta) do problemu minimalizacji w taki sposób, że terminy są karane i mają skromną wielkość. Zasadniczo pomaga to w identyfikacji wzorców danych, jednocześnie zapobiegając nadmiernemu dopasowaniu, zapobiegając zbytniej złożoności modelu.
Co rozumiesz o inżynierii funkcji?
Proces zamiany oryginalnych danych na cechy, które lepiej opisują podstawowy problem modeli predykcyjnych, co skutkuje zwiększoną dokładnością modelu na niewidocznych danych, jest znany jako inżynieria cech. W kategoriach laika inżynieria funkcji odnosi się do tworzenia dodatkowych funkcji, które mogą pomóc w lepszym zrozumieniu i modelowaniu problemu. Istnieją dwa rodzaje inżynierii funkcji: opartą na biznesie i opartą na danych. Włączenie funkcji z komercyjnego punktu widzenia jest głównym celem inżynierii funkcji zorientowanej na biznes.
Jaki jest kompromis między stronniczością a wariancją?
Luka pomiędzy modelem - wartościami przewidywanymi a wartościami rzeczywistymi nazywana jest biasem. To pomyłka. Niskie obciążenie jest jednym z celów algorytmu ML. Podatność modelu na drobne zmiany w uczącym zbiorze danych jest określana jako wariancja. Niska wariancja to kolejny cel algorytmu ML. Niemożliwe jest posiadanie zarówno niskiego błędu systematycznego, jak i małej wariancji w zbiorze danych, który nie jest idealnie liniowy. Wariancja modelu liniowego jest niska, ale obciążenie jest duże, podczas gdy wariancja wielomianu wysokiego stopnia jest niska, ale obciążenie jest wysokie. W uczeniu maszynowym związek między uprzedzeniami a zmiennością jest nieunikniony.
