Wprowadzenie do funkcji gęstości prawdopodobieństwa [wzór, właściwości, zastosowania, przykłady]

Funkcja gęstości prawdopodobieństwa (PDF) to wyrażenie w statystyce, które oznacza rozkład prawdopodobieństwa dyskretnej zmiennej losowej. Rozkład prawdopodobieństwa, w uproszczeniu, można zdefiniować jako prawdopodobieństwo wyniku zmiennej losowej, takiej jak akcje lub ETF. Zmienne dyskretne występują w przeciwieństwie do ciągłej zmiennej losowej, której dokładną wartość można określić.

Na przykład wartość scrip na giełdzie ma tylko dwa miejsca po przecinku (na przykład 65,76) w dyskretnej zmiennej losowej zamiast zmiennej ciągłej z dowolną liczbą miejsc po przecinku (przykład: 65.7685434567).

Funkcja gęstości prawdopodobieństwa jest narzędziem statystycznym używanym do określenia prawdopodobieństwa wyniku dyskretnej zmiennej losowej. Po wykreśleniu na wykresie pliki PDF wyglądają identycznie jak krzywa dzwonowa, w której obszar pod krzywą reprezentuje prawdopodobieństwo wyniku.

W przypadku rzutowania jako modelu graficznego obszar pod krzywą reprezentuje zakres, w którym spadną wartości dyskretnych zmiennych losowych. Zatem całkowita powierzchnia pod krzywą jest równa prawdopodobieństwu wyniku zmiennej.

Funkcja gęstości prawdopodobieństwa może określić prawdopodobieństwo, że zmienna losowa mieści się w określonym przedziale wartości.

Zazwyczaj funkcje gęstości prawdopodobieństwa analizują ryzyko i potencjalne przychody związane z określonym funduszem na rynku akcji.

Warunki, które musi spełnić funkcja, która ma być uważana za funkcję gęstości prawdopodobieństwa

Wartość zmiennej dyskretnej można dokładnie zmierzyć w przeciwieństwie do zmiennej ciągłej, która może mieć nieskończoną liczbę wartości. Każda funkcja powinna spełniać poniższe dwa warunki, aby być funkcją gęstości prawdopodobieństwa:

• Wartość f(x) dla każdej możliwej wartości zmiennej losowej powinna być dodatnia (nieujemna).
• Wartość całkowa całkowitego pola powierzchni krzywej (całka wszystkich możliwych wartości zmiennej losowej) powinna wynosić 1.

Różnica między funkcją gęstości prawdopodobieństwa a funkcją rozkładu prawdopodobieństwa

Zmienne losowe mogą mieć wiele wartości. Opis każdej możliwej wartości, jaką może mieć zmienna losowa, nazywa się jej rozkładem prawdopodobieństwa.

Rozkład prawdopodobieństwa daje zestaw wyników i związanych z nimi prawdopodobieństw. Funkcja statystyczna reprezentująca ciągły rozkład prawdopodobieństwa jest znana jako funkcja gęstości prawdopodobieństwa.

Istnieje inne narzędzie statystyczne, które reprezentuje dyskretny rozkład prawdopodobieństwa zwany funkcją masy prawdopodobieństwa. Daje to szczegółowy opis wszystkich możliwych wyników i ich prawdopodobieństw.

Wyrażenie funkcji gęstości prawdopodobieństwa

Jeśli zmienna losowa jest dyskretna, jej rozkład prawdopodobieństwa nazywa się funkcją masy prawdopodobieństwa, a jeśli jest zmienną ciągłą, rozkład prawdopodobieństwa nazywa się funkcją gęstości prawdopodobieństwa.

Plik PDF jest używany, gdy dana zmienna losowa ma zakres możliwych wartości. Ich rozkład prawdopodobieństwa służy do określenia dokładnej wartości.

Niech zmienna losowa będzie oznaczona przez X. Funkcja gęstości prawdopodobieństwa f zmiennej losowej X może być wyrażona jako

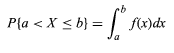
• Wartość zmiennej losowej mieści się między a i b.
• Jeżeli X oznacza prawdopodobieństwo wybrania określonej liczby z przedziału (przedziału) r i s, to funkcję gęstości prawdopodobieństwa można wyrazić jako

f ( x ) = 1/( s − r ) dla r < x < s i f ( x ) = 0 dla x < r lub x > s .

• PDF F jest reprezentowany jako:

F ( x ) = P { X ≤ x }

która jest nazywana dystrybuantą lub dystrybuantą X.

Biorąc pod uwagę, że zmienna losowa X ma rozkład prawdopodobieństwa f ( x ), to zależność między f i F można ustalić jako

F ′(. x ) = f ( x )

Funkcja dystrybucji dyskretnej zmiennej losowej różni się od jej funkcji rozkładu prawdopodobieństwa. Związek między nimi można wyrazić następująco:

Oczekiwanie zmiennej losowej jest oznaczone jako,

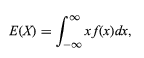
W ten sposób wszystkie zmienne dyskretne i losowe można traktować jednolicie za pomocą połączonej teorii.

Formuła funkcji gęstości prawdopodobieństwa

Prawdopodobieństwo wystąpienia ciągłej zmiennej losowej X na pewnej stałej wartości x jest zawsze równe 0. W tym przypadku nie można użyć P(X = x). Należy określić wartość X mieszczącą się w przedziale wartości (a,b). Aby to określić, stosuje się następujący wzór.

Właściwości funkcji gęstości prawdopodobieństwa

Ciągła zmienna losowa, która przyjmuje swoją wartość między zakresem (a, b), na przykład, zostanie oszacowana przez obliczenie obszaru pod krzywą i osią X wykreśloną z (a) jako jej dolną granicą i (b) jako jej Górna granica. Funkcja gęstości prawdopodobieństwa dla powyższego jest reprezentowana jako:

Funkcja gęstości prawdopodobieństwa jest dodatnia (nieujemna) dla wszystkich możliwych wartości. Oznacza to f(x)≥ 0, dla każdego x. Pole pomiędzy krzywą gęstości a osią X (oś poziomą) wynosi 1.

Można to również oznaczyć jako:

Krzywa funkcji gęstości jest ciągła w całym podanym zakresie, który jest wyraźnie zdefiniowany w odniesieniu do szeregu wartości ciągłych lub dziedziny zmiennej.

Dołącz do kursu uczenia maszynowego online z najlepszych uniwersytetów na świecie — studiów magisterskich, programów podyplomowych dla kadry kierowniczej i zaawansowanego programu certyfikacji w zakresie uczenia maszynowego i sztucznej inteligencji, aby przyspieszyć swoją karierę.

Zastosowania funkcji gęstości prawdopodobieństwa

• Funkcja gęstości prawdopodobieństwa jest wykorzystywana w rocznym modelowaniu poziomów stężenia NO w atmosferze.
• Modelowanie spalania silników Diesla.
• W statystyce funkcja gęstości prawdopodobieństwa służy do określenia możliwości wyniku zmiennej losowej.

Przykłady funkcji gęstości prawdopodobieństwa

• Przykład 1

Poniżej znajduje się przykład wykorzystania funkcji gęstości prawdopodobieństwa (PDF) do określenia potencjału ryzyka inwestora na giełdzie:

Po pierwsze, pliki PDF są generowane jako narzędzie graficzne na podstawie informacji historycznych.

Najpopularniejszą formą PDF jest projekcja neutralna, w której ryzyko jest równe nagrodzie w wielu różnych możliwościach. Inwestorzy o mniejszej zdolności do podejmowania ryzyka zostaną nagrodzeni jedynie ograniczonymi zyskami, a zatem znajdą się pod lewą stroną krzywej dzwonowej. Z drugiej strony, inwestorzy o dużych zdolnościach do podejmowania ryzyka prawdopodobnie zostaną nagrodzeni wyższymi zyskami, a zatem spadną pod prawą stronę krzywej.

Większość inwestorów ma przeciętną zdolność do podejmowania ryzyka i dlatego zajmują środek krzywej.

Pomaga to w analizie kategorii inwestorów na podstawie otrzymanych danych. Pomaga to brokerom giełdowym w identyfikacji docelowej kategorii klientów do sprzedaży ich produktów.

• Przykład 2

Jednym z podstawowych zastosowań funkcji gęstości prawdopodobieństwa jest zmienna losowa Gaussa, znana również jako normalna zmienna losowa.

W obu przypadkach wykres przedstawia krzywą dzwonową dla funkcji gęstości prawdopodobieństwa.

Gęstość można wyrazić jako

Wykres powyższego równania gęstości podano poniżej.

Obszar pod krzywą reprezentuje rzeczywistą wartość zmiennej losowej Gaussa.

Wniosek

Funkcja gęstości prawdopodobieństwa odgrywa istotną rolę w uczeniu maszynowym. Uczniom, którzy chcą rozpocząć karierę w dziedzinie uczenia maszynowego i sztucznej inteligencji, zdecydowanie zalecamy zapisanie się do programu certyfikatów zaawansowanych IIT w zakresie uczenia maszynowego . Program jest dostosowany i zaprojektowany, aby wyposażyć starszych profesjonalistów do wdrażania modeli uczenia maszynowego z wykorzystaniem technologii przetwarzania w chmurze.

Program nauczania został opracowany przez wykładowców IIT Madras i ekspertów branżowych, aby proces uczenia się był bardziej odpowiedni i praktyczny. Program oferuje uznawany na całym świecie certyfikat prestiżowej i zajmującej pierwsze miejsce w rankingu uczelni inżynierskiej w Indiach oraz 360-stopniowe wsparcie w zakresie stażu od upGrad.

Co więcej, otrzymujesz liczne możliwości współpracy przy dużych projektach z bazą płatnych uczniów upGrad liczącą ponad 40 000 osób.

Wejdź na naszą stronę internetową, aby rozpocząć swoją podróż edukacyjną!