Wprowadzenie do regresji wielowymiarowej w uczeniu maszynowym: kompletny przewodnik

Nie jest tajemnicą, że dzisiejsza technologia opiera się na danych. Dane mogą być jedynie kompilacją danych liczbowych, ale można je przetwarzać w sposób znaczący, aby wydobyć produktywność i zaradność, aby firmy pozostały konkurencyjne i zrównoważone w dłuższej perspektywie. Tak się składa, że ​​analiza danych jest odpowiedzią na wyprowadzenie dokładnych szacunków z surowych informacji.

Analiza danych to technika, która wykorzystuje pomysły statystyczne i logiczne do analizy, przetwarzania i przekształcania danych w użyteczną formę. Rozwiązania wynikające z analizy danych są wykorzystywane w biznesie do podejmowania ważnych decyzji. Nauka o danych wraz z analizą danych służy do przewidywania przyszłych wyników z dużą dokładnością. Jest to proces polegający na wykorzystaniu technik naukowych i algorytmów w celu uzyskania realnych informacji z puli danych.

Częstym problemem, z którym borykają się specjaliści ds. danych, jest sposób, w jaki można określić, czy istnieje statystyczny związek między zmienną odpowiedzi (oznaczoną przez Y) a zmiennymi objaśniającymi (oznaczonymi przez Xi).

Odpowiedzią na ten problem jest analiza regresji. Rozumiemy to bardziej szczegółowo.

Co to jest analiza regresji?

Analiza regresji jest jedną z popularnych metod analizy danych, która wykorzystuje kontrolowany lub nadzorowany algorytm uczenia maszynowego. Jest to skuteczna technika identyfikacji i ustalenia relacji między zmiennymi w danych.

Analiza regresji polega na sortowaniu opłacalnych zmiennych za pomocą strategii matematycznych w celu wyciągnięcia bardzo dokładnych wniosków na temat tych posortowanych zmiennych.

Co to jest regresja wielowymiarowa?

Wiele zmiennych to kontrolowany lub nadzorowany algorytm uczenia maszynowego, który analizuje wiele zmiennych danych. Jest to kontynuacja regresji wielokrotnej, która obejmuje jedną zmienną zależną i wiele zmiennych niezależnych. Wynik jest przewidywany na podstawie liczby zmiennych niezależnych.

Regresja wielowymiarowa tworzy wzór, który wyjaśnia jednoczesną reakcję czynników obecnych w zmiennych na zmiany w innych. Służą do badania danych z różnych dziedzin. Na przykład w nieruchomościach regresja wielowymiarowa służy do przewidywania ceny domu na podstawie kilku czynników, takich jak jego lokalizacja, liczba pokoi i dostępne udogodnienia.

Funkcja kosztu w regresji wielowymiarowej

Funkcja kosztu przypisuje koszt do próbek, gdy wynik modelu odbiega od zaobserwowanych danych. Równanie funkcji kosztu to suma kwadratu różnicy między wartością przewidywaną a wartością rzeczywistą podzieloną przez dwukrotność długości zbioru danych.

Oto przykład :

Wynik :

Źródło

Jak korzystać z analizy regresji wielowymiarowej?

Procesy zaangażowane w wielowymiarową analizę regresji obejmują wybór cech, inżynierię cech, normalizację cech, funkcje utraty selekcji, analizę hipotez i tworzenie modelu regresji.

1. Wybór cech: Jest to najważniejszy krok w regresji wielowymiarowej. Proces ten, znany również jako selekcja zmiennych, obejmuje wybór opłacalnych zmiennych w celu zbudowania wydajnych modeli.
2. Normalizacja funkcji: Obejmuje skalowanie funkcji w celu utrzymania usprawnionej dystrybucji i współczynników danych. Pomaga to w lepszej analizie danych. Wartość wszystkich funkcji można zmienić zgodnie z wymaganiami.
3. Wybór funkcji straty i hipotezy : Funkcja straty służy do przewidywania błędów. Funkcja straty wchodzi w grę, gdy przewidywania hipotezy zmieniają się w stosunku do rzeczywistych danych. Tutaj hipoteza reprezentuje wartość przewidywaną na podstawie cechy lub zmiennej.
4. Ustalanie parametru hipotezy : parametr hipotezy jest ustalony lub ustawiony w taki sposób, aby minimalizować funkcję straty i poprawiać przewidywanie.
5. Zmniejszanie funkcji strat : funkcja strat jest minimalizowana poprzez wygenerowanie algorytmu specjalnie do minimalizacji strat w zestawie danych, co z kolei ułatwia zmianę parametrów hipotezy. Zejście gradientowe jest najczęściej używanym algorytmem minimalizacji strat. Algorytm może być również wykorzystany do innych działań po zakończeniu minimalizacji strat.
6. Analiza funkcji hipotezy : Funkcja hipotezy musi zostać przeanalizowana, ponieważ ma ona kluczowe znaczenie dla przewidywania wartości. Po przeanalizowaniu funkcji jest ona następnie testowana na danych testowych.

Przyjrzyjmy się teraz dwóm sposobom wykorzystania regresji wielowymiarowej.

1. Wielowymiarowa regresja liniowa

Wielowymiarowa regresja liniowa przypomina prostą regresję liniową, z tym wyjątkiem, że w wielowymiarowej regresji liniowej wiele zmiennych niezależnych ma udział w zmiennych zależnych, dlatego w obliczeniach stosuje się wiele współczynników.

• Służy do wyprowadzenia matematycznej zależności między wieloma zmiennymi losowymi. Wyjaśnia, ile wielu zmiennych niezależnych jest powiązanych z jedną zmienną zależną.
• Szczegóły dotyczące wielu zmiennych niezależnych są wykorzystywane do dokładnego przewidywania wpływu, jaki mają one na zmienną wynikową.
• Model wielowymiarowej regresji liniowej generuje zależność w postaci liniowej (postać linii prostej) z najlepszym przybliżeniem każdego punktu danych.
• Równanie modelu wielowymiarowej regresji liniowej to:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

gdzie dla i=n obserwacji:

Źródło

Kiedy można zastosować regresję liniową?

Model regresji liniowej może być stosowany tylko wtedy, gdy istnieją dwie zmienne ciągłe, od których jedna jest zależna, a druga niezależna.

Zmienna niezależna jest używana jako parametr do określenia wartości lub wyniku zmiennej zależnej.

2. Wielowymiarowa regresja logistyczna

Regresja logistyczna to algorytm używany do przewidywania wyniku binarnego na podstawie wielu zmiennych niezależnych. Wynik binarny ma dwie możliwości, albo scenariusz się wydarzy (reprezentowany przez 1), albo się nie wydarzy (oznaczony przez 0).

Regresja logistyczna jest wykorzystywana podczas pracy na danych binarnych, danych, których wynik (lub zmienna zależna) jest dychotomiczny.

Gdzie można zastosować regresję logistyczną?

Regresja logistyczna służy przede wszystkim do rozwiązywania problemów z klasyfikacją. Na przykład, aby upewnić się, czy wiadomość e-mail jest spamem, czy nie i czy dana transakcja jest złośliwa, czy nie. W analizie danych służy do podejmowania obliczonych decyzji w celu zminimalizowania strat i zwiększenia zysków.

Wielowymiarowa regresja logistyczna jest stosowana, gdy istnieje jedna zmienna zależna i wiele wyników. Różni się od regresji logistycznej tym, że ma więcej niż dwa możliwe wyniki.

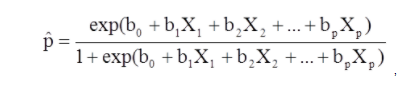
X1 do Xp są odrębnymi zmiennymi niezależnymi.

b0 do bp to współczynniki regresji

Model wielokrotnej regresji logistycznej można również zapisać w innej formie. W poniższym formularzu wynik jest oczekiwanym logiem szans, że wynik jest obecny,

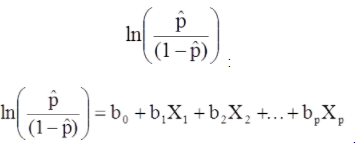
Model wielokrotnej regresji logistycznej można również zapisać w innej formie. W poniższym formularzu wynik jest oczekiwanym logiem szans, że wynik jest obecny.

Prawa strona powyższego równania przypomina równanie regresji liniowej, ale sposób wyznaczania współczynników regresji jest inny.

Założenia w modelu regresji wielowymiarowej

• Zmienne zależne i niezależne mają zależność liniową.
• Zmienne niezależne nie mają między sobą silnej korelacji.
• Obserwacje yi​ są wybierane losowo i indywidualnie z populacji.

Założenia w wielowymiarowym modelu regresji logistycznej

• Zmienna zależna jest nominalna lub porządkowa. Zmienne nominalne mają dwie lub więcej kategorii bez żadnej znaczącej organizacji. Zmienne porządkowe mogą również mieć dwie lub więcej kategorii, ale mają strukturę i mogą być uszeregowane.
• Może istnieć jedna lub wiele zmiennych niezależnych, które mogą być porządkowe, ciągłe lub nominalne. Zmienne ciągłe to takie, które mogą mieć nieskończone wartości w określonym zakresie.
• Zmienne zależne wzajemnie się wykluczają i wyczerpują.
• Zmienne niezależne nie mają między sobą silnej korelacji.

Zalety regresji wielowymiarowej

1. Regresja wielowymiarowa pomaga nam badać relacje między wieloma zmiennymi w zbiorze danych.
2. Korelacja między zmiennymi zależnymi i niezależnymi pomaga w przewidywaniu wyniku.
3. Jest to jeden z najwygodniejszych i najpopularniejszych algorytmów wykorzystywanych w uczeniu maszynowym.

Wady regresji wielowymiarowej

• Złożoność technik wielowymiarowych wymaga złożonych obliczeń matematycznych.
• Interpretacja wyników modelu regresji wielowymiarowej nie jest łatwa, ponieważ w danych wyjściowych dotyczących strat i błędów występują niespójności.
• Wielowymiarowych modeli regresji nie można zastosować do mniejszych zestawów danych; są przeznaczone do tworzenia dokładnych wyników, jeśli chodzi o większe zbiory danych.

Jeśli chcesz dowiedzieć się więcej o regresji wielowymiarowej i innych złożonych przedmiotach związanych z nauką o danych, upGrad ma właśnie dla Ciebie rozwiązanie. Nasz 18-miesięczny kurs Master of Science in Data Science z Liverpool John Moores University obejmuje ponad 500 rygorystycznych godzin nauki, 25 sesji coachingowych (odbywających się w skali 1:8) i ponad 20 sesji na żywo. upGrad oferuje również pomoc dydaktyczną 1:1 i wsparcie w zakresie poradnictwa zawodowego 360° dla studentów, aby mogli zmienić swoją karierę zawodową. Uczniowie mogą wykorzystać uczenie się peer-to-peer na globalnej platformie z ponad 40 000 płatnych uczniów i pracować nad wspólnymi projektami w sześciu specjalizacjach funkcjonalnych, aby zmaksymalizować swoje doświadczenie w nauce.