Gaussowski naiwny Bayes: co musisz wiedzieć?
Opublikowany: 2021-02-22Spis treści
Gaussowski naiwny Bayes
Naive Bayes to probabilistyczny algorytm uczenia maszynowego używany do wielu funkcji klasyfikacyjnych i oparty na twierdzeniu Bayesa. Gaussian Naive Bayes jest rozszerzeniem naiwnego Bayesa. Podczas gdy inne funkcje są używane do szacowania rozkładu danych, rozkład Gaussa lub normalny jest najprostszy do zaimplementowania, ponieważ będziesz musiał obliczyć średnią i odchylenie standardowe dla danych uczących.
Co to jest algorytm naiwnego Bayesa?
Naive Bayes to probabilistyczny algorytm uczenia maszynowego, który można wykorzystać w kilku zadaniach klasyfikacyjnych. Typowe zastosowania Naive Bayes to klasyfikacja dokumentów, filtrowanie spamu, przewidywanie i tak dalej. Algorytm ten opiera się na odkryciach Thomasa Bayesa i stąd jego nazwa.
Nazwa „Naive” jest używana, ponieważ algorytm zawiera w swoim modelu cechy, które są od siebie niezależne. Wszelkie modyfikacje wartości jednej cechy nie wpływają bezpośrednio na wartość żadnej innej cechy algorytmu. Główną zaletą algorytmu Naive Bayes jest to, że jest to prosty, ale potężny algorytm.
Opiera się na modelu probabilistycznym, w którym algorytm można łatwo zakodować, a prognozy są wykonywane szybko w czasie rzeczywistym. Dlatego ten algorytm jest typowym wyborem do rozwiązywania rzeczywistych problemów, ponieważ można go dostroić, aby natychmiast odpowiadał na żądania użytkowników. Ale zanim zagłębimy się w Naive Bayes i Gaussian Naive Bayes, musimy wiedzieć, co oznacza prawdopodobieństwo warunkowe.
Wyjaśnienie prawdopodobieństwa warunkowego
Na przykładzie możemy lepiej zrozumieć prawdopodobieństwo warunkowe. Kiedy rzucasz monetą, prawdopodobieństwo wyprzedzenia lub ogona wynosi 50%. Podobnie prawdopodobieństwo uzyskania 4, gdy rzucasz kośćmi z twarzami, wynosi 1/6 lub 0,16.
Jeśli weźmiemy talię kart, jakie jest prawdopodobieństwo uzyskania damy pod warunkiem, że jest to pik? Ponieważ warunek jest już ustawiony, że musi to być pik, mianownik lub zestaw selekcji wynosi 13. W pikach jest tylko jeden hetman, stąd prawdopodobieństwo wybrania hetmana pik wynosi 1/13 = 0,07.

Warunkowe prawdopodobieństwo zdarzenia A dane zdarzenie B oznacza prawdopodobieństwo wystąpienia zdarzenia A, biorąc pod uwagę, że zdarzenie B już zaszło. Matematycznie, warunkowe prawdopodobieństwo A przy danym B można oznaczyć jako P[A|B] = P[A AND B] / P[B].
Rozważmy trochę skomplikowany przykład. Weź szkołę liczącą w sumie 100 uczniów. Ta populacja może być podzielona na 4 kategorie - studenci, nauczyciele, mężczyźni i kobiety. Rozważ poniższą tabelę:
| Płeć żeńska | Męski | Całkowity | |
| Nauczyciel | 8 | 12 | 20 |
| Student | 32 | 48 | 80 |
| Całkowity | 40 | 50 | 100 |
Tutaj, jakie jest warunkowe prawdopodobieństwo, że pewien mieszkaniec szkoły jest Nauczycielem pod warunkiem, że jest Człowiekiem.
Aby to obliczyć, będziesz musiał przefiltrować subpopulację 60 mężczyzn i przejść do 12 nauczycieli płci męskiej.
Zatem oczekiwane prawdopodobieństwo warunkowe P[Nauczyciel | Mężczyzna] = 12/60 = 0,2
P (Nauczyciel | Mężczyzna) = P (Nauczyciel ∩ Mężczyzna) / P(Mężczyzna) = 12/60 = 0,2
Można to przedstawić jako nauczyciela(A) i mężczyznę(B) podzielone przez mężczyznę(B). Podobnie można obliczyć warunkowe prawdopodobieństwo B dla danego A. Zasadę, którą stosujemy dla Naive Bayes można wywnioskować z następujących zapisów:
P (A | B) = P (A ∩ B) / P(B)
P (B | A) = P (A ∩ B) / P(A)
Zasada Bayesa
W regule Bayesa przechodzimy od P (X | Y), które można znaleźć w uczącym zbiorze danych, aby znaleźć P (Y | X). Aby to osiągnąć, wystarczy w powyższych wzorach zamienić A i B na X i Y. W przypadku obserwacji X byłoby zmienną znaną, a Y zmienną nieznaną. Dla każdego wiersza zbioru danych musisz obliczyć prawdopodobieństwo wystąpienia Y, biorąc pod uwagę, że X już wystąpiło.
Ale co się dzieje, gdy w Y jest więcej niż 2 kategorie? Musimy obliczyć prawdopodobieństwo każdej klasy Y, aby znaleźć zwycięską klasę.
Zgodnie z regułą Bayesa przechodzimy od P (X | Y) do znalezienia P (Y | X)
Znane z danych treningowych: P (X | Y) = P (X ∩ Y) / P(Y)
P (Dowód | Wynik)
Nieznane – należy przewidzieć dla danych testowych: P (Y | X) = P (X ∩ Y) / P(X)

P (Wynik | Dowód)
Reguła Bayesa = P (Y | X) = P (X | Y) * P (Y) / P (X)
Naiwni Bayesowie
Reguła Bayesa dostarcza wzoru na prawdopodobieństwo Y przy danym warunku X. Ale w świecie rzeczywistym może być wiele zmiennych X. W przypadku niezależnych funkcji regułę Bayesa można rozszerzyć na regułę Naive Bayesa. Znaki X są od siebie niezależne. Formuła Naive Bayes jest silniejsza niż formuła Bayes
Gaussowski naiwny Bayes
Jak dotąd widzieliśmy, że X są w kategoriach, ale jak obliczyć prawdopodobieństwa, gdy X jest zmienną ciągłą? Jeśli założymy, że X ma określony rozkład, można użyć funkcji gęstości prawdopodobieństwa tego rozkładu do obliczenia prawdopodobieństwa prawdopodobieństw.
Jeśli założymy, że X są zgodne z rozkładem gaussowskim lub normalnym, musimy zastąpić gęstość prawdopodobieństwa rozkładu normalnego i nazwać go naiwnym Bayesem gaussowskim. Aby obliczyć tę formułę, potrzebujesz średniej i wariancji X.
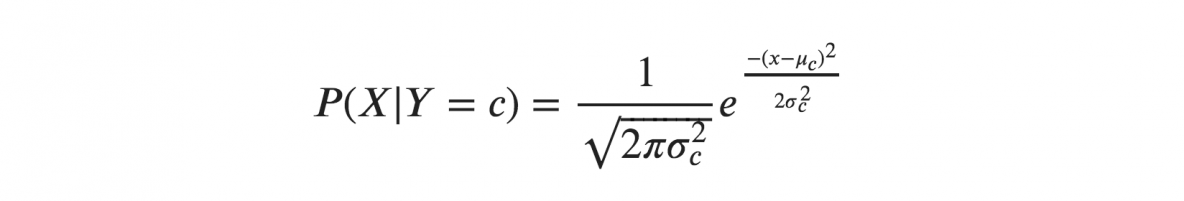
W powyższych wzorach sigma i mu to wariancja i średnia zmiennej ciągłej X obliczona dla danej klasy c Y.
Reprezentacja Bayesa naiwnego Gaussa
Powyższy wzór obliczył prawdopodobieństwa wartości wejściowych dla każdej klasy poprzez częstotliwość. Możemy obliczyć średnią i odchylenie standardowe x dla każdej klasy dla całego rozkładu.
Oznacza to, że wraz z prawdopodobieństwami dla każdej klasy musimy również przechowywać średnią i odchylenie standardowe dla każdej zmiennej wejściowej dla tej klasy.
średnia(x) = 1/n * suma(x)
gdzie n reprezentuje liczbę wystąpień, a x jest wartością zmiennej wejściowej w danych.
odchylenie standardowe(x) = sqrt(1/n * suma(xi-średnia(x)^2))
Tutaj obliczany jest pierwiastek kwadratowy ze średniej różnic każdego x i średnia x jest obliczana, gdzie n jest liczbą wystąpień, sum() jest funkcją sumy, sqrt() jest funkcją pierwiastka kwadratowego, a xi jest określoną wartością x .

Prognozy z Gaussowskim naiwnym modelem Bayesa
Funkcja gęstości prawdopodobieństwa Gaussa może być wykorzystana do dokonywania prognoz poprzez zastąpienie parametrów nową wartością wejściową zmiennej, w wyniku czego funkcja Gaussa da oszacowanie prawdopodobieństwa nowej wartości wejściowej.
Naiwny klasyfikator Bayesa
Klasyfikator Naive Bayes zakłada, że wartość jednej cechy jest niezależna od wartości jakiejkolwiek innej cechy. Klasyfikatory Naive Bayes potrzebują danych uczących, aby oszacować parametry wymagane do klasyfikacji. Ze względu na prostą konstrukcję i zastosowanie, klasyfikatory Naive Bayes mogą być odpowiednie w wielu rzeczywistych scenariuszach.
Wniosek
Klasyfikator Gaussian Naive Bayes to szybka i prosta technika klasyfikatora, która działa bardzo dobrze bez zbytniego wysiłku i z dobrym poziomem dokładności.
Jeśli chcesz dowiedzieć się więcej o sztucznej inteligencji, uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznych szkoleń, ponad 30 studiów przypadków i zadań, Status absolwentów IIIT-B, ponad 5 praktycznych praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.
Ucz się kursu ML z najlepszych światowych uniwersytetów. Zdobywaj programy Masters, Executive PGP lub Advanced Certificate Programy, aby przyspieszyć swoją karierę.
Co to jest naiwny algorytm Bayesa?
Naive bayes to klasyczny algorytm uczenia maszynowego. Naiwny bayes, wywodzący się ze statystyki, jest prostym i potężnym algorytmem. Bayes naiwny to rodzina klasyfikatorów opartych na zastosowaniu warunkowej analizy prawdopodobieństwa. W tej analizie prawdopodobieństwo warunkowe zdarzenia jest obliczane przy użyciu prawdopodobieństwa każdego z poszczególnych zdarzeń składających się na zdarzenie. Klasyfikatory bayesowskie naiwne często okazują się w praktyce niezwykle skuteczne, zwłaszcza gdy liczba wymiarów zestawu cech jest duża.
Jakie są zastosowania algorytmu naiwnego bayesa?
Naive Bayes jest używany do klasyfikacji tekstu, klasyfikacji dokumentów oraz do indeksowania dokumentów. W naiwnych bayes, każda możliwa cecha nie ma przypisanej wagi w fazie przetwarzania wstępnego, a wagi są przypisywane później podczas treningu oraz faz rozpoznawania. Podstawowym założeniem naiwnego algorytmu bayesa jest niezależność cech.
Co to jest algorytm Gaussa Naive Bayesa?
Gaussian Naive Bayes to probabilistyczny algorytm klasyfikacji oparty na zastosowaniu twierdzenia Bayesa z silnymi założeniami niezależności. W kontekście klasyfikacji niezależność odnosi się do idei, że obecność jednej wartości cechy nie wpływa na obecność innej (w przeciwieństwie do niezależności w teorii prawdopodobieństwa). Naiwność odnosi się do zastosowania założenia, że cechy przedmiotu są od siebie niezależne. W kontekście uczenia maszynowego wiadomo, że naiwne klasyfikatory Bayesa są wysoce ekspresyjne, skalowalne i dość dokładne, ale ich wydajność gwałtownie spada wraz ze wzrostem zestawu treningowego. Szereg funkcji przyczynia się do sukcesu naiwnych klasyfikatorów Bayesa. Przede wszystkim nie wymagają one dostrajania parametrów modelu klasyfikacyjnego, dobrze skalują się z rozmiarem zestawu danych uczących i z łatwością radzą sobie z funkcjami ciągłymi.
