Aktualizacja animacji CSS o krzywe ruchu

Jest animacja UI, a potem jest dobra animacja UI. Dobra animacja sprawia, że ​​mówisz „Wow!” — jest gładka, piękna i przede wszystkim naturalna, nie klockowata, sztywna czy zrobotyzowana. Jeśli często odwiedzasz Dribbble lub UpLabs, będziesz wiedział, o czym mówię.

Dalsza lektura na temat rozbijania:

• Animacje SVG i CSS z clip-path
• Praktyczne techniki animacji
• Tworzenie „odręcznie rysowanych” animacji za pomocą SVG
• Nowy interfejs API animacji sieciowej

Przy tak wielu niesamowitych projektantach tworzących tak piękne animacje, każdy programista naturalnie chciałby odtworzyć je we własnych projektach. Teraz CSS zapewnia pewne ustawienia wstępne dla transition-timing-function , takie jak ease-in , ease-out i ease-in-out , które dodają pewien poziom płynności i realizmu, ale są one bardzo ogólne, prawda? Jak nudne byłoby, gdyby każda animacja w sieci miała te same trzy funkcje czasowe?

Jedną z właściwości funkcji transition-timing-function jest cubic-bezier(n1, n2, n3, n4) , w której możesz przekazać cztery liczby, aby stworzyć swoją własną funkcję pomiaru czasu. Pod koniec tego artykułu będziesz dokładnie wiedział, co oznaczają te cztery liczby — ale uwierz mi, wymyślenie czterech liczb, aby uchwycić przejście, które wyobrażasz sobie w swojej głowie, nie jest wcale łatwe. Ale dzięki cubic-bezier i Cezarowi nie musisz. Te narzędzia wprowadzają krzywe ruchu do sieci.

Krzywe ruchu są używane głównie przez animatorów (na przykład w programie Adobe After Effects) do tworzenia zaawansowanych, realistycznych animacji. Dzięki cubic-bezier i Cezarowi możesz po prostu manipulować kształtem krzywej, a te cztery liczby ( n1, n2, n3, n4 ) zostaną wypełnione za Ciebie, co jest absolutnie wspaniałe! Aby jednak jak najlepiej wykorzystać i wykorzystać krzywe ruchu, musisz zrozumieć, jak one działają, i właśnie to zrobimy w tym artykule. Zaczynajmy.

Zrozumienie krzywych ruchu

Krzywa ruchu to nic innego jak wykres pomiędzy dowolną właściwością dającą się animować a czasem. Krzywa ruchu określa, w jaki sposób prędkość animacji uruchomionej pod jej wpływem zmienia się w czasie.

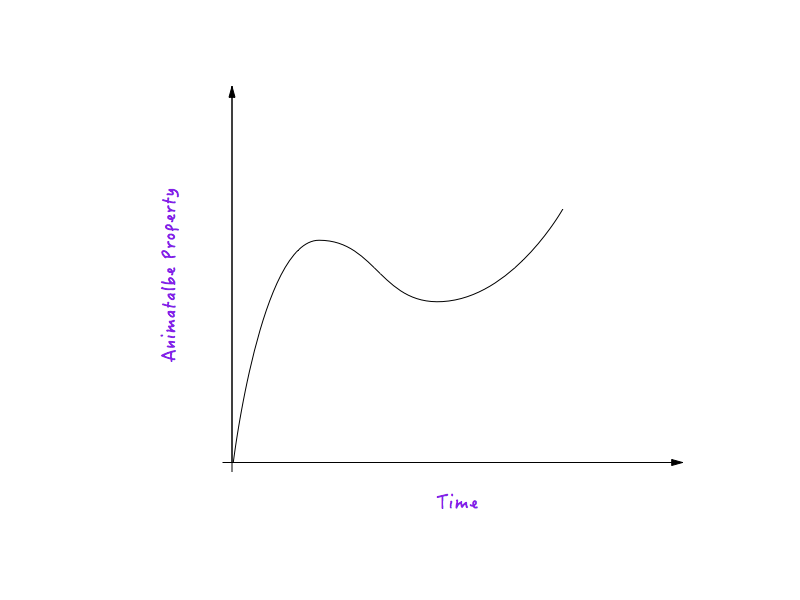
Weźmy odległość ( translateX ) jako przykład właściwości, którą można animować. (Wyjaśnienie jest prawdziwe dla każdej innej właściwości, którą można animować).

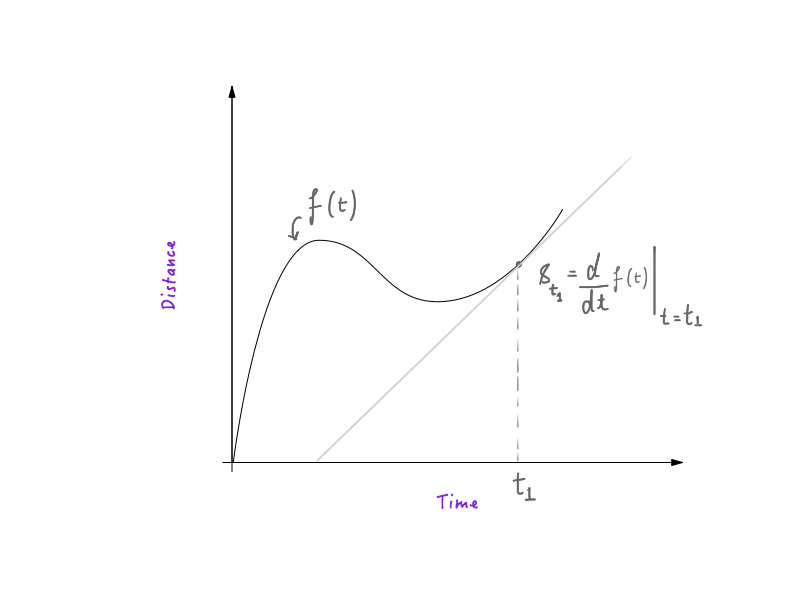
Jeśli masz jakieś doświadczenie z fizyką i podstawowymi obliczeniami, wiesz, że rozszyfrowanie prędkości z wykresu odległość-czas jest bardzo proste. Pierwszą pochodną odległości w funkcji czasu , względem czasu , jest prędkość, co oznacza, że ​​obiekt poruszający się po krzywej odległość-czas miałby większą prędkość w miejscach, gdzie krzywa jest stroma i niższa w miejscach, gdzie krzywa jest bardziej płaska . Jeśli wiesz, jak to działa, świetnie! Wszystko gotowe i możesz przejść do następnej sekcji.

Teraz zdaję sobie sprawę, że projektowanie i rozwój to bardzo zróżnicowana dziedzina i nie każdy ma takie samo doświadczenie. Być może dwa powyższe akapity były dla ciebie żargonem. Nie martw się. Będziemy kontynuować i rozumieć żargon.

Rozważ czerwone pole poniżej. Zdobądźmy tu mały szelest i nazwijmy czerwone pudełko „Boxy”; łatwiej będzie odnieść się do tego w ten sposób. W porządku, więc Boxy będzie przesuwał się od jednej krawędzi ekranu do drugiej w sposób liniowy, a my przeanalizujemy jego ruch.

Jedno z ustawień funkcji transition-timing-function jest linear . Aby Boxy się poruszał, wystarczy dodać następującą klasę.

 .moveForward { transform: translateX(1000px); }

Aby kontrolować animację, ustawimy właściwość transition dla Boxy w następujący sposób:

 #boxy { width: 200px; height: 200px; background: red; transition-property: transform; transition-duration: 1s; transition-timing-function: linear; }

To bardzo szczegółowy sposób określania transition . W rzeczywistości prawie zawsze znajdziesz transition napisane w skróconej formie:

 #boxy { width: 200px; height: 200px; background: red; transition: transform 1s linear; }

Zobaczmy, jak odchodzi.

Roboty, prawda? Można powiedzieć, że ten ruch wydaje się robotem, ponieważ jest liniowy, co jest całkowicie prawdopodobną odpowiedzią. Ale czy mógłbyś wyjaśnić dlaczego? Widzimy, że ustawienie linear skutkuje ruchem robota, ale co dokładnie dzieje się za sceną? Właśnie to dowiemy się najpierw; przejdziemy do wnętrzności i zrozumiemy, dlaczego ten ruch wydaje się robotyczny, blokowy i nienaturalny.

Zacznijmy od narysowania wykresu ruchu Boxy'ego, aby zobaczyć, czy możemy uzyskać pewien wgląd. Nasz wykres będzie miał dwie osie, pierwszą będzie odległość, a drugą czas. Boxy pokonuje całkowitą odległość 1000 pikseli (odległość) w ciągu 1 sekundy (czas). Teraz nie bój się matematyki poniżej — to bardzo proste.

Oto nasz bardzo prosty wykres z wymienionymi osiami.

W tej chwili jest pusty. Wypełnijmy go danymi.

Na początek wiemy, że w 0 sekundzie, kiedy animacja jeszcze się nie zaczęła, Boxy znajduje się w swojej początkowej pozycji (0 pikseli). A po upływie 1 sekundy Boxy przebył łącznie 1000 pikseli, lądując na przeciwległej krawędzi ekranu.

Wykreślmy te dane na wykresie.

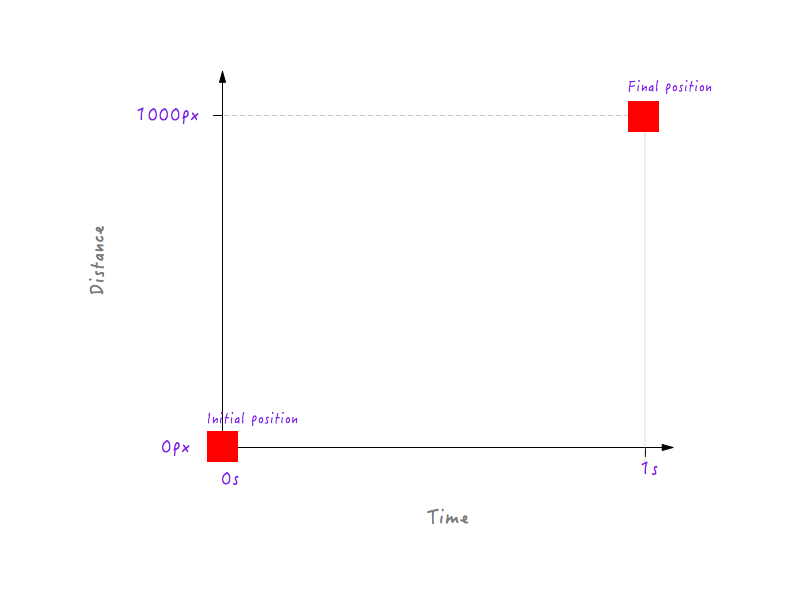
Na razie w porządku. Ale dwa punkty danych to za mało — potrzebujemy więcej. Poniższy rysunek pokazuje pozycje Boxy'ego w różnych momentach (wszystko dzięki mojej szybkiej kamerze).

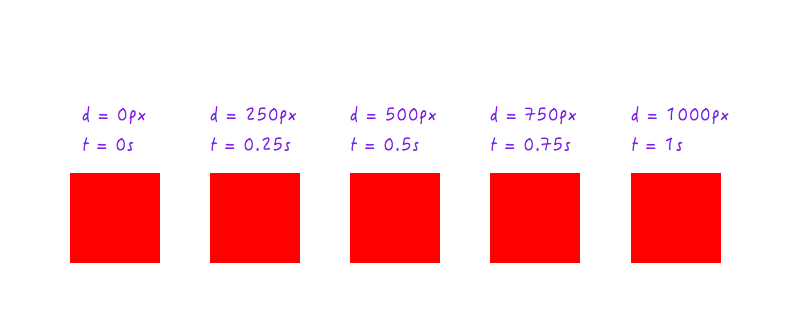
Dodajmy te dane do naszego wykresu.

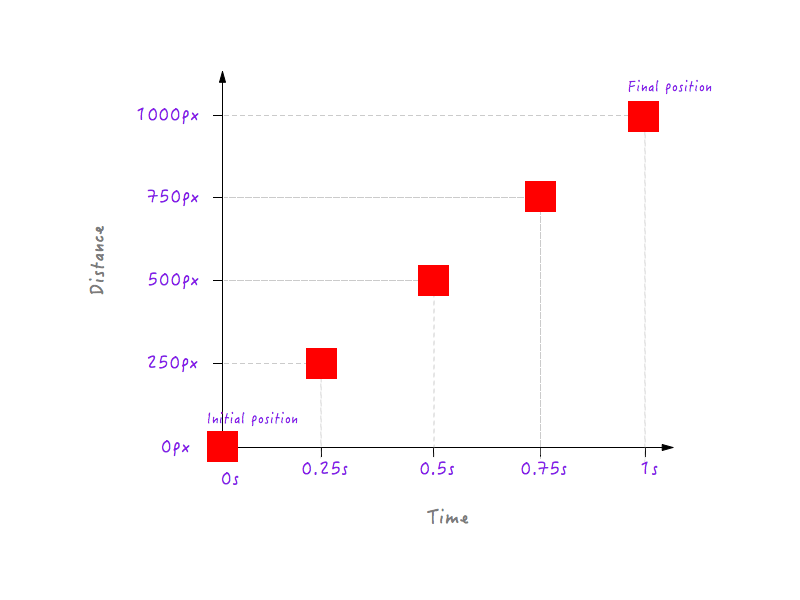
Możesz oczywiście mieć o wiele więcej punktów danych dla różnych czasów (na przykład 0,375 sekundy, 0,6 sekundy itd.), ale to, co mamy, wystarczy, aby uzupełnić nasz wykres. Łącząc wszystkie punkty, zakończyliśmy wykres. Piątka!

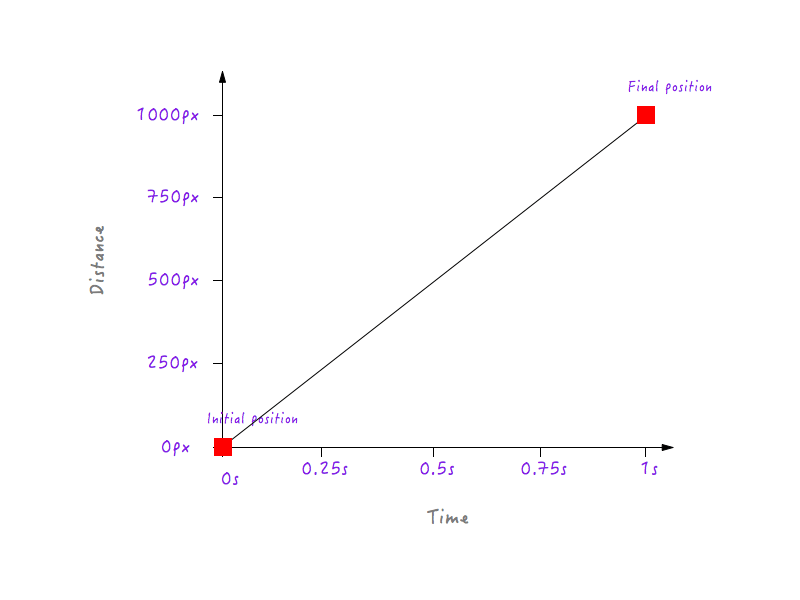
Fajnie, ale co nam to mówi? Pamiętasz, że rozpoczęliśmy nasze dochodzenie w celu zrozumienia, dlaczego ruch liniowy Boxy wydaje się nienaturalny i zautomatyzowany? Na pierwszy rzut oka ten wykres, który właśnie stworzyliśmy, nic nam o tym nie mówi. Musimy zejść głębiej.

Pamiętaj o wykresie i porozmawiajmy przez chwilę o prędkości. Wiem, że wiesz, czym jest prędkość — chciałbym to ująć w kategoriach matematycznych. Jak to się mówi, wzór na prędkość jest następujący:

Dlatego jeśli samochód pokonuje dystans 100 kilometrów w ciągu 1 godziny, mówimy, że jego prędkość wynosi 100 kilometrów na godzinę.

Jeśli samochód podwoi prędkość, to w tym samym odstępie czasu (1 godzina) zacznie pokonywać dwukrotność dystansu (200 kilometrów), czyli pokonuje pierwotną odległość 100 kilometrów w czasie o połowę krótszym (0,5 godziny). . Ma sens?

Podobnie, jeśli samochód zmniejszyłby prędkość o połowę (czyli spowolnił o połowę), zacząłby pokonywać dystans 50 kilometrów w tym samym odstępie (1 godzina) lub innymi słowy, przejechałby pierwotną odległość 100 kilometrów w dwa razy więcej czasu (2 godziny).

Świetnie! Pomijając to, wróćmy do miejsca, w którym skończyliśmy. Próbowaliśmy dowiedzieć się, w jaki sposób wykres między odległością a czasem może pomóc nam zrozumieć, dlaczego ruch liniowy Boxy wydaje się robotem.

Hej, poczekaj chwilę! Mamy wykres między odległością a czasem, a prędkość można obliczyć na podstawie odległości i czasu, prawda? Spróbujmy obliczyć prędkość Boxy'ego w różnych odstępach czasu.

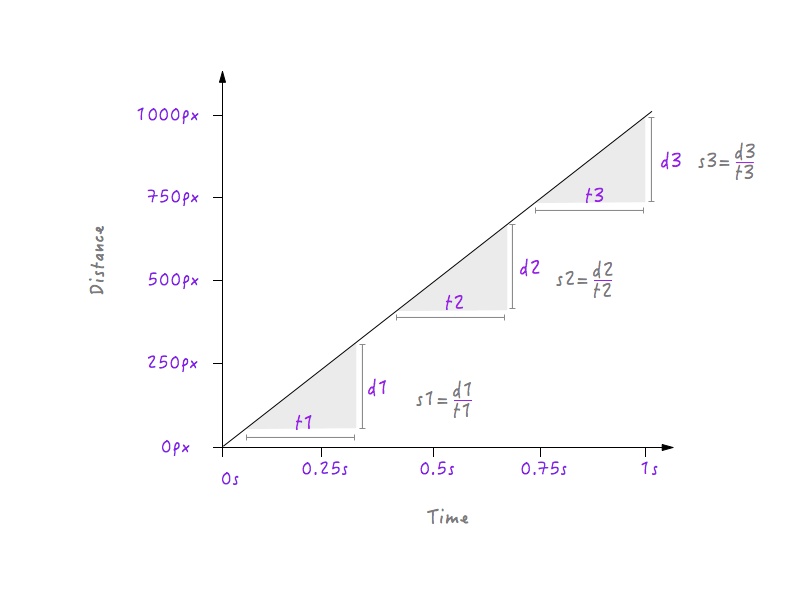
Tutaj wybrałem trzy różne przedziały czasowe: jeden w pobliżu startu, jeden w środku i jeden na końcu w pobliżu pozycji końcowej. Jak widać, we wszystkich trzech odstępach Boxy ma dokładnie taką samą prędkość (s1 = s2 = s3) wynoszącą 1000 pikseli na sekundę; to znaczy, bez względu na to, jaki interwał wybierzesz na powyższym wykresie, Boxy będzie poruszał się z prędkością 1000 pikseli na sekundę. Czy to nie dziwne? Rzeczy w prawdziwym życiu nie poruszają się ze stałą prędkością; zaczynają powoli, stopniowo zwiększają swoją prędkość, poruszają się przez chwilę, a następnie zwalniają przed zatrzymaniem, ale Boxy nagle zaczyna z prędkością 1000 pikseli na sekundę, poruszając się z tą samą prędkością i nagle zatrzymując się dokładnie z tą samą prędkością. Dlatego ruch Boxy'ego wydaje się robotyczny i nienaturalny. Będziemy musieli zmienić nasz wykres, aby to naprawić. Ale zanim zagłębimy się w temat, musimy wiedzieć, jak zmiany prędkości wpłyną na wykres między odległością a czasem. Gotowy? Bedzie fajnię.

Podwójmy prędkość Boxy'ego i zobaczmy, jak wygląd wykresu zmienia się w odpowiedzi. Oryginalna prędkość Boxy'ego, jak obliczyliśmy powyżej, wynosi 1000 pikseli na sekundę. Ponieważ podwoiliśmy prędkość, Boxy będzie teraz w stanie pokonać odległość 1000 pikseli w czasie o połowę krótszym — czyli w 0,5 sekundy. Umieśćmy to na wykresie.

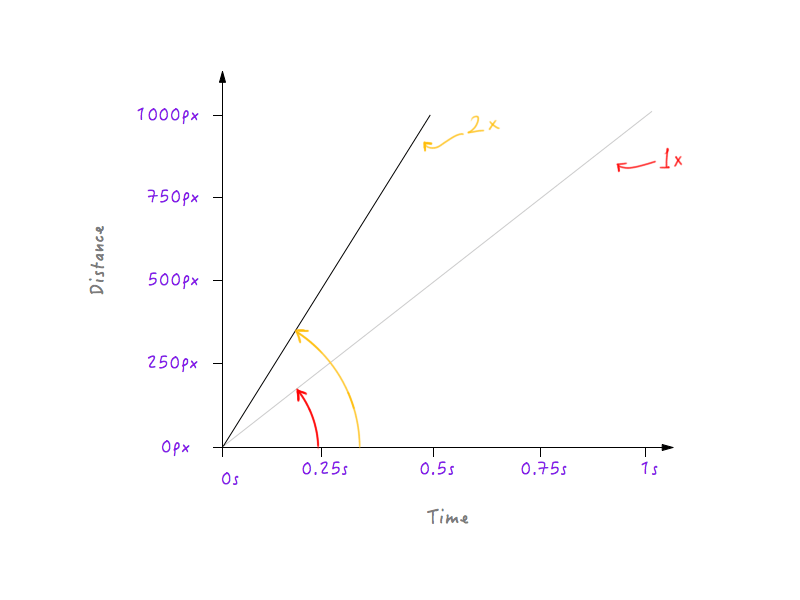
Co jeśli potroimy prędkość? Boxy obejmuje teraz 1000 pikseli w jednej trzeciej czasu (jedna trzecia sekundy).

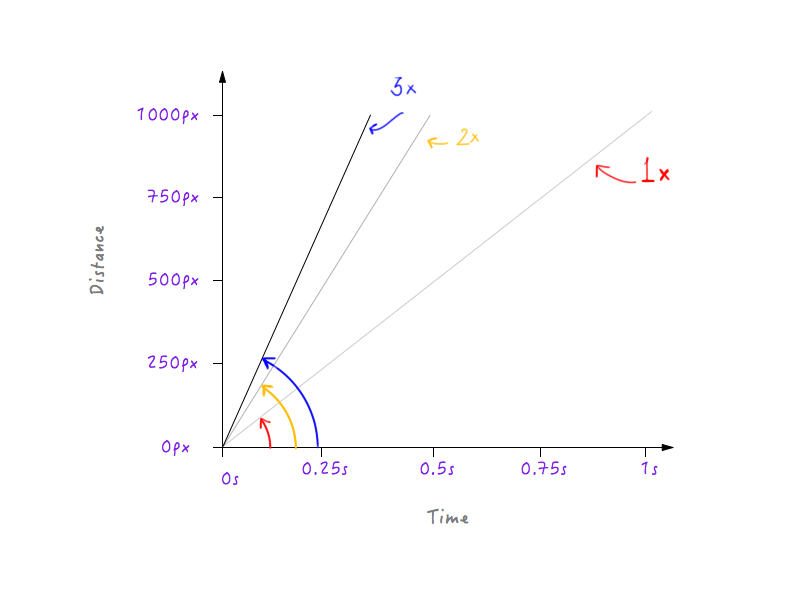
Hmm, zauważyłeś coś? Zauważ, że gdy wykres się zmienia, kąt, jaki tworzy linia z osią czasu, zwiększa się wraz ze wzrostem prędkości.

W porządku, chodźmy i zmniejszmy o połowę prędkość Boxy'ego. Zmniejszenie prędkości o połowę oznacza, że ​​Boxy będzie w stanie pokryć tylko 500 pikseli (połowa oryginalnej odległości) w ciągu 1 sekundy. Umieśćmy to na wykresie.

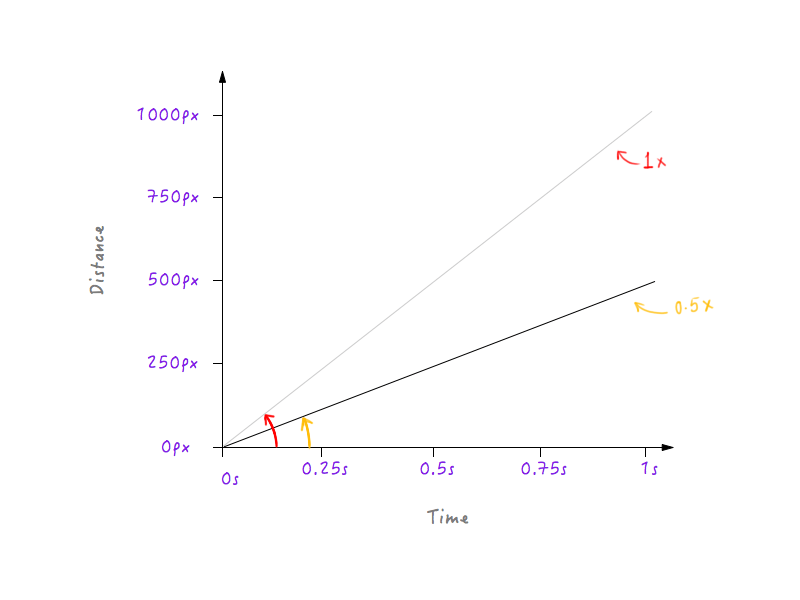
Zwolnijmy Boxy'ego trochę bardziej, zwiększając prędkość o jedną trzecią oryginału. Boxy będzie w stanie pokonać jedną trzecią pierwotnej odległości w ciągu 1 sekundy.

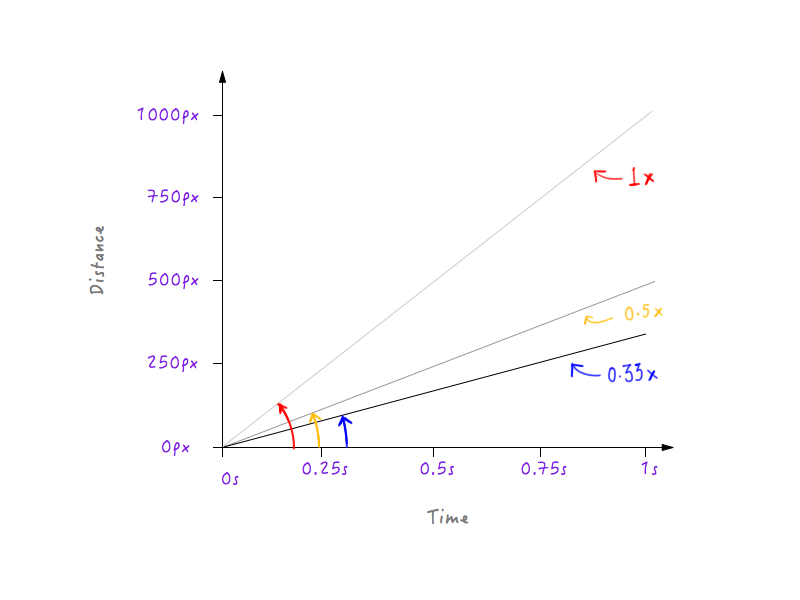
Widzisz wzór? Linia staje się coraz bardziej stroma, gdy zwiększamy prędkość Boxy'ego, i zaczyna się spłaszczać, gdy zwalniamy Boxy'ego.

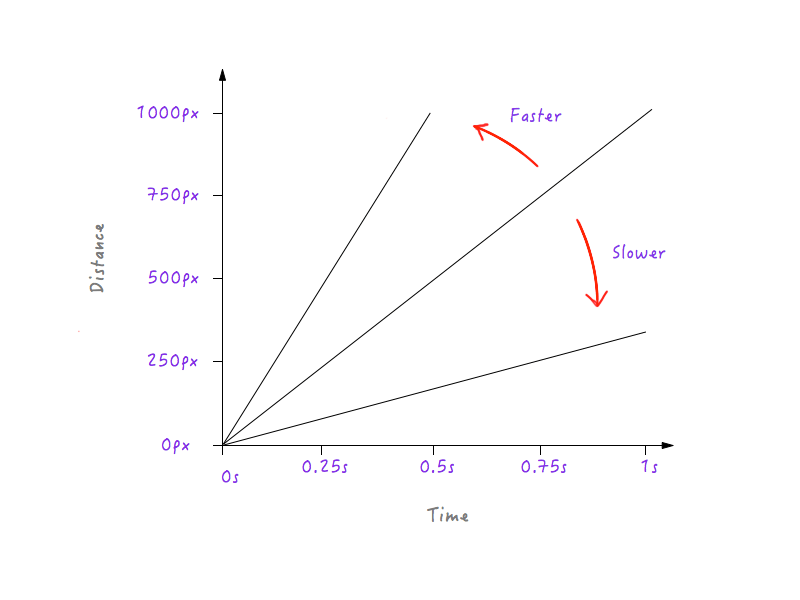
Ma to sens, ponieważ w przypadku bardziej stromej linii niewielki postęp w czasie powoduje znacznie większą zmianę odległości, co oznacza większą prędkość.

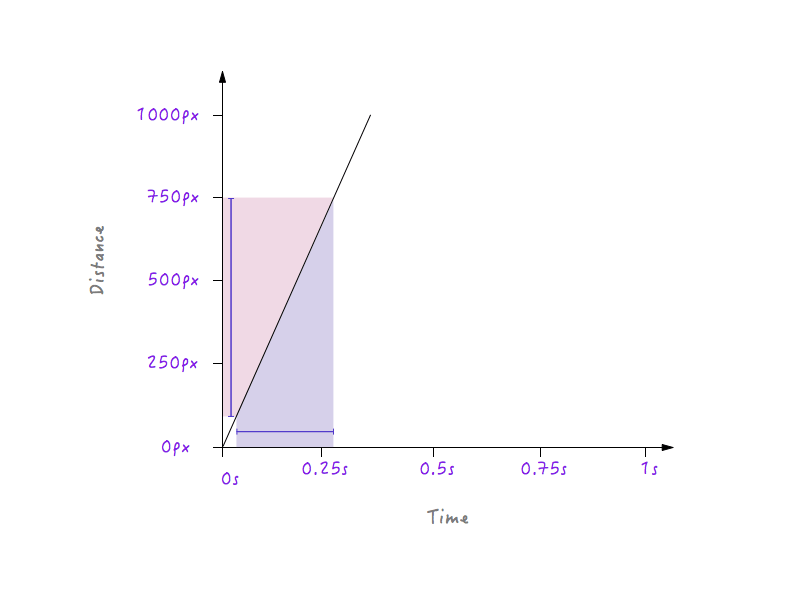
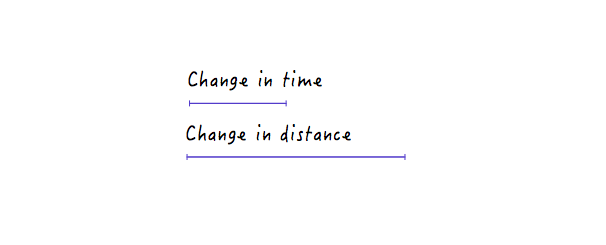
Z drugiej strony, w przypadku linii, która jest mniej stroma, duża zmiana w czasie powoduje tylko niewielką zmianę odległości, co oznacza niższą prędkość.

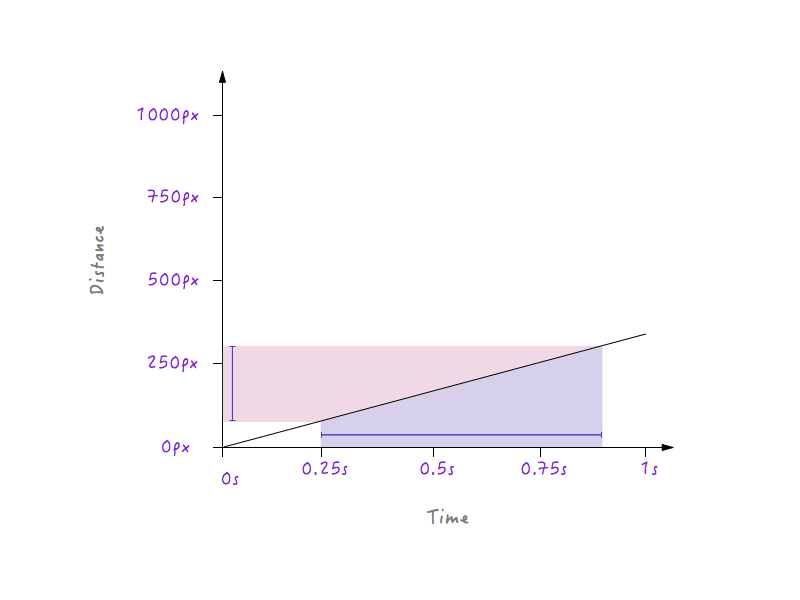
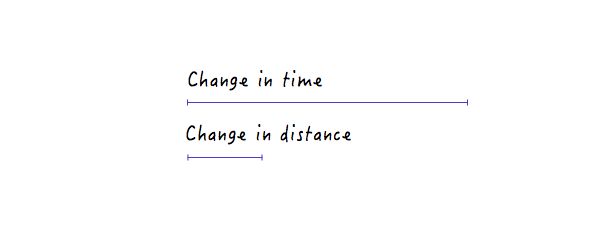
Przy wszystkich wprowadzonych przez nas zmianach Boxy wciąż porusza się liniowo, tylko z różnymi prędkościami. Jednak dzięki naszej nowo zdobytej wiedzy o tym, jak zmiany odległości w zależności od czasu mogą wpływać na prędkość, możemy eksperymentować i rysować wykres, który sprawi, że Boxy porusza się w sposób, który wygląda naturalnie i realistycznie.

Zróbmy to krok po kroku. Po pierwsze, rzeczy w prawdziwym życiu zaczynają się powoli i powoli nabierają tempa. Więc zróbmy to.

We wszystkich iteracjach wykresu pokazanych poniżej zauważysz, że punkty w przeciwległych rogach pozostają stałe. Dzieje się tak, ponieważ nie zmieniamy czasu trwania animacji ani odległości, jaką pokonuje Boxy.

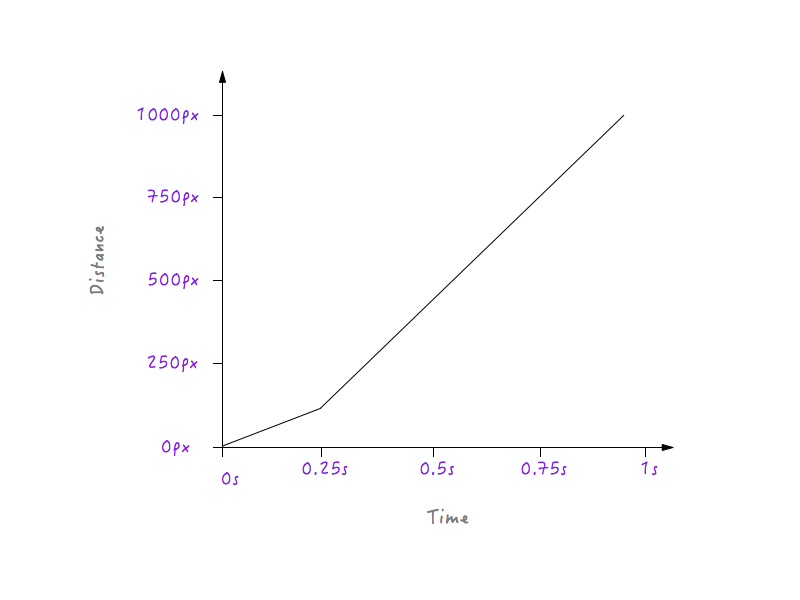
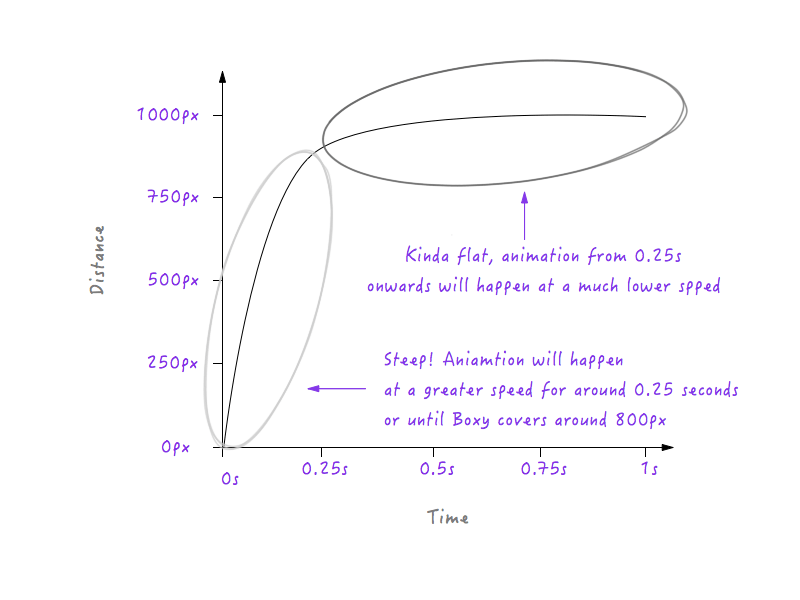
Jeśli Boxy będzie podążał za powyższym wykresem, będzie się poruszał wolniej przez 0,25 sekundy, ponieważ linia jest mniej stroma, zaczynając od 0 do 0,25 sekundy, a następnie nagle przełączy się na wyższą prędkość po 0,25 sekundy (powodem jest to, że linia na wykresie staje się bardziej stroma po 0,25 sekundy). Musimy jednak wygładzić to przejście; nie chcemy żadnych narożników — w końcu nazywa się to krzywą ruchu. Zamieńmy ten róg w krzywą.

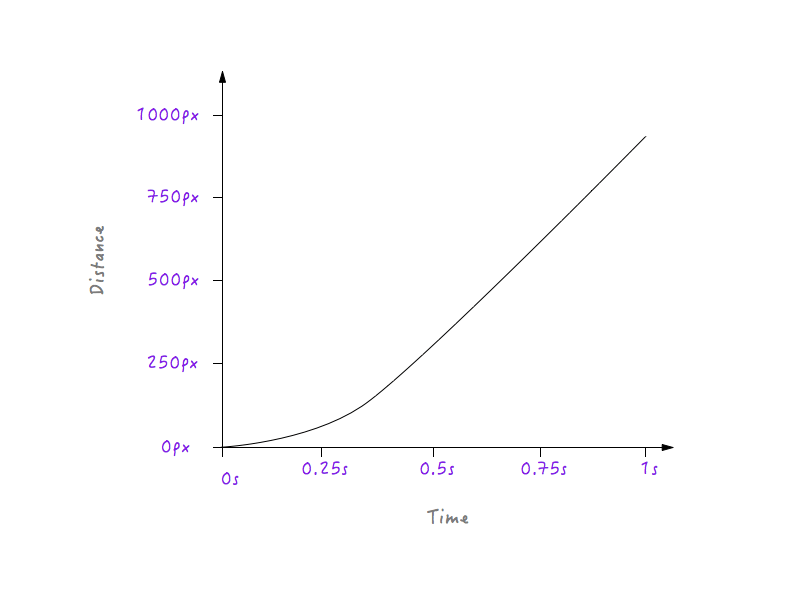
Zwróć uwagę na płynne przejście, które Boxy przechodzi od spoczynku do stopniowego zwiększania prędkości.

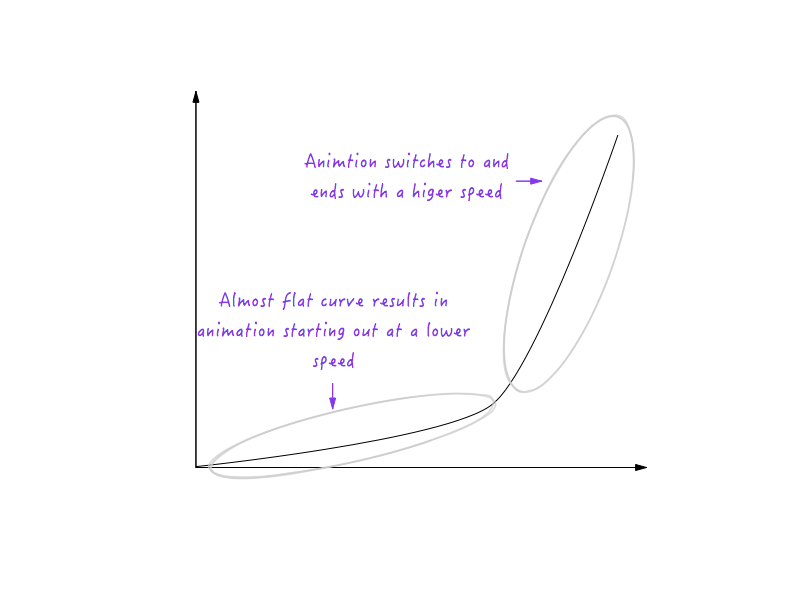
Dobry! Następnie obiekty w prawdziwym życiu stopniowo zwalniają, zanim się zatrzymają. Zmieńmy wykres, aby tak się stało. Ponownie wybierzemy moment, po którym chcielibyśmy, aby Boxy zaczął zwalniać. Co powiesz na około 0,6 sekundy? Tutaj już wygładziłem róg przejścia w krzywą.

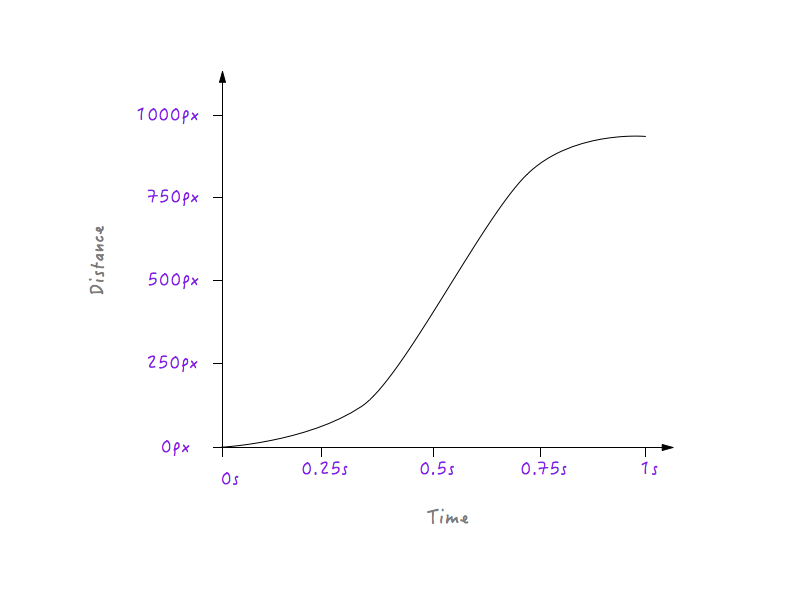
Spójrz na Boxy go! O wiele bardziej naturalny, prawda?

Krzywa, którą narysowaliśmy w miejscu narożnika, jest w rzeczywistości zbiorem wielu małych odcinków linii; a jak już wiesz, im bardziej stroma linia na wykresie, tym wyższa prędkość, a im bardziej płaska linia, tym wolniejsza prędkość. Zwróć uwagę, jak w lewej części obrazu segmenty linii tworzące krzywą stają się coraz bardziej strome, co powoduje stopniowy wzrost prędkości i stopniowo spłaszcza się po prawej stronie, powodując stopniowe zmniejszanie się prędkości?

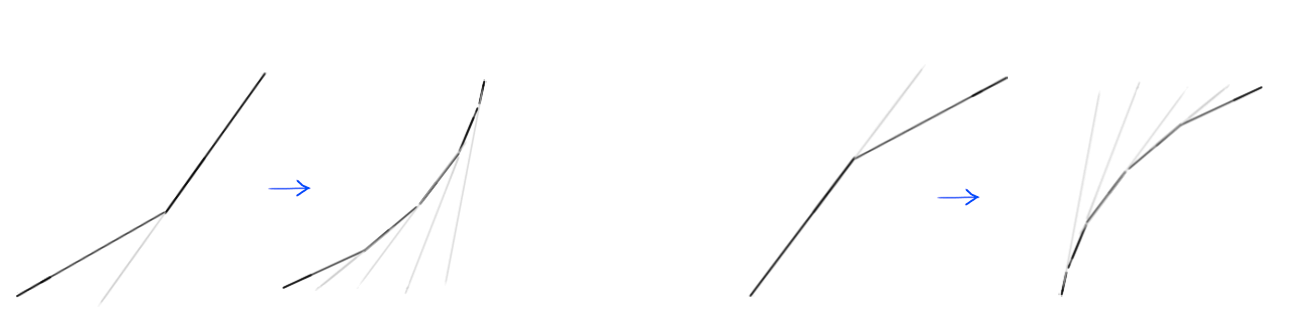
Mając całą tę wiedzę, zrozumienie krzywych ruchu staje się znacznie łatwiejsze. Spójrzmy na kilka przykładów.

Korzystanie z krzywych ruchu w animacji interfejsu użytkownika

Następnym razem, gdy będziesz musiał animować element interfejsu, będziesz miał do dyspozycji moc krzywych ruchu. Niezależnie od tego, czy jest to wysuwany pasek, okno modalne, czy menu rozwijane, dodanie odpowiedniej ilości animacji i sprawienie, by wyglądała gładko i naturalnie, znacznie poprawi jakość interfejsu użytkownika. Sprawi to, że interfejs użytkownika będzie po prostu przyjemny . Skorzystaj z wysuwanego menu poniżej:

Kliknięcie menu hamburgera powoduje wyświetlenie menu od lewej, ale animacja wydaje się blokowa. Linia 51 CSS pokazuje, że animacja ma transition-timing-function ustawioną na linear . Możemy to poprawić. Przejdźmy do sześciennego Beziera i stwórzmy niestandardową funkcję pomiaru czasu.

Jeśli to czytasz, możesz bezpiecznie założyć, że jesteś projektantem, programistą lub obydwoma, a zatem nieobce Ci są sześcienne krzywe Beziera; istnieje duża szansa, że ​​spotkałeś się z nimi przynajmniej raz. Krzywe Beziera są cudem. Są używane głównie w grafice komputerowej do rysowania kształtów i są używane w narzędziach takich jak Sketch i Adobe Illustrator do rysowania grafiki wektorowej. Powodem, dla którego sześcienne krzywe Beziera są tak popularne, jest to, że są tak łatwe w użyciu: po prostu zmodyfikuj położenie czterech różnych punktów i utwórz krzywą, której potrzebujesz.

Ponieważ zawsze znamy stan początkowy i końcowy animowanego obiektu, możemy ustalić dwa punkty. Pozostają tylko dwa punkty, których pozycje musimy zmienić. Dwa stałe punkty nazywane są punktami kontrolnymi, a pozostałe dwa są punktami kontrolnymi.

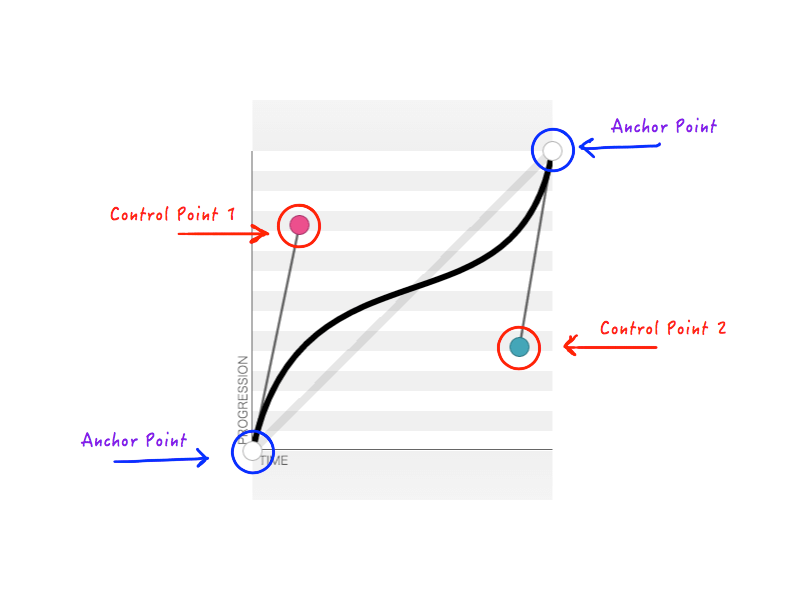
Jak pamiętasz, cubic-bezier akceptuje cztery liczby ( n1, n2, n3, n4 ) podczas tworzenia niestandardowej transition-timing-function . Te cztery liczby reprezentują tylko pozycje dwóch punktów kontrolnych: n1, n2 reprezentuje współrzędne xiy pierwszego punktu kontrolnego, a n3, n4 reprezentuje współrzędne drugiego punktu kontrolnego. Ponieważ zmiana pozycji punktów kontrolnych zmieni kształt krzywej, a co za tym idzie, całą naszą animację, wynik jest taki sam, gdy którykolwiek lub wszystkie z n1, n2, n3, n4 zostaną zmodyfikowane. Na przykład poniższy rysunek przedstawia cubic-bezier(.14, .78, .89, .35) :

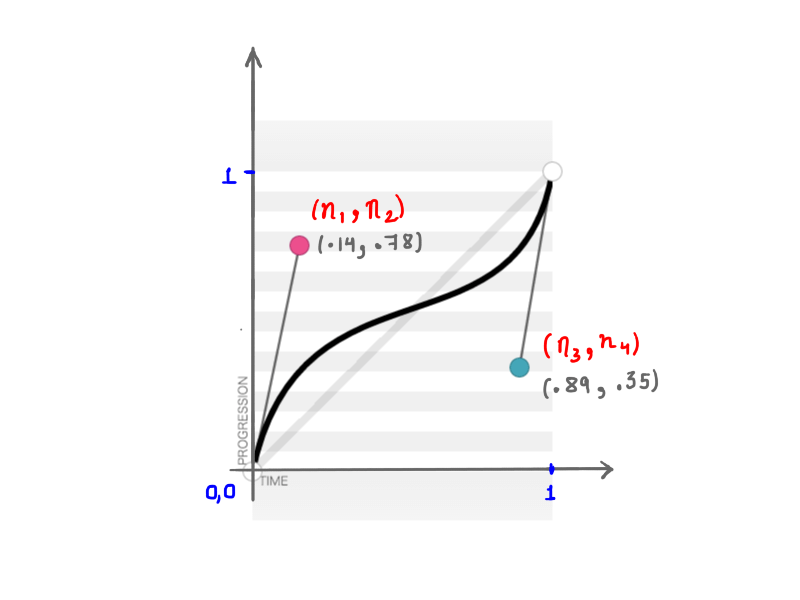
Matematyka kryjąca się za tymi pozornie prostymi krzywymi jest fascynująca.

W porządku, w porządku, wróćmy do tego, do czego zmierzaliśmy z sześciennym Bezierem: tworzenie niestandardowej transition-timing-function . Chcę animacji, w której menu wsuwa się bardzo szybko, a potem wdzięcznie zwalnia i kończy:

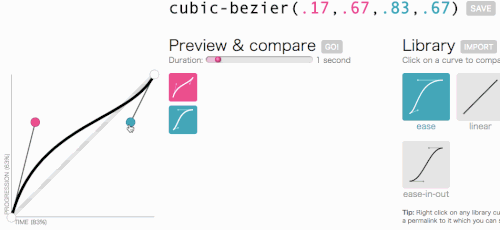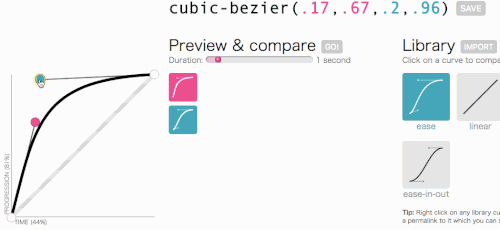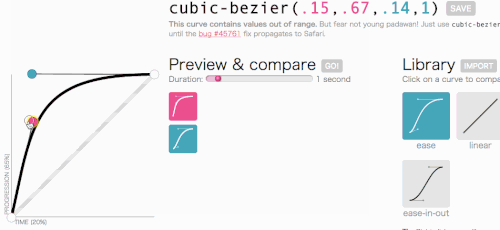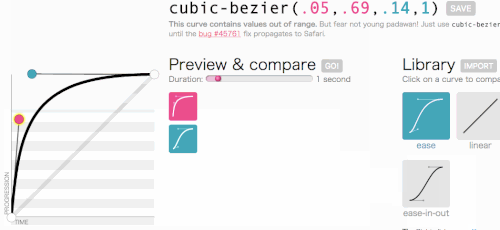
To wygląda dobrze. Animacja zacznie się szybko, a następnie zwolni, zamiast poruszać się ze stałą prędkością przez cały czas. Po prostu cubic-bezier(.05, .69, .14, 1) z góry strony i zastąpię linear .

Zobacz różnicę? Druga iteracja wydaje się znacznie bardziej naturalna i atrakcyjna. Wyobraź sobie, że każda animacja w twoim interfejsie użytkownika przebiega zgodnie z naturalną funkcją synchronizacji. Jak wspaniale by to było?

Jak widzieliśmy, krzywe ruchu wcale nie są trudne. Są bardzo łatwe do zrozumienia i użycia. Dzięki nim możesz przenieść swój interfejs użytkownika na wyższy poziom.

Mam nadzieję, że nauczyłeś się, jak działają krzywe ruchu. Jeśli przechodziłeś przez wiele prób i błędów, aby krzywe ruchu działały tak, jak chcesz, lub jeśli w ogóle ich nie używałeś, powinieneś teraz swobodnie naginać je do swojej woli i tworzyć piękne animacje. Bo przecież animacja ma znaczenie.